Сущность метода наименьших квадратов

Стр 1 из 3Следующая ⇒

Социально-экономический ракультет

Методическая разработка

для выполнения котрольного задания №1

по теме «Изучение взаимосвязей социально-экономических явлений» методом парного регрессионного анализа

(дисциплина «Статистика»)

Составитель: к.э.н. Шихалёв А.М.

Казань – 2010

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

В результате усвоения учебного материала студент должен знать:

1. Содержание постановки задачи аппроксимации исходных данных видами парных зависимостей.

2. Сущность метода наименьших квадратов (МНК) как средства аппроксимации исходных эмпирических данных в виде функциональных парных зависимостей, где одна из переменных занимает место аргумента, а другая – его функции.

3. Содержание интерпретации параметров парной линейной регрессии – свободного члена линейного уравнения, коэффициента регрессии, коэффициента линейной корреляции, а также экстраполяционные возможности полученного уравнения регрессии.

4. Механизм формирования «нулевых гипотез» и средств их верификации при поверке предположения о наличии и тесноты связи между функцией и аргументом с обеспечением стандартных требований точности аппроксимации.

В процессе выполнения данной работы студент должен выработать умения в применении МНК к парной линейной зависимости на основе конкретной эмпирической информации с получением значений параметров парной регрессии, в проверке правильности собственных расчетов полученных значений свободного члена и коэффициента регрессии, поверки гипотезы о наличии и тесноты связи значений функции и аргумента с заданной точностью, в построении экстраполяционного прогноза.

Кроме того, студент должен иметь навыки в проведении конкретных математических расчетов и интерпретации полученных результатов в виде последовательных суждений и умозаключений на неформализованном (вербальном) уровне на основе изученных по данной теме понятий.

Методическая разработка по структуре включает в себя общие положения (напоминание ранее изученного материала) и материалы по теме.

РЕГРЕССИОННЫЙ АНАЛИЗ

Общие положения

Изучение корреляционных зависимостей основывается на исследовании таких связей между переменными, при которых значения одной переменной, которая принимается исследователем за зависимую переменную «в среднем» изменяются в зависимости от того, какие значения принимает другая переменная (признак-фактор), рассматриваемая как причина по отношению к зависимой переменной.

Следовательно, первой и основной задачей регрессионного анализа является определение типа функции, с помощью которой характеризуется зависимость между признаками. Причем теоретическая линия регрессии должна расположиться относительно эмпирической, как правило, ломаной кривой, построенной на точках корреляционного поля так, чтобы сумма отклонений точек поля корреляции от соответствующих точек теоретической линии равнялась нулю, а сумма квадратов этих отклонений была бы минимальной величиной.

Таким образом, методологический аппарат регрессионного анализа так или иначе связан с анализом функций на экстремум. Рассмотрим пример из школьного курса (или из курса математического анализа) анализ функции вида y=f(x), где традиционно х принимается нами в качестве известной величины, y – неизвестной, а вид функции считается известным.

Пример анализа функции на экстремум рассмотрим для наиболее наглядной для такого случая функции – параболической. Перед нами в данном случае стоят две задачи: определить аналитическим путем, есть ли у функции экстремум (максимум или минимум); определить, что же именно – максимум или минимум. Пусть вид функции представлен так (1) В общем виде, где а = 1, а b = 3:

y = f(x) = a + (x - b)² = 1 + (x - 3)² . (1)

Для лучшей наглядности визуализируем содержание (1), для чего последовательно зададимся некоторыми значениями х, по формуле (1) найдем соответствующие значения y и занесем их в рабочую таблицу 1.

Таблица 1

Рабочая таблица

№	Х	Y
1 2 3 4 5	1,0 2,0 3,0 4,0 5,0	5,0 2,0 1,0 2,0 5,0

Данные табл. 1 представим графически на рис. 1.

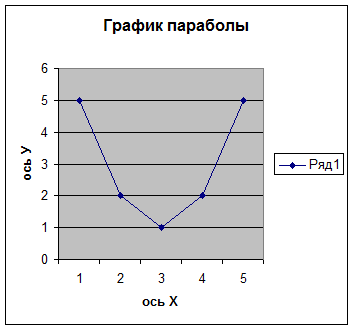Рис. 1. График функции, исследуемой на экстремум

Из рис. 1 видно, что, во-первых, экстремальное значение функции наблюдается при х=3 и что значение функции при этом – минимальное, то есть у=1. При всех остальных значениях х значения функции у будут больше, чем 1.

А теперь сделаем то же самое аналитически. Для этого формулу (1) необходимо продифференцировать, иначе говоря, найти первую производную по х

y_х^Œ = [1 + (x – 3)²]_х^Œ

dy d d

— = — [1 + (x – 3)²] = 0 + 2 (x - 3)² — (x – 3) = 2 (x – 3) = 2x – 6 (2)

dx dx dx

Для того, чтобы установить, является ли функция экстремальной, полученное выражение (2) достаточно приравнять к нулю:

2х – 6 = 0 (3)

В формуле (3) имеем одно уравнение, линейное по отношению к аргументу х и одно неизвестное. Из (3) находим х = 3 (что видно и из содержания табл. 1). Подставляя х = 1 в выражение (1), получим: у = 1.

Далее следует установить, является ли значение у = 1 для функции (1) максимальным или минимальным по известному правилу: если вторая производная от выражение (2) будет отрицательным, то функция (1) достигает в точке х = 3 свое максимальное значение; если же положительным, то функция (1) достигает в той же экстремальной точке минимальное значение.

— (2x – 6) = 2 > 0 (4)

Из выражения (4) видно, что функция у при значении х = 3 достигает своего минимального значения.

Следовательно, располагая только лишь видом функции, даже не визуализируя ее, можно определить ее экстремальное значение и установить его характер (рассмотрение возможного вопроса о единственности экстремума выходит за рамки данного рассмотрения). Важно, что здесь мы рассматриваем переменную х в качестве аргумента, значения коэффициентов а и b и их взаимосвязь полагаем известными. Задаваясь значениями х, получаем значения функции у.

Однако часто в статистике бывает наоборот: х и у известны, но неизвестны значения коэффициентов а и b.

Решением задач в такой постановке и занимается регрессионный анализ. Если переменных всего две, одна из которых подразумевается аргументом, а другая – функцией, что определяется на этапе предшествующего вычислениям в рамках так называемого концептуального (неформализованного) анализа, то аппарат определения неизвестных коэффициентов носит названия парной регрессии или задачей аппроксимации. Если аргументов более одного, то подобная задача решается в терминах множественной регрессии.

Рассмотрим механизм парной регрессии, широко используемый в социально-экономических исследованиях.

Парная регрессия

При проведении социально-экономических исследований часто приходится иметь дело со взаимосвязанными показателями. Изучить, насколько изменение одного показателя зависит от изменения другого – одна из важнейших задач статистики. При этом следует различать функциональные и корреляционные связи. Если каждому значению одной переменной строго соответствует одно определенное значение другой переменной, или, другими словами, обе переменные находятся во взаимно однозначном соответствии, то мы имеем дело с функциональной связью (зависимостью). Если же одному значению переменной (х) вследствие наслоения различных причин может соответствовать множество значений другой переменной (у), то такую связь называют корреляционной.

Примером корреляционной зависимости может служить зависимость производительности труда от стажа работы, зависимость урожайности от сроков сева и т.п.

Наиболее простым случаем корреляционной зависимости является парная корреляция, то есть зависимость между двумя признаками, один из которых называется результативным (у), а другой – факторным (х).

Основными задачами при изучении корреляционных зависимостей являются следующие:

1. Устанавливается наличие корреляции (связи)между величинами у и х. Для этого необходимо лишь визуализировать исходную информацию на графике, где по оси х отображается факторный признак, а по оси у – результативный признак.

2. Устанавливается форма линии связи (регрессии) методом наименьших квадратов (м.н.к.), то есть отыскивается такая математическая формула, которая бы выражала зависимость у от х, при которой сумма квадратов разностей между фактическими наблюдениями (у) зависимой переменной и расчетными значениями переменной по регрессионной формуле (у) МИНИМАЛЬНА, что можно записать следующим образом:

S = S (y_i – ŷ_i)² ® min, (5)

^I⁼¹

где N – число пар эмпирических значений х_i и y_i . В этой связи необходимо сделать специальную оговорку в отношении нижнего индекса у переменной ŷ_i. Поскольку ŷ не дискретная, а котинууальная (непрерывная) зависимость, например, линейного вида

ŷ = а + bx., (6)

то вычисляются значения ŷ для значений x_i , взятых из исходных данных.

Совместное решение по выражениям (5) и (6) является решением задачи аппроксимации, когда эмпирические связи моделируются в виде некоторой (не обязательно линейной) функции. В данном случае уравнение связи (6) и является уравнением регрессии, а если точнее – уравнением линейной регрессии.

После нахождения вида связи х и у необходимо решить еще две следующие задачи.

3. Определяются параметры линии регрессии (здесь – величины и знаки коэффициентов а и b уравнения регрессии (6).

4. Определяются достоверность отдельных параметров (здесь - а и b) и достоверность выбранной нами зависимости (здесь - ŷ = а + bx).

Достоверность отдельных параметров обычно в статистической литературе называется «значимость коэффициентов по Стьюденту», а достоверность выбранной нами зависимости при решении задачи аппроксимации называется «надежностью уравнения по Фишеру». В обоих случаях речь идет о проверке так называемых «нулевых гипотез». В случае полученных величин коэффициентов нулевая гипотеза Н₀ состоит в том, что мы полагаем, что полученные значения коэффициентов не отличаются от нуля с наперед заданной вероятностью (в социально-экономических исследованиях обычно принимают вероятность, равную 90% или 95%). В случае исследования надежности полученного уравнения в целом Н₀ состоит в том, что все коэффициенты не отличаются от нулевых с теми же заданными вероятностями.

В случае опровержения Н₀в обоих случаях уравнение выбранного вида принимается для дальнейшего применения в соответствии с целями исследования (анализ, оценки, прогнозы и др.) в качестве производственной функции.

Обычно на практике, кроме линейной вида (6), используют следующие формы зависимостей:

1) степенная ŷ = ах^b,

2) гиперболическая ŷ = а + — ,

3) показательная ŷ = ab^x,

4) логарифмическая ŷ = a +blgx

5) параболическая ŷ = a +bx + сх²

и ряд других. Как правило, для этих целей используют специальные компьютерные программы, которые последовательно решают задачу аппроксимации для всего набора парных зависимостей. Например, в пакетах прикладных программ (ППП), таких, как широко распространенные Статграфик и SPSS набор парных зависимостей неодинаков. Выбирается для дальнейшего применения такая зависимость, которая отличается от эмпирической зависимости меньшей величиной ошибки аппроксимации – то есть статистического отличия между эмпирическими исходными данными и данными, полученными в результате применения метода наименьших квадратов в отношении выбранного вида зависимости.

Далее рассмотрим процесс получения уравнения линейной регрессии вида (6).

Сущность метода наименьших квадратов

Снова запишем вид соотношения (5) и распишем его подробнее:

_{N N N}

S = S (y_i – ŷ_i)² = S [y_i – (a + bx_i)]² = S (y_i – a - bx_i)²® min. (7)

^{I=1 I=1 I=1}

Далее потупим так, как и в случае с вышеприведенным примером по нахождению экстремума у функции вида (1), с тем лишь отличием, что в качестве неизвестных переменных будем рассматривать не функцию у, а коэффициенты уравнения (5) а и b. С целью упрощения последующих записей переменные у знака суммы и остальные индексы обозначать не будем.

Для решения поставленной задачи продифференцируем выражение (7) по двум неизвестным а и b в так называемых частных производных.

∂S

— = 2 S (y – a - bx) (0 – 1 - 0) = 2 S (y – a - bx) (-1) = 0. (8)

∂a

Разделим обе части равенства (8) на (-1), в правой части равенства (8) останется 0. Понятно, 2 ≠ 0, следовательно,

S (y – a - bx) = 0. (9)

Распишем выражение (9) следующим образом.

S (y – a - bx) = Sу - Sа - Sb = 0; Sу = Sа + b Sх = а S + b Sх.

Поскольку S = S1= (1 + 1 + … + 1) = N, то выражение (9) примет вид:

S у = аN + b Sх (10)

В уравнении (10) все переменные, то есть Sу, Sх и N, – известные величины, суть исходные данные для получения уравнения регрессии, коэффициент а – неизвестная величина.

Проделаем подобные операции по отношению к еще одной неизвестной величине – коэффициенту b.

∂S

— = 2 S (y – a - bx) (0 – 0 – x) = 2 S (y – a - bx) (-x) = 0. (11)

∂b

Если в выражении (11) 2 ≠ 0, то остальная часть равенства (11) примет вид:

S (yx – ax – bx²) = Syx - Sax - S bx²= 0;

Sxy = a Sx + b Sx² (12)

Таким образом, выражение (8) и (12) составляют систему двух уравнений (13) с двумя неизвестными, коэффициентами а и b, а это, в свою очередь, означает, что данная система уравнений – имеет единственное решение.

æ а N + b Sх = Sу

{ (13)

è a Sx + b Sx²= Sxy

Решение системы уравнений (13) может быть осуществлено несколькими способами: методом подстановки, когда одно неизвестное выражается через другое, методом Крамера (метод определителей) и матричным методом. Заметим, однако, что применение первых двух способов оправдано лишь в случаях, когда число неизвестных не превышает трех. Матричный метод – наиболее универсальный, и именно он используется в вычислительных процедурах на ЭВМ средствами ППП, что рассмотрим несколько ниже.

Для решения системы уравнений (13) воспользуемся методом определителей, как наиболее наглядным, для чего перепишем систему (13) в следующем виде.

(для а) (для b) (для правых частей выражения 13)

| N Sх | | Sу |

| | = | | (14)

| Sх Sx²| | Sxy |

Вычислим главный и частные определители по известным правилам, когда столбцы при соответствующих неизвестных замещаются правыми частями выражения (14):

∆ = N Sx² - (Sх )² ,

∆ _a= Sу Sx²- Sх Sxy ,

∆ _b= N Sxy - Sх Sу.

Тогда искомые значения коэффициентов а и b будут следующими:

∆ _a Sу Sx²- Sх Sxy

а = — = ——————— , (15)

∆ N Sx² - (Sх )²

∆ _b N Sxy - Sх Sу

b = — = ——————— , (16)

∆ N Sx² - (Sх )²

Если коэффициенты регрессии а и b вычислены правильно, то в этом легко убедиться по тождеству (16а), иллюстрирующего тот факт, что если мы подставим среднее значение х, то при найденных коэффициентах получим среднее значение у:

у_ср ≡ а + b х_ср . (16а)

Далее рассмотрим процесс нахождения величин коэффициентов линейной функции вида (6) на конкретном, т.н. «модельном» примере.

Пример. В качестве примера обратимся к следующим исходным данным. Пусть некая фирма в текущем году с января по июнь располагает следующими данными по ежемесячной прибыли: в январе, феврале и марте – по 1 тыс.руб.; в апреле – 3 тыс.руб.; в мае – 4 тыс.руб. Требуется построить прогноз ожидаемой прибыли на июнь и оценить ее достоверность – при прочих равных условиях. Под равными условиями этим имеется в виду неизменность (постоянство) внутренних и внешних условий деятельности фирмы (структура производства, позиционирование продукции, коньюнктура, уровень инфляции и др.).

Введем обозначения. Поскольку мы имеем дело с моментным временным рядом, представим месяцы как варианты вариационного ряда – элементы множества Х = {x_i}, где x_i – месяцы текущего года, i=1,n; n=5. То есть x₁= 1 (первый месяц), x₂= 2, x₃= 3, x₄= 4, x₅= 5 (пятый месяц). Тогда прибыль У = {y_i}, где y_i - ежемесячная прибыль в тыс.руб.

Исходные (эмпирические) данные в принятых нами обозначениях представим в виде рабочей таблицы (табл. 2). Причем в табл. 2 предусмотрим такие столбцы, наличие которых позволило бы вычислить все элементы формул (15) и (16).

Таблица 2

Эмпирические данные и промежуточные вычисления

i	x_i	y_i	x_i y_i	x_i²	y_i²
1 2 3 4 5	1 2 3 4 5	1 1 1 3 4	1 2 3 12 20	1 4 9 16 25	1 1 1 9 16
Si = N = 5	Sx_i = 15	Sy_i = 10	Sx_i y_i = 38	Sx_i²= 55	Sy_i²= 28

Опуская для большей наглядности индексы и подставляя данные табл. 2 в выражения (15) и (16), получим следующее.

Sу Sx²- Sх Sxy 10•55 - 15•38 550 – 570 - 20

а = ——————— = —————— = ———— = —— = - 0,4; (17)

N Sx² - (Sх )² 5•55 - (15)²275 - 225 50

N Sxy - Sх Sу 5•38 - 15•10 190 – 150 40

b = ——————— = —————— = ———— = —— = + 0,8. (18)

N Sx² - (Sх )²5•55 - (15)²275 - 225 50

Коэффициенты найдены, и символьное выражение (6) примет явный вид:

ŷ = - 0,4 + 0,8 • х.. (19)

Осуществим проверку корректности вычисления коэффициентов уравнения линейной регрессии по выражению (16а). Тождество (16а) выполняется:

2 ≡ - 0,4 + 0,8 • 3 = - 0,4 + 2,4 = 2

Следовательно, коэффициенты а и b найдены верно.

Выражение (19) относится ко всем действительным значениям х. Однако для нас представляет интерес именно его вещественные значения - дискретные положительные значения – 1, 2, 3 и т.д., - в частности нас интересует прибыль в 6-м месяце текущего года (в июне). Поэтому перепишем (19) с учетом ранее опущенных индексов:

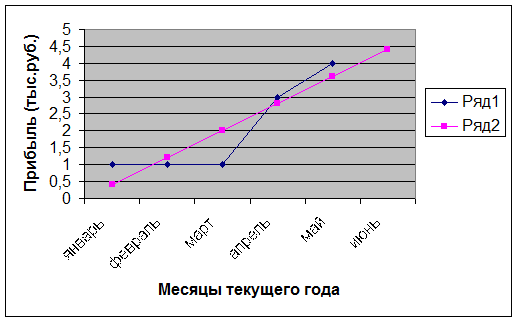
Рис. 2. Эмпирические данные, линия регрессии и прогноз.

ŷ_i = - 0,4 + 0,8х_i. (20)

Для нахождения прогнозного значения прибыли достаточно в выражение (20) подставить х₆=6:

ŷ_i = - 0,4 + 0,8х_i = - 0,4 + 0,8•6 = -0,4 + 4,8 = 4,4 (тыс.руб.). (21)

Эмпирические данные (Ряд 1), линия регрессии и прогноз на следующий месяц (Ряд 2) приведены на рис. 1.

Вполне очевидно, что в общем случае прогноз тем точнее, чем период ретроспекции (здесь - январь-май, то есть 5 месяцев) больше прогнозируемого периода (здесь - июнь, то есть 1 месяц). Иными словами, картину, полученную в виде (19) или (20), мы экстраполируем за пределы проведенной нами аппроксимации – представления некоторой эмпирической зависимости (2 и 3 столбцы табл. 1) в виде некоторой аналитической функции (19), в данном случае – линейной.

Заметим также, что с января по май в одноименных точках по оси абцисс ОХ сумма квадратов разностей эмпирических значений прибыли У (Ряд 1) и их аналитических значений по выражению (20) (Ряд 2) будет минимальной в рамках любой другой линейной функции, то есть функции со значениями коэффициентов а и b, отличных от найденных (а≠-0,4; b≠0,8), что и составляет сущность метода наименьших квадратов (МНК), символически записанной в выражении (5).

Y Y

y = a + bx y = a - bx

0 X 0 X

Рис. 3 Рис. 4

Y Y

y = -a + bx y = a

0 X 0 X

Рис. 5 Рис. 6

Во всех приведенных случаях значение коэффициент «а» со своим знаком иллюстрируется величиной ординаты, отсекаемой прямой от оси ОY. Значение коэффициента «b» есть не что иное, как величина тангенса угла наклона прямой к оси ОХ (отношение длины катета, противолежащего углу, к длине катета, прилежащего к углу). Особенно это наглядно можно проиллюстрировать на примере уравнения прямой y = а + bx, если а = 0, а b = 1, то есть y = 0 + 1x = х.

Иными словами, уравнение у = х является уравнением биссектрисы угла, которое делит координатную плоскость строго пополам; тангенс такого угла равен единице: какое значение задаем на оси ОХ, такое же значение получим и по оси OY. И если свободный член уравнения прямой отражает пересечение оси OY в точке 0 на оси OX, то коэффициент при аргументе «х» отражает скорость изменения функции «у».

Действительно, если при увеличении х величина у возрастает (рис. 3, 5), то значение b > 0, скорость изменения у положительна. И наоборот: если при увеличении х величина у убывает (рис. 2), то значение b < 0, скорость изменения у отрицательна. Если же при увеличении х величина у остается без изменений (рис. 6), то значение b = 0, скорость изменения у равна нулю или отсутствует: y = const.

Итак, после того, как искомые коэффициенты уравнения линейной регрессии а и b найдены и прогноз построен, для завершения поставленной задачи остается оценить точность аппроксимации, вычислить величину коэффициента линейной корреляции, а также оценить значимость полученных коэффициентов и надежность уравнения в целом.

Дата добавления: 2021-01-20; просмотров: 51; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!