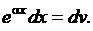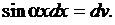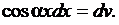Интегрирование методом подведения
Под знак дифференциала
Метод интегрирования «подведением под знак дифференциала» основан на свойстве инвариантности интеграла.
Таблицу интегралов можно переписать следующим образом:
Таблица 2
1. 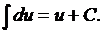
2. 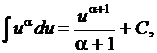

3. 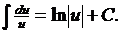
4. 
5. 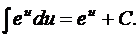
6. 
7. 
8. 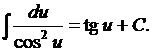
9. 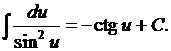
10. 
11. 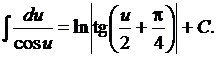
12. 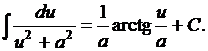
13. 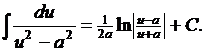
14. 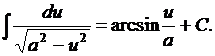
15. 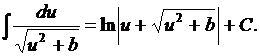
Основная формула, которую мы используем в этом параграфе, следующая:
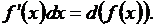
Запишем таблицу подведения под знак дифференциала. Она похожа и на таблицу производных (дифференциалов) и на таблицу интегралов. Помним, что операция подведения под знак дифференциала есть операция интегрирования, так как под дифференциалом оказывается первообразная для функции, находящейся в левой части формулы перед dx .
Таблица 3
1. 
2. 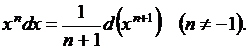
3. 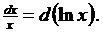
4. 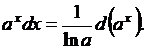
5. 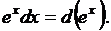
6. 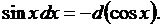
7. 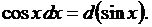
8. 
9. 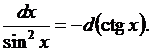
10. 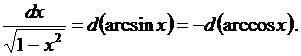
11. 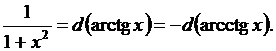
Примеры применения формулы 1 были разобраны в §2. Обратимся к другим формулам.
1. Найти 
Применим формулу 5 из таблицы 3: 
Тогда 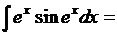
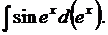
Используя свойство инвариантности где 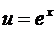 и табличный интеграл
и табличный интеграл  получим
получим
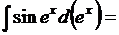

Легко проверить дифференцированием, что интеграл найден верно:
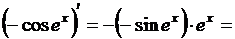
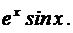
2. Найти 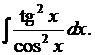
Решение.
Применим формулу 8 таблицы 3 и табличный интеграл 2 таблицы 2:

3. Найти 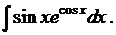
Решение.
Воспользуемся формулой 6 из таблицы 3.
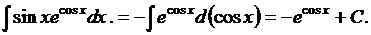
4. Найти 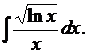
Решение.
Воспользуемся формулой 3 из таблицы 3 и табличным интегралом 3 из таблицы 2.
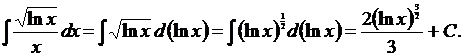
5. Найти 
Здесь нам придется применить подведение под дифференциал дважды. Сначала воспользуемся формулой 1 таблицы 3: 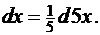

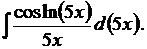
Теперь воспользуемся формулой 3 таблицы 3 и табличным интегралом 7 таблицы 2:

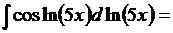

6. Найти 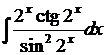 .
.
Решение.
Сначала воспользуемся формулой 4 из таблицы 3, а затем формулой 9 таблицы 3 и табличным интегралом 2 таблицы 2:
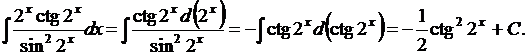
7. Найти 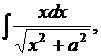 где a – любое число.
где a – любое число.
Решение.
Под дифференциалом нужно получить выражение 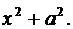 Для этого используем формулы 1 и 2 из таблицы 3 и 2а таблицы 2.
Для этого используем формулы 1 и 2 из таблицы 3 и 2а таблицы 2.
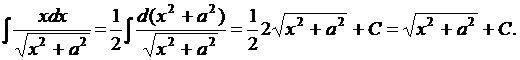
Примеры для самостоятельного решения
| Задание. | Ответ. |
1. 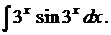
| 
|
2. 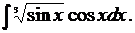
| 
|
3. 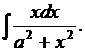
| 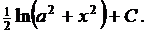 (Рекомендуется внести в таблицу) (Рекомендуется внести в таблицу)
|
4. 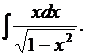
|  (Рекомендуется внести в таблицу) (Рекомендуется внести в таблицу)
|
5. 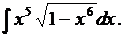
| 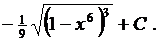
|
6. 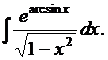
| 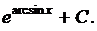
|
7. 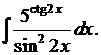
| 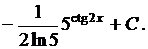
|
Интегрирование по частям
Формула интегрирования по частям
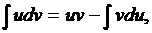
где u, v – дифференцируемые функции.
Применение формулы целесообразно, если интеграл 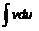 проще исходного интеграла или подобен ему.
проще исходного интеграла или подобен ему.
В качестве u выбирается функция, которая упрощается в результате дифференцирования, а в качестве 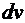 – оставшаяся часть подынтегрального выражения, из которой интегрированием можно найти
– оставшаяся часть подынтегрального выражения, из которой интегрированием можно найти 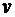 . При этом
. При этом 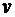 – одна из первообразных, и, определяя
– одна из первообразных, и, определяя 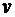 , произвольную постоянную учитывать не будем.
, произвольную постоянную учитывать не будем.
Для некоторых интегралов можно дать общие рекомендации при интегрировании по частям. Эти рекомендации представим в виде таблиц.
Таблица 4
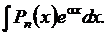
| 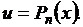
|
| |
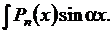
| 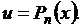
|
| |

| 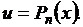
|
| |
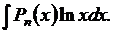
| 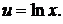
| 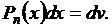
| |
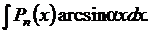
| 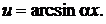
| 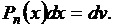
| |
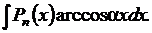
| 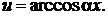
| 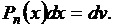
| |

| 
| 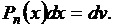
| |

| 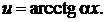
| 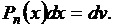
| |
 – многочлен от x степени n.
– многочлен от x степени n.
Примеры.
1 Найти 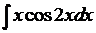 .
.
Решение.
Пользуясь рекомендацией таблицы 4, выберем
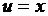 ,
, 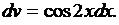 Далее следует найти du и v.
Далее следует найти du и v.

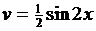 , так как
, так как 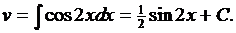
Заметим, что при нахождении 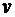 указывается одна из первообразных (произвольная постоянная не нужна). Используя формулу интегрирования по частям, получаем
указывается одна из первообразных (произвольная постоянная не нужна). Используя формулу интегрирования по частям, получаем
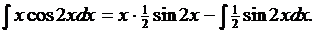
Итак, мы получили более простой интеграл  Найдя его и добавив постоянную C, получаем все семейство первообразных и окончательный ответ:
Найдя его и добавив постоянную C, получаем все семейство первообразных и окончательный ответ:
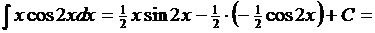
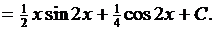
В дальнейшем для удобства и наглядности будем оформлять запись подстановок определенным образом. Рассмотренный пример выглядит так:
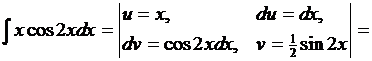
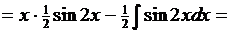

1. Найти 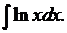
Решение.
Пользуясь таблицей 4, выберем 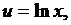
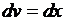 . Получим
. Получим
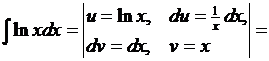
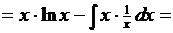

3. Найти 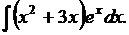
Решение.
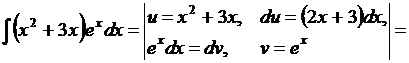
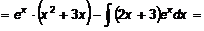
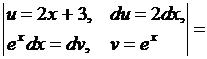

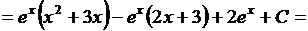
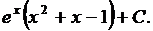
Обратите внимание на то, что в этом примере интегрирование по частям применено дважды. Причем, на первом этапе было видно, что мы на правильном пути, так как, понизив степень многочлена, мы уже упростили интеграл.
3. Найти 
Решение.
Для этого интеграла нет рекомендаций в таблице 4.
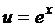 ,
, 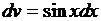 ,
, 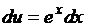 ,
, 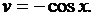
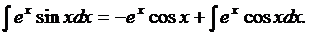
Мы не получили интеграл проще, а получили подобный. Применим формулу интегрирования по частям еще раз:

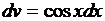 ,
, 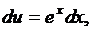
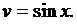

В правой части мы получили исходный интеграл. Перенесем его в левую часть:
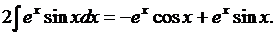
Следовательно,

Осталось добавить произвольную постоянную. Окончательно имеем
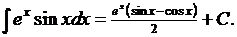
Интегралы такого типа называются «возвратными», так как в процессе преобразований мы возвращаемся к исходному интегралу.
4. Найти 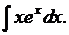
Решение.
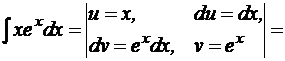
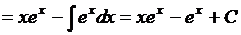 .
.
5. Найти 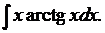
Решение.
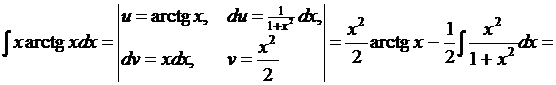
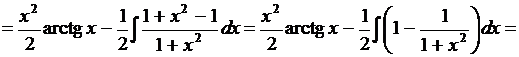

Примеры для самостоятельного решения.
| Задание | Ответ |
1. 
| 
|
2. 
| 
|
3. 
| 
|
4. 
| 
|
Дата добавления: 2021-01-20; просмотров: 66; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!