Контрольные задачи (1 семестр)
Практика 9. (8 дек 932025, 10 дек 932024)
Задача 50. Найти 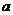 , при котором ранг равен 2.
, при котором ранг равен 2.
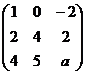
Решение. Преобразуем:
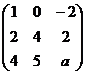



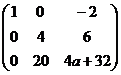

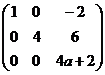
Последняя строка состоит из нулей при 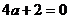 , т.е.
, т.е. 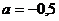 .
.
Ответ. 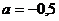 .
.
Задача 5 1. Найти 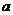 , при котором ранг равен 2.
, при котором ранг равен 2.

Решение.

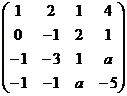

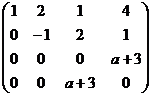 Ответ.
Ответ.  .
.
Глава 3.
Системы линейных алгебраических уравнений.
Задача 1. Решить систему линейных уравнений 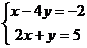 .
.
Решение. А. Матричным методом.
Запишем систему в виде: 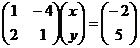 .
.
Найдём обратную матрицу для А.
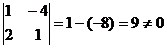 .
.

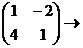
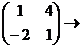
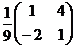
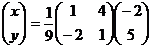 =
= 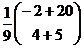 =
= 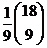 =
=  .
.
Б. Методом Крамера.
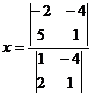 =
= 
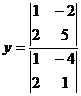 =
= 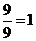 .
.
Ответ.  .
.
Метод Гаусса.
Задача 2. Решить систему уравнений 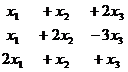

Решение. Построим расширенную матрицу и преобразуем её.

чтобы обнулились коэффициенты ниже левого верхнего угла, то есть чтобы исчезла переменная 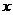 из всех уравнений кроме первого, надо:
из всех уравнений кроме первого, надо:
а) из 2-й строки вычесть 1-ю;
б) из 3-й строки вычесть удвоенную 1-ю.
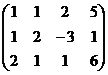

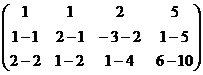 =
= 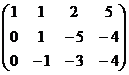
Теперь, чтобы обнулить ниже чем 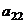 , нужно к 3-й строке просто прибавить 2-ю, так как знаки там противоположны. При этом структуру из нулей, которые уже получились слева, мы на последующем шаге всё равно никак не испортим, ведь там к 0 будет прибавляться 0 либо вычитаться 0, то есть ступенчатая структура там уже всё равно будет сохраняться.
, нужно к 3-й строке просто прибавить 2-ю, так как знаки там противоположны. При этом структуру из нулей, которые уже получились слева, мы на последующем шаге всё равно никак не испортим, ведь там к 0 будет прибавляться 0 либо вычитаться 0, то есть ступенчатая структура там уже всё равно будет сохраняться.
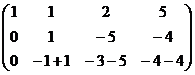 =
= 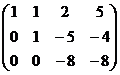
Когда в основной матрице уже получена треугольная структура, снова перепишем в виде системы
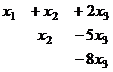
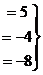 В первом уравнении 3 неизвестных, а в каждом следующем всё меньше и меньше, а в последнем вообще только одна неизвестная. Именно этой цели мы и хотели добиться, приводя к треугольному виду: из последнего уравнения можно теперь сразу выразить
В первом уравнении 3 неизвестных, а в каждом следующем всё меньше и меньше, а в последнем вообще только одна неизвестная. Именно этой цели мы и хотели добиться, приводя к треугольному виду: из последнего уравнения можно теперь сразу выразить 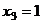 . Затем с этой информацией мы поднимаемся в предпоследнее уравнение, где две неизвестных, впрочем, одна из них уже известна.
. Затем с этой информацией мы поднимаемся в предпоследнее уравнение, где две неизвестных, впрочем, одна из них уже известна.
|
|
|
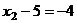
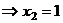 .
.
А теперь уже две последних неизвестных стали известны, и с этой информацией поднимаемся в 1-е уравнение, подставляя туда 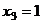 и
и 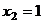 . Итак,
. Итак, 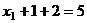
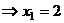 .
.
Ответ. 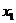 =2,
=2, 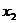 =1,
=1, 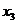 =1.
=1.
Можно ответ записать и в виде вектора: 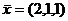 .
.
Ответ. 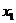 =2,
=2, 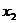 =1,
=1, 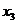 =1.
=1.
Задача 3. Решить систему уравнений 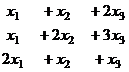

(как в прошлой, но у элемента 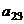 изменили знак).
изменили знак).
Решение. Построим расширенную матрицу и преобразуем её.
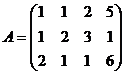
чтобы обнулились коэффициенты ниже левого верхнего угла, то есть чтобы исчезла переменная  из всех уравнений кроме первого, надо:
из всех уравнений кроме первого, надо:
а) из 2-й строки вычесть 1-ю;
б) из 3-й строки вычесть удвоенную 1-ю.
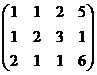

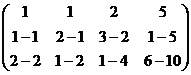 =
= 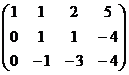
Теперь, чтобы обнулить ниже чем 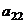 , нужно к 3-й строке просто прибавить 2-ю, так как знаки там противоположны. При этом структуру из нулей, которые уже получились слева, мы на последующем шаге всё равно никак не испортим, ведь там к 0 будет прибавляться 0 либо вычитаться 0, то есть ступенчатая структура там уже всё равно будет сохраняться.
, нужно к 3-й строке просто прибавить 2-ю, так как знаки там противоположны. При этом структуру из нулей, которые уже получились слева, мы на последующем шаге всё равно никак не испортим, ведь там к 0 будет прибавляться 0 либо вычитаться 0, то есть ступенчатая структура там уже всё равно будет сохраняться.
|
|
|
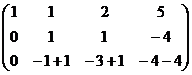 =
= 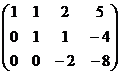
Когда в основной матрице уже получена треугольная структура, снова перепишем в виде системы
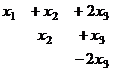
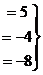 В первом уравнении 3 неизвестных, а в каждом следующем всё меньше и меньше, а в последнем вообще только одна неизвестная. Именно этой цели мы и хотели добиться, приводя к треугольному виду: из последнего уравнения можно теперь сразу выразить
В первом уравнении 3 неизвестных, а в каждом следующем всё меньше и меньше, а в последнем вообще только одна неизвестная. Именно этой цели мы и хотели добиться, приводя к треугольному виду: из последнего уравнения можно теперь сразу выразить 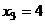 . Затем с этой информацией мы поднимаемся в предпоследнее уравнение, где две неизвестных, впрочем, одна из них уже известна.
. Затем с этой информацией мы поднимаемся в предпоследнее уравнение, где две неизвестных, впрочем, одна из них уже известна.
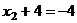
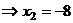 .
.
А теперь уже две последних неизвестных стали известны, и с этой информацией поднимаемся в 1-е уравнение, 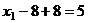
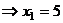 .
.
Ответ. 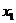 =5,
=5, 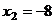 ,
, 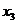 =4.
=4.
Можно ответ записать и в виде вектора: 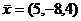 .
.
Задача 4. Решить систему уравнений 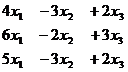
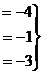
Решение. При построении расширенной матрицы, сразу же домножим 2-е и 3-е уравнения на такие коэффициенты, чтобы в начале строки были числа, кратные угловому элементу. А именно, 2-ю строку на 2, а 3-ю строку на 4. Так надо, чтобы потом в методе Гаусса можно было не домножать на дробные коэффициенты при вычитании строк.
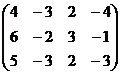



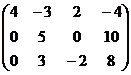

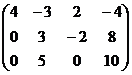
Чем ниже, тем меньше переменных. Идея метода Гаусса соблюдена.
Сначала можно найти х2, затем х3, позже х1.
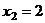 , тогда
, тогда 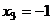 . Тогда
. Тогда  .
.
Замечание. Впрочем, в данном случае можно заметить, что совпадает существенная часть 1 и 3 строк, и если сразу вычесть 1-ю строку из 3-й, то можно будет тут же найти 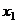 .
.
|
|
|
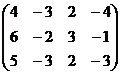

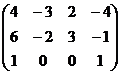
Из 3-го уравнения теперь следует  .
.
А далее можно составить более простую систему на  , уже с учётом
, уже с учётом  .
.
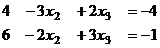
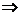
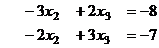
Теперь домножим, чтобы получить кратное, и приведём к треугольной структуре.
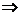
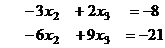
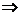
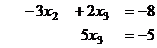
Из последнего 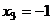 , а далее
, а далее 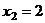 .
.
Ответ.  ,
, 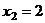 ,
, 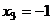 .
.
- - - Перерыв - - -
Задача 5. Решить систему уравнений 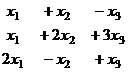
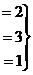
Решение. Составим расширенную матрицу.
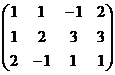

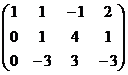

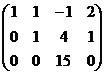
Получили эквивалентную систему:
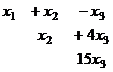
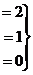 , из последнего уравнения, очевидно,
, из последнего уравнения, очевидно, 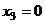 ,
,
тогда из предпоследнего 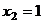 , и из 1-го
, и из 1-го  .
.
Ответ.  .
.
Задача 6. Решить систему уравнений 
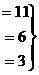
Решение. Во-первых, можно всё 2-е уравнение сократить на 2, так удобнее для решения, числа будут меньше. Затем обнуляем ниже углового элемента: вычитаем из 2-го уравнения удвоенное 1-е, а также 3-го 1-е.
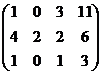

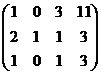

 =
=
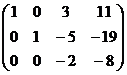 треугольная структура уже получилась.
треугольная структура уже получилась.
Перепишем снова в виде системы:
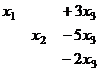
 из 3-го уравнения
из 3-го уравнения 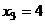 , подставляем во 2-е, там получается
, подставляем во 2-е, там получается 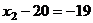
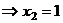 .
.
А из 1-го 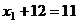
 .
.
Ответ. 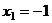 ,
, 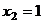 ,
, 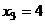 .
.
Задача 7. Решить систему уравнений 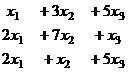
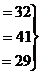
Решение.
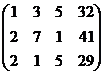

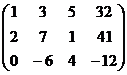

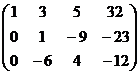

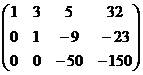


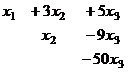
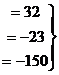
Из последнего, 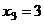 . Тогда из 2-го
. Тогда из 2-го 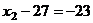 ,
, 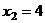 .
.
Тогда из 1-го  ,
,  .
.
Ответ. (5,4,3).
|
|
|
Задача 8. Решить систему уравнений
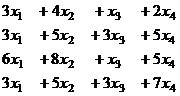
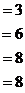
Решение.
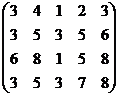

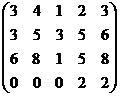

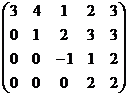
Система приведена к виду:
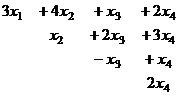
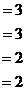
Из последнего,  , тогда
, тогда 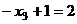
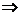
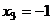 .
.
Тогда из 2-го:  ,
, 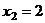 .
.
И наконец из 1-го, 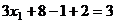
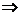
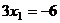
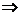
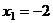 .
.
Ответ. 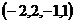 .
.
Задача 9. Решить систему уравнений
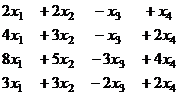
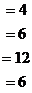
Решение. Здесь удобнее метод Гаусса начать с 4 столбца (зеркально), так как там коэффициенты, кратные 1.


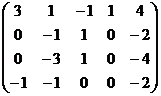

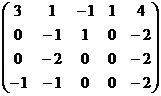
Из двух последних: 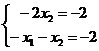
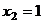 ,
,  .
.
Тогда из первых двух уравнений:

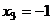 ,
, 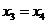 .
.
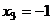 ,
,  .
.
Ответ. 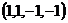 .
.
Практика 10. (9 дек 932025, 12 дек 932024)
Задача 10. Решить систему уравнений.

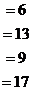
Решение.


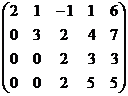

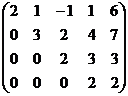
Разворачиваем обратно в систему:
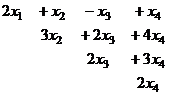
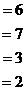
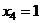
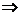


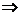
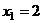 .
.
Ответ. 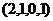 .
.
Неопределённые системы (  ).
).
Задача 11. Решить неоднородную систему 
Решение. 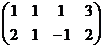

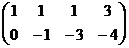

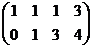 .
.
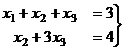

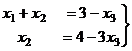 .
.
Из 1-го: 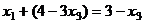 ,
, 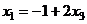
Ответ. Общее решение 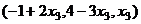 .
.
Частные решения:  ,
,  , ...
, ...
Для сравнения, методом Крамера.
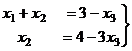
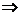
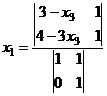 =
= 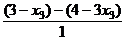 =
= 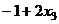 .
.
 =
= 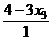 =
=  .
.
То же самое.
Задача 11-Б. Решить однородную систему 
Решение. 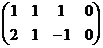

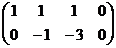

 .
.


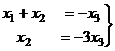 .
.
Из 1-го: 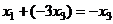 ,
, 
ФСР 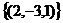 . Обратите внимание, что это и есть разность двух частных решений прошлой задачи.
. Обратите внимание, что это и есть разность двух частных решений прошлой задачи.
Ответ. Общее решение  . ФСР
. ФСР 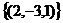 .
.
Задача 12. Решить неоднородную систему.

Решение. Построим и преобразуем расширенную матрицу.
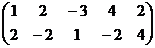

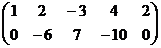
Базисный минор в первых двух столбцах, последние две переменные свободные, переносим их вправо.
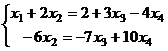
Отсюда 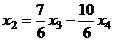 . Тогда
. Тогда 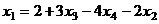 =
=
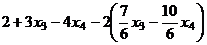 =
=  =
=
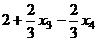 .
.
Ответ. Общее решение: 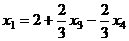 ,
, 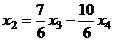 .
.
Частное например (2,0,0,0).
Задача 13. Решить неоднородную систему 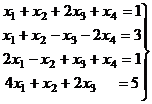
Решение. Запишем расширенную матрицу системы.
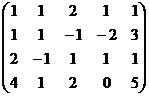
обнулим всё ниже углового элемента, для этого:
из 2-й строки вычтем 1-ю, из 3-й удвоенную 1-ю, из 4-й 1-ю, домноженную на 4.
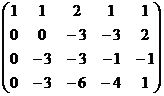
теперь можно поменять местами 2 и 3 строки, а также домножить на  три последних уравнения (там почти везде были знаки минус)
три последних уравнения (там почти везде были знаки минус)
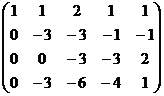

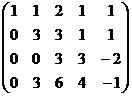
затем из 4-й строки вычитаем 2-ю, чтобы продолжить стандартную процедуру метода Гаусса, потом видим что 3-я и 4-я стали одинаковы, тогда из 4-й вычитаем 3-ю. Получается, что 4-е уравнение 0 = 0.



Итак, осталось 3 уравнения, базисный минор легко заметить в первых трёх столбцах (там треугольная структура матрицы, и этот определитель явно отличен от 0). 4-й столбец не входит в базисный минор, то есть 4-я переменная свободная, т.е. когда будем записывать систему, переносим её через знак равенства во всех уравнениях.
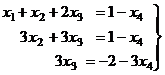
Из последнего уравнения 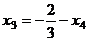 , подставляя это выражение во 2-е уравнение, выразим
, подставляя это выражение во 2-е уравнение, выразим  .
. 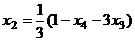 =
= 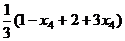 ,
,
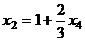 . Далее из 1-го уравнения:
. Далее из 1-го уравнения:
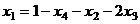 =
=  ,
,
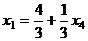 . Итак, общее решение:
. Итак, общее решение:
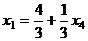 ,
, 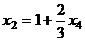 ,
, 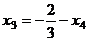 .
.
Можно записать в виде вектора:  .
.
Если задать, например,  получим частное решение:
получим частное решение: 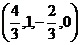 .
.
Ответ. Общее решение:  .
.
Задача 14. Решить неоднородную систему 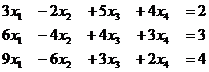
Решение.
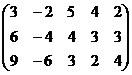

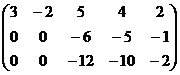

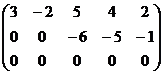
Вычёркивается лишнее 3-е уравнение.
Базисный минор не может быть в 1 и 2 столбце. Или 1 и 3, или 1 и 4. Лучше 1 и 4, чтобы делить на 5.

Получили систему:
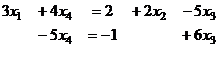
Из второго: 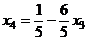 подставляем в 1-е:
подставляем в 1-е:
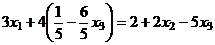
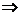
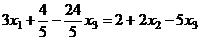
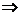
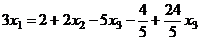
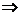
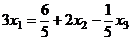
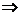
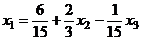 .
.
Общее решение: 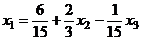 ,
, 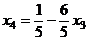
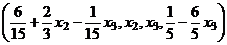 .
.
Частное решение: 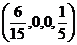 . Подставим во все 3 уравнения, проверим.
. Подставим во все 3 уравнения, проверим.
- - - Перерыв - - -
Задача 15.
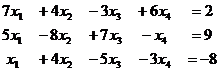
Решение.
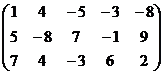

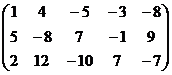

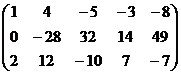

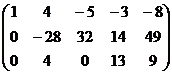

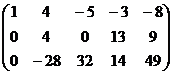

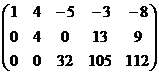
Получили систему:
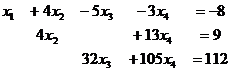
 свободная переменная, базисный минор в 1,2,3 столбцах.
свободная переменная, базисный минор в 1,2,3 столбцах.
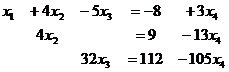
Из последнего:  из второго:
из второго:  .
.
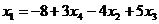 =
= 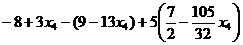 =
=
 .
.
Общее решение:
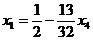 ,
,  ,
,  .
.
Частное решение (2/4, 9/4, 14/4, 0)
Практика 11 (15 дек 932025, 17 дек 932024)
Однородные системы.
Задача 16. Решить однородную систему 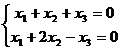 .
.
Решение. Можно записать основную матрицу и там вычесть 1-ю строку из 2-й, впрочем, можно для небольшой системы сделать это и сразу в системе, вычесть 1-е уравнение из 2-го. Получится:
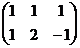

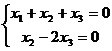
Ранг равен 2, а неизвестных 3, 3-я неизвестная свободная, переносим вправо. Тогда: 
Из 2-го уравнения 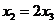 , тогда
, тогда 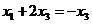 , а значит
, а значит 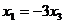 .
.
Общее решение: 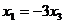 ,
, 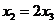 . В виде вектора:
. В виде вектора:  .
.
Присвоим  , получим остальные неизвестные.
, получим остальные неизвестные.
ФСР состоит всего из одного вектора: 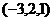 . Все остальные решения пропорциональны этому.
. Все остальные решения пропорциональны этому.
Если бы, например, присвоили 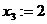 , получили бы
, получили бы 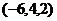 . Это потому, что всего одна свободная переменная.
. Это потому, что всего одна свободная переменная.
Ответ. Общее решение:  , ФСР
, ФСР 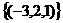 .
.
Задача 17. Решить систему 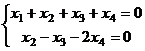
Решение. Минор, состоящий из 1 и 2 столбцов, уже в ступенчатой форме.
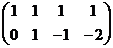
Базисный минор порядка 2. Тогда 3-я и 4-я переменная - свободные. Перенесём их через знак равенства. 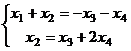 .
.
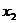 уже фактически выражено:
уже фактически выражено:  , подставим это в первое уравнение, чтобы выразить
, подставим это в первое уравнение, чтобы выразить  .
.
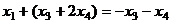
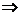
 .
.
Общее решение: {  ,
,  }.
}.
Если поочерёдно присвоить значение 1 каждой из свободных переменных (а другая в это время 0) то получим гарантированно 2 линейно-независимых вектора, они не пропорциональны, так как 1 на разных местах.
 , получим
, получим 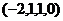
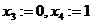 , получим
, получим  .
.
Эти 2 вектора { 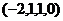 ,
,  } и есть ФСР. Это
} и есть ФСР. Это  частных решений, из которых можно составить любые другие частные решения: любые их линейные комбинации будут частными решениями однородной системы.
частных решений, из которых можно составить любые другие частные решения: любые их линейные комбинации будут частными решениями однородной системы.
Ответ. Общее решение {  ,
,  }.
}.
ФСР { 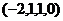 ,
,  }.
}.
Замечание. Для системы с квадратной матрицей справа были только числа, для системы с прямоугольной матрицей к ним добавляются свободные переменные, и там будут выражения типа  . А для однородной системы справа констант нет (они = 0), но туда перенесены свободные переменные. То есть идея решения методом Гаусса во всех этих 3 параграфах одна и та же, но справа разные типы объектов.
. А для однородной системы справа констант нет (они = 0), но туда перенесены свободные переменные. То есть идея решения методом Гаусса во всех этих 3 параграфах одна и та же, но справа разные типы объектов.
Задача 18. Решить однородную систему 
Решение. Запишем основную матрицу, преобразуем её. 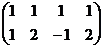

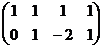
снова представим в виде системы: 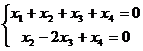
базисный минор порядка 2, можно обвести в левом углу, поэтому 3-я и 4-я переменная - свободные. Здесь их уже две, так как 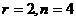 , поэтому
, поэтому  . Перенесём их через знак равенства.
. Перенесём их через знак равенства.
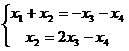
здесь 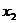 уже выражено:
уже выражено:  , подставим это в первое уравнение, чтобы выразить и
, подставим это в первое уравнение, чтобы выразить и  .
.
 ,
, 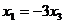 .
.
Общее решение: 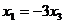 ,
,  .
.
В виде вектора: 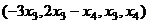 .
.
Если поочерёдно присвоить значение 1 каждой из свободных переменных (а другая в это время 0) то получим гарантированно 2 линейно-независимых вектора, они не пропорциональны, так как число 1 в них на разных местах.
 , получим
, получим 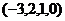
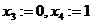 , получим
, получим 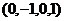 .
.
Эти 2 вектора { 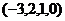 ,
, 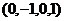 } и есть ФСР. Это
} и есть ФСР. Это  частных решений, из которых можно составить любые другие частные решения. Любые их линейные комбинации будут частными решениями однородной системы.
частных решений, из которых можно составить любые другие частные решения. Любые их линейные комбинации будут частными решениями однородной системы.
Ответ. Общее решение: 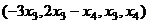 .
.
ФСР это множество из 2 векторов: { 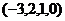 ,
, 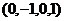 }.
}.
Задача 19. Решить однородную систему, найти ФСР. 
Решение. Запишем основную матрицу системы и преобразуем её методом Гаусса.
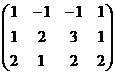

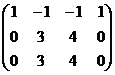

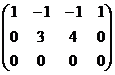
Ранг матрицы равен 2, базисные столбцы 1-й и 2-й. Несмотря на то, что сначала могло показаться, что здесь будет одна свободная переменная (4 переменных и 3 уравнения), на самом деле здесь будет две свободных переменных, ведь 3-е уравнение оказалось линейной комбинацией первых двух. 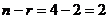 .
.
Снова возвращаемся от матрицы к системе уравнений. 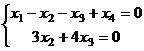
перенесём свободные неизвестные вправо:
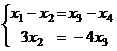 из 2 уравнения
из 2 уравнения  , подставим это в 1-е,
, подставим это в 1-е,
будет 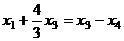 , то есть
, то есть 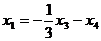 .
.
Общее решение: 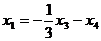 ,
,  .
.
В виде вектора: 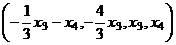
Построим ФСР из 2 векторов.
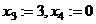 , получим
, получим 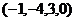
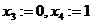 , получим
, получим 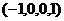 .
.
Так как здесь есть дроби, то для того, чтобы векторы в ФСР содержали только целые координаты, можно задавать не только 1, но и другое число, главное только чтобы в 3 и 4 координатах помещался невырожденный минор. Если мы задаём поочерёдно каждой свободной переменной какое-то число (не обязательно 1) а остальным 0, то линейная независимость этой системы векторов всё равно заведомо обеспечена.
Ответ. Общее решение: 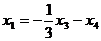 ,
,  .
.
ФСР из 2 векторов: 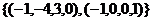 .
.
Задача 20. Решить однородную систему, найти ФСР.
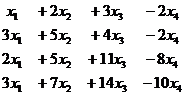
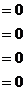
Основная матрица:
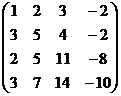
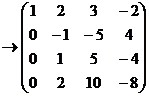

Ранг = 2. n-r = 4-2 = 2 свободных переменных.

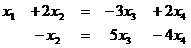
Из 2-го: 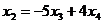 ,
,
тогда из 1-го  ,
, 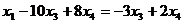
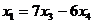
Общее решение: 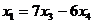 ,
, 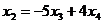 .
.
ФСР 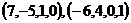 .
.
Задача 21. Решить однородную систему
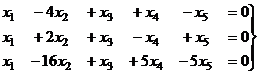
Решение. 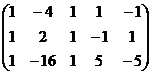

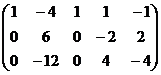

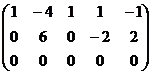 Ранг основной матрицы равен 2. Оставить слева 2 переменных, например,
Ранг основной матрицы равен 2. Оставить слева 2 переменных, например,  , остальные свободные.
, остальные свободные.
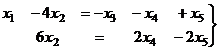
Из второго: 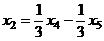 , подставим в 1-е.
, подставим в 1-е.
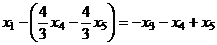 .
.
Тогда  =
=  .
.
Общее решение:  ,
, 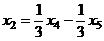
или в векторном виде: 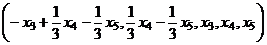 .
.
ФСР: 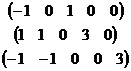
Ответ.
Общее решение: 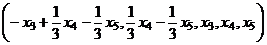 .
.
ФСР: 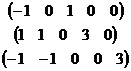
- - - Перерыв - - -
Задача 22. Решить однородную систему, найти ФСР.
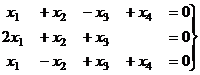
Решение. Преобразуем методом Гаусса основную матрицу системы.
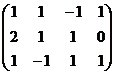

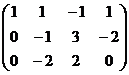

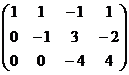
Ступенчатая структура продолжилась до самой последней строки, и не проявилась строка из нулей, то есть ранг равен 3. Здесь всего одна свободная переменная. Развернём обратно эту матрицу, т.е. запишем в виде системы, а затем перенесём свободные переменные вправо.
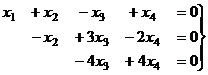

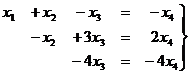
Из последнего,  , это подставим во 2-е и получим
, это подставим во 2-е и получим 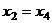 .
.
Затем это всё в 1-е уравнение, получим 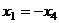 .
.
Общее решение: 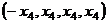 .
.
ФСР: один вектор 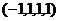 .
.
Ответ. Общее решение: 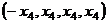 . ФСР:
. ФСР: 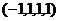 .
.
Задача 23. Решить однородную систему, найти ФСР.

Решение. Преобразуем методом Гаусса основную матрицу системы.
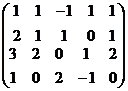

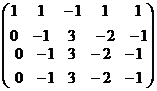 далее можно вычесть 2 строку из 3-й и 4-й, и там везде будут 0.
далее можно вычесть 2 строку из 3-й и 4-й, и там везде будут 0.
Здесь ранг 2, неизвестных 5, 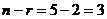 .
.
Переписывая в виде системы, переносим вправо 3 свободных переменных.

Выражаем из 2-го  как линейную функцию от
как линейную функцию от 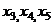 , а затем с помощью 1-го уравнения, также и
, а затем с помощью 1-го уравнения, также и 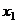 .
.
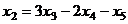 ,
,
подставим в 1-е: 
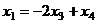 .
.
Общее решение: 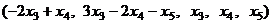 .
.
ФСР из 3 векторов. Для этого задаём поочерёдно 1 какой-либо из свободных переменных, а 0 остальным.
ФСР: 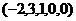 ,
, 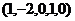 ,
, 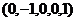 .
.
Ответ. Общее решение: 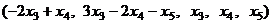 .
.
ФСР: 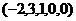 ,
, 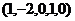 ,
, 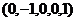 .
.
Задача 24. Решить однородную систему, найти ФСР:
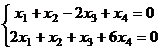
Решение. Сначала быстро преобразуем основную матрицу методом Гаусса, для чего из 2 строки вычтем удвоенную 1-ю.


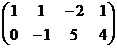 , видим, что базисный минор в 1 и 2 столбцах, тогда
, видим, что базисный минор в 1 и 2 столбцах, тогда 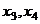 свободные переменные.
свободные переменные.
Система после преобразования: 
Переносим вправо 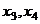 :
: 
Последнее уравнение будет логично умножить на коэффициент  .
.
Тогда  , подставляя эту информацию в 1-е уравнение, получим
, подставляя эту информацию в 1-е уравнение, получим 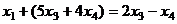 , тогда
, тогда  .
.
Запишем общее решение  ,
, 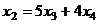 ,
,
оно же в векторном виде: 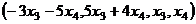 .
.
Поочерёдно присваивая 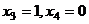 , затем
, затем 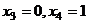 , получим два вектора: (-3,5,1,0) и (-5,4,0,1).
, получим два вектора: (-3,5,1,0) и (-5,4,0,1).
Ответ. Общее решение  ,
,  .
.
ФСР (-3,5,1,0) и (-5,4,0,1).
Задача 25.
Решить однородную систему, найти ФСР 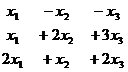
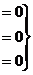
Решение.
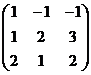
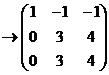
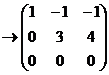 ранг = 2.
ранг = 2.
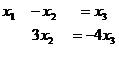
Тогда  , подставим в 1-е:
, подставим в 1-е:  ,
,  .
.
Ответ. Общее решение:  ,
,  , ФСР:
, ФСР: 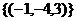 .
.
Задача 26 запасная
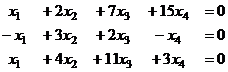
Решение.
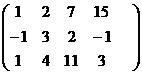







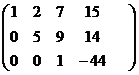
Система уравнений: 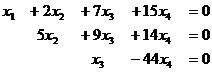
Базисный минор в 1,2,3 столбцах, свободная переменная х4.
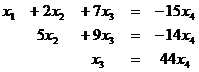
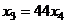 подставим во 2-е:
подставим во 2-е: 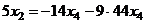 =
=  =
= 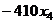 , это
, это  тогда
тогда  .
.
Далее,  =
= 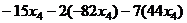 =
=
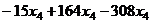 =
= 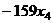 .
.
Итак, общее решение 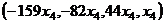 .
.
ФСР состоит из одного вектора 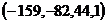 .
.
Проверка, подставим в систему:
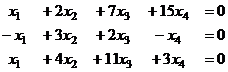
Практика 12. (16 дек 932025, 19 дек 932024).
Задача 27 (повт). 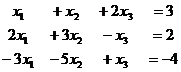
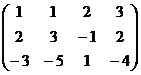
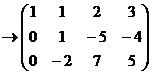
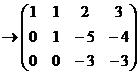
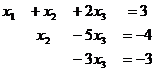 тогда
тогда 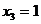 ,
,  ,
, 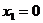 .
.
Ответ (0,1,1).
Повторение и контрольная работа по системам уравнений:
1) Определённая.
2) Неоднородная неопределённая
3) Однородная неопределённая.
(60-80 минут, почти вся пара).
Практика 13. (22 дек 932025, 24 дек 932024)
Задача 28. Найти наименьшее натуральное число k, при котором решение системы единственно:

Решение. Для существования и единственности решения системы с основной квадратной матрицей A необходимо и достаточно, чтобы матрица A являлась невырожденной.
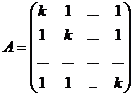 вырождена при k=1, так как все строки совпадают,
вырождена при k=1, так как все строки совпадают,
Рассмотрим при 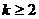 . Прибавим все столбцы к первому (все числа в 1-м столбце окажутся равны
. Прибавим все столбцы к первому (все числа в 1-м столбце окажутся равны 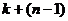 ), вынесем общий множитель за знак определителя.
), вынесем общий множитель за знак определителя.
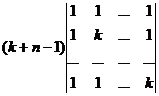
Затем вычтем 1-й столбец из всех остальных. С помощью таких действий получим: = 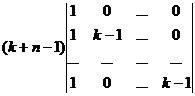 =
=  при
при 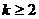 .
.
Таким образом, наименьшее натуральное число с таким условием  .
.
Задача 29. Найти решение системы 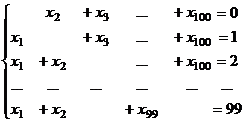
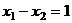 ,
, 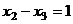 , ...
, ... 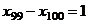 .
.
Арифметическая прогрессия.
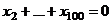 , Следовательно,
, Следовательно, 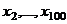 , образуют посл-сть
, образуют посл-сть
k, k-1, …, 1,0, -1, … , -k , при 99 элементах: 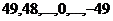 .
.
Ответ.  .
.
Задача 30. Пусть  таковы, что
таковы, что
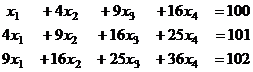
Найти 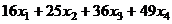 .
.
Решение.
Запишем исходную систему уравнений в виде:
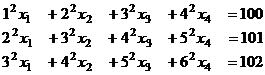
Проверим, может ли 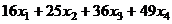 =
=  быть линейной комбинацией уравнений этой системы.
быть линейной комбинацией уравнений этой системы.
Если проверять на вырожденность минор 3 порядка, то получалось бы
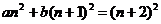
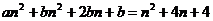

Система: 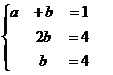 Несовместна.
Несовместна.
Для минора 4 порядка:

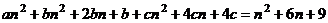 ,
,
 ,
,
это приводит к системе
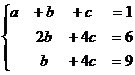
Из разности 2-го и 3-го получаем  , тогда
, тогда  ,
, 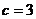 . Тогда из 1-го
. Тогда из 1-го 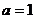 .
.
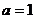 ,
,  ,
, 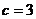
Тогда  =
=  .
.
Задача 31. Даны 3 вектора:  . Доказать, что они образуют базис в пространстве, и найти координаты вектора
. Доказать, что они образуют базис в пространстве, и найти координаты вектора 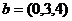 в новом базисе.
в новом базисе.
Решение. Вычисляя определитель, получим, что он отличен от 0.
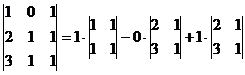 =
= 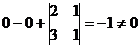 .
.
Затем ищем новые координаты вектора.
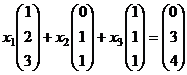 система:
система: 
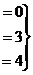
Здесь удобнее получить треугольную структуру ниже не главной, а побочной диагонали. Ведь в третьем столбце все числа 1. 

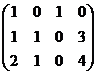

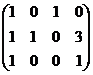 .
.
Система: 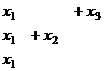
 . Из 3-го уравнения
. Из 3-го уравнения  .
.
Тогда из 2-го 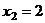 , а из 1-го уравнения:
, а из 1-го уравнения: 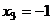 .
.
Мы поочерёдно выразили их, начиная с 1-го а не последнего, так как нули ниже побочной, а не главной диагонали. Такая модификация метода Гаусса также возможна.
Ответ. Координаты в новом базисе  .
.
- - - Перерыв - - -
Задача 32. Даны 3 вектора: 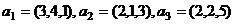 . Доказать, что они образуют базис в пространстве, и найти новые координаты вектора
. Доказать, что они образуют базис в пространстве, и найти новые координаты вектора 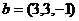 .
.
Решение. Сразу начнём решать систему, тогда невырожденность основной матрицы и факт наличия нового базиса установим заодно в процессе преобразований методом Гаусса.
 система:
система: 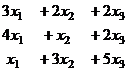

Умножим на 2 третье уравнение, чтобы начать метод Гаусса с 3-го столбца:
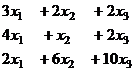
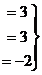
Расширенная матрица 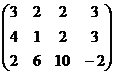
Отнимем от 2-й строки 1-ю, а от 3-й 5-кратную первую.
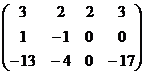
теперь от 3-й строки 4-кратную 2-ю.
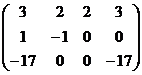
Из последнего уравнения  , тогда из 2-го
, тогда из 2-го 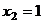 .
.
Из 1-го  ,
,  ,
, 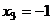 .
.
Ответ. Координаты в новом базисе 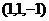 .
.
Проверка: 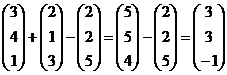 .
.
Задача 33. Пусть в линейном пространстве многочленов степени не выше 3, задан базис 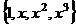 и система функций
и система функций 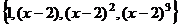 . Построить матрицу перехода, установить, что новая система тоже образует базис, и разложить многочлен
. Построить матрицу перехода, установить, что новая система тоже образует базис, и разложить многочлен  по основанию
по основанию 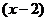 .
.
Решение. Пусть  .
.
Тогда 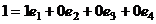 ,
,

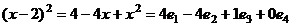
 .
.
Построим матрицу перехода:
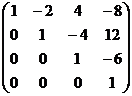
она невырождена, т.к. определитель равен 1.
Система уравнений:
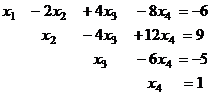
Тогда 
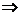
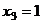
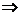
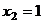
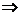
 .
.
Новые координаты (0,1,1,1).
Таким образом,  =
= 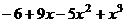 =
=
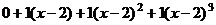 =
= 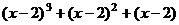 .
.
Ответ. 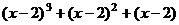 .
.
Задача 34. Выразить вектор  через систему векторов
через систему векторов
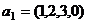 ,
, 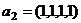 ,
, 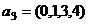 ,
,  , и установить, является ли система является базисом в
, и установить, является ли система является базисом в 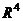 .
.
Решение. Если вектор  можно выразить, то:
можно выразить, то:
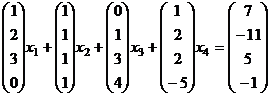
Это приводит к системе уравнений:
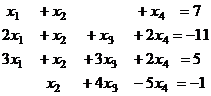
Построим расширенную матрицу и преобразуем её.
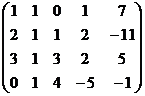



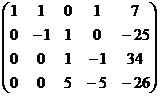


Ранг основной матрицы равен 3, а расширенной 4.
Система несовместна. 4 вектора не образуют базис, они ЛЗС и образуют 3-мерное подпространство, причём вектор  в нём не содержится. Выразить его через эту систему векторов невозможно.
в нём не содержится. Выразить его через эту систему векторов невозможно.
Решая систему с 4 столбцами, можно найти выражение 4-го вектора через первые 3: 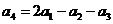 .
.
Задача 35. Доказать, что множество матриц
A = 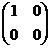 , B =
, B =  , C =
, C = 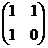 , D =
, D = 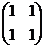 образует базис в линейном пространстве всех матриц порядка 2.
образует базис в линейном пространстве всех матриц порядка 2.
Решение.
Мы знаем, что в этом пространстве есть базис
 =
= 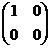 ,
,  =
= 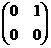 ,
, 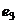 =
=  ,
,  =
=  .
.
Построим матрицу перехода.
A =  , B =
, B =  +
+  , С =
, С =  +
+  +
+ 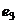 , D =
, D =  +
+  +
+ 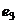 +
+  .
.

эта матрица невырождена, определитель равен 1. Система из 4 элементов ЛНС в 4-мерном пространстве, значит, базис.
Задача 36. При каком условии множество матриц
A = 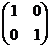 , B =
, B =  , C =
, C = 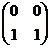 , D =
, D = 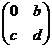 образует базис в линейном пространстве всех матриц порядка 2 ?
образует базис в линейном пространстве всех матриц порядка 2 ?
Решение.
 =
= 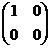 ,
,  =
= 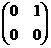 ,
, 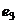 =
=  ,
,  =
=  .
.
A =  +
+  , B =
, B =  +
+ 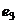 , С =
, С = 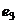 +
+  , D =
, D = 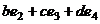 .
.
Строим матрицу перехода.

Нужно, чтобы определитель был не равен 0.
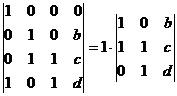 =
= 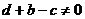 .
.
Таким образом, условие:  .
.
Практика 14. (23 дек 932025, 26 дек 932024)
Задача 37. Построить матрицу квадратичной формы.
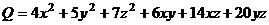 .
.
Решение. Коэффициенты 4,5,7, которые были при квадратах, располагаем по главной диагонали. Далее, поровну распределяем коэффициенты при попарных произведениях, например,
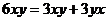 , тогда
, тогда 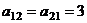 .
.
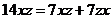 ,
, 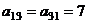 .
.
 , тогда
, тогда 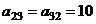 .
.
Тогда 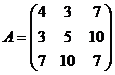 .
.
Проверка. 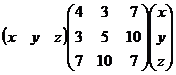 =
=
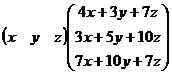 =
=
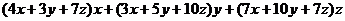 =
=
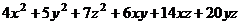 .
.
Задача 38. Найти косинус угла между векторами 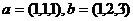 .
.
Решение. 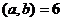 ,
, 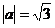 ,
,  ,
,
учитывая что 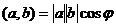 , то
, то 
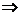
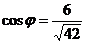 .
.
Ответ. 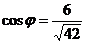 .
.
Задача 39. Найти косинус угла между векторами 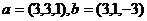 .
.
Решение. 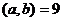 ,
, 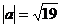 ,
,  ,
,
учитывая что 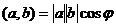 , то
, то 
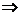
 .
.
Оценим приблизительно, какой это угол. Заметим, что если было бы 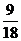 то было бы
то было бы 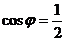 и угол 600.
и угол 600.
В данном случае косинус чуть меньше, а значит угол чуть больше 600.
Ответ.  .
.
Поиск скалярных произведений без координат.
Задача 40. Векторы a,b выражены через базис p,r: 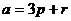 ,
, 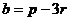 .
. 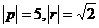 , угол между ними 45 градусов. Найти
, угол между ними 45 градусов. Найти 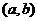 .
.
Решение. 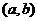 =
=  =
=  .
.
Далее, так как 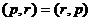 то объединим их, и получим
то объединим их, и получим 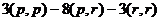 =
=
 =
= 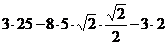 =
=  . Ответ. 29.
. Ответ. 29.
Задача 41. Векторы a,b выражены через p,r: 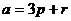 .
. 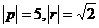 , угол между ними 45 градусов. Найти
, угол между ними 45 градусов. Найти  .
.
Решение.
 =
=  =
= 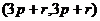 =
=  =
=
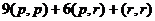 =
= 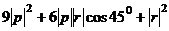 =
=
 =
=  = 257.
= 257.
Ответ. 257.
Задача 42. Векторы a,b выражены через p,q: 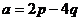 ,
, 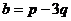 .
.  , угол между ними 600. Найти
, угол между ними 600. Найти 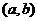 .
.
Решение.
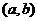 =
= 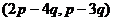 =
= 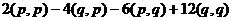 =
= 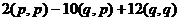 =
= 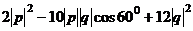 =
=
 =
= 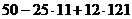 = 1227.
= 1227.
Ответ. 1227.
Задача 43. Ортогонализовать систему векторов.
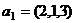 ,
,  ,
, 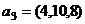 .
.
Решение. 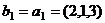 .
.
Построим вектор 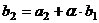 , так, чтобы он был ортогонален
, так, чтобы он был ортогонален  .
.
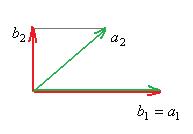
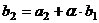 , причём
, причём 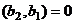 . Тогда
. Тогда
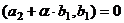 то есть
то есть  , тогда
, тогда  .
.
Таким образом, 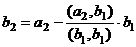 .
.
В случае данной задачи,  =
= 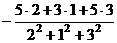 =
=  .
.
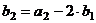 =
= 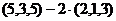 =
= 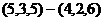 =
= 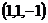 .
.
Проверим, что он действительно ортогонален  .
.
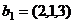 ,
,  ,
,  .
.
Теперь ищем 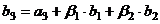 , причём так, чтобы
, причём так, чтобы 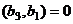 и
и  . В теории доказано, что
. В теории доказано, что 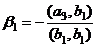 ,
, 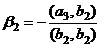 .
.
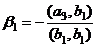 =
= 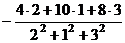 =
= 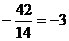 ,
,
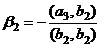 =
= 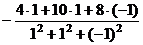 =
= 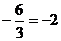 .
.
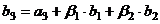 =
= 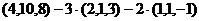 =
=
 =
= 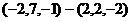 =
= 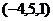 .
.
Получившийся вектор 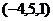 ортогонален каждому из векторов
ортогонален каждому из векторов  (если скалярно умножить, получится 0).
(если скалярно умножить, получится 0).
Ответ. 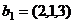 ,
, 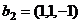 ,
, 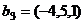 .
.
P.S. Покажем, что определитель не изменился.
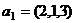 ,
,  ,
, 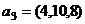 .
.
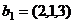 ,
, 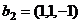 ,
, 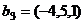 .
.
 = 48 + 20 + 150 - 36 – 100 – 40 = 8 + 50 – 16 = 42.
= 48 + 20 + 150 - 36 – 100 – 40 = 8 + 50 – 16 = 42.
 = 2 + 15 + 4 – (-12) – (-10) – 1 = 21 +12 + 10 – 1 = 42.
= 2 + 15 + 4 – (-12) – (-10) – 1 = 21 +12 + 10 – 1 = 42.
Прочие теоретические задачи на разные темы.
Задача 44. Доказать, что определитель кососимметрической матрицы нечётного порядка равен 0.
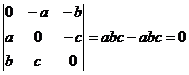
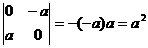
Решение.
Во-первых,  .
.
Если матрица кососимметрическая, то  .
.
Напр., 
Тогда 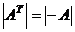 , при этом
, при этом 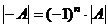
(коэффициент  вынесли из n строк).
вынесли из n строк).
В итоге,  .
.
Если n нечётно, то 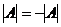 , то есть
, то есть  .
.
Задача 45. На плоском листе нарисован график функции 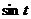 , затем лист свёрнут в цилиндр радиуса 1 вокруг оси Z так, чтобы совпали точки, отличающиеся на
, затем лист свёрнут в цилиндр радиуса 1 вокруг оси Z так, чтобы совпали точки, отличающиеся на  . Доказать, что все точки графика окажутся в одной плоскости.
. Доказать, что все точки графика окажутся в одной плоскости.
Решение.
То что получается какая-то замкнутая кривая ещё не гарантирует, что она будет располагаться в плоскости, так, например, может быть обруч или колесо, изогнутое в 3-мерном пространстве, так что все точки не будут в одной плоскости.
Пусть исходный график лежит в плоскости параметров 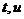 , график
, график  . Преобразование координат при таком переходе от плоскости параметров (
. Преобразование координат при таком переходе от плоскости параметров ( 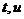 ) к пространственным координатам (
) к пространственным координатам ( 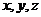 ) задаётся так:
) задаётся так: 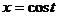 ,
, 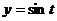 ,
, 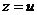 .
.
Таким образом, указанная кривая переходит в пространственную кривую, заданную параметрически:
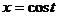 ,
, 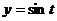 ,
, 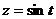 .
.
чтобы доказать, что все её точки в одной плоскости, достаточно фиксировать какие-либо 2 точки с наиболее простыми координатами и затем доказать, что произвольная третья при любом t попадёт в ту же плоскость, то есть 3 радиус-вектора будут в одной плоскости. Проверить это можно с помощью равенства 0 определителя из этих радиус-векторов.
Пусть две точки соответствуют 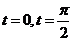 , а третья произвольному t.
, а третья произвольному t.
Тогда определитель из трёх радиус-векторов:
 =
= 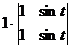 = 0 так как этот минор 2 порядка вырожден.
= 0 так как этот минор 2 порядка вырожден.
Таким образом, при произвольном t точка окажется в плоскости первых двух векторов, в итоге все точки фигуры - в одной плоскости.
Задача 46. Докажите, что определитель 3-диагональной матрицы с 1 на главной диагонали и непосредственно над ней и  непосредственно под ней является числом Фиббоначи.
непосредственно под ней является числом Фиббоначи.
Решение.


Разложим по 1-й строке. Два минора имеют такое строение:
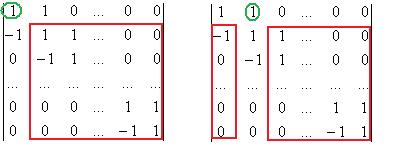
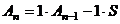 , где
, где 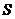 минор, в 1-м столбце которого только одно
минор, в 1-м столбце которого только одно  в углу и 0 на остальных местах.
в углу и 0 на остальных местах. 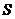 разложим по его 1 столбцу.
разложим по его 1 столбцу.
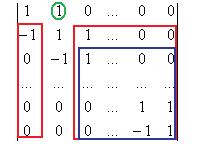
Тогда там остаётся минор той же структуры, но порядка 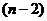 .
.
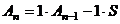 =
= 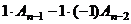 =
= 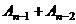 .
.
Итак, 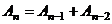 . Числа Фиббоначи (
. Числа Фиббоначи (  )
)
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
| 
| 
| 
| 
|
| 1 | 2 | 3 | 5 | 8 |
Контрольные задачи (1 семестр)
1. Алгебраические операции, проверка комм., асс., нейтр. элемент.
2. Система уравнений в поле вычетов.
3. Умножение матриц.
4. Определители.
5.Обратная матрица.
6. Ранг матрицы.
7. Система линейных уравнений.
8. Неопределённая система.
9. Однородная система.
Дата добавления: 2021-01-20; просмотров: 52; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
