Построение частотных характеристик
Московский Государственный Технический Университет
Им. Н. Э. Баумана
Конспект СЕМИНАРОВ по курсу
„Управление Техническими Системами”
( Учебное пособие для студентов третьего курса )
Б.Г. Кулешов
Г.Н.Товарных
Москва - 2010
1. Построение временных характеристик
1.1. Колебательное звено.
; 
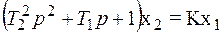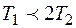(5.11)
Корни характеристического уравнения:
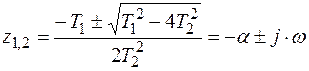(5.12)
где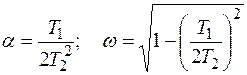 
Решение однородного уравнения имеет вид:
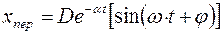
Частное решение при единичном скачке:
.
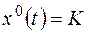Тогда общее решение (в нашем случае переходная функция) равно:
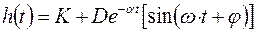(5.13)
Найдем первую производную:
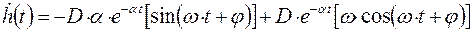
Используя нулевые начальные условия, получим:
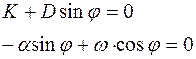
Откуда: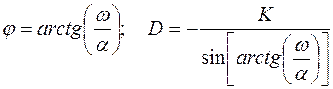 
Подставляя полученные компоненты в (5.13) получим:
|
|
|
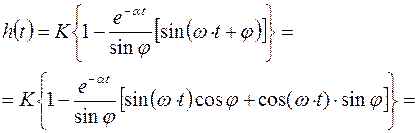
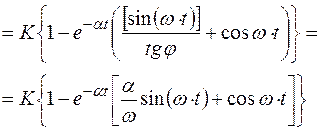(5.14)
Можно получить (5.14) также следующим образом.
Решение однородного уравнения запишем в виде
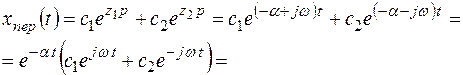
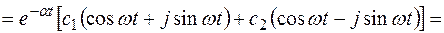
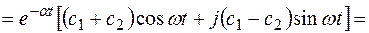
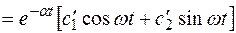
где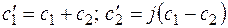 
.
Полное решение уравнения при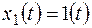 
можно записать в виде
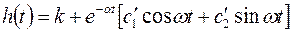
Продифференцируем полученное решение
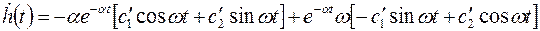
При нулевых начальных условиях получаем
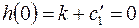
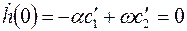
откуда
; 
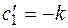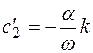
Окончательно временная функция имеет вид
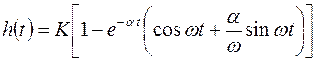
График временной характеристики представлен на рис.5.3.
|
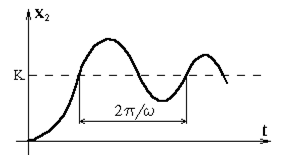
Рис.5.3
1.2. Гармоническое звено.
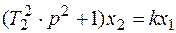(5.15)
Корни характеристического уравнения:
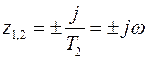
Тогда вместо (5.13) можно записать:
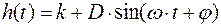
Откуда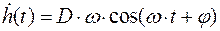 
При нулевых начальных условиях имеем
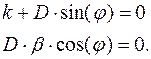
Из второго условия получаем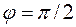 
, а из первого 
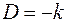. Тогда
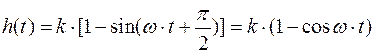(5.16)
Соответствующая кривая изображена на рис.5.4.
|
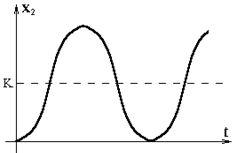
Рис.5.4
1.3. Неустойчивое апериодическое звено первого порядка .
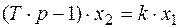(5.17)
Корень характеристического уравнения: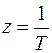 
Общее решение имеет вид: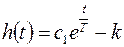 
При нулевом начальном условии получаем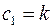 
.
|
|
|
Тогда
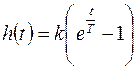(5.18)
Вид временной характеристики показан на рис.5.5.
|
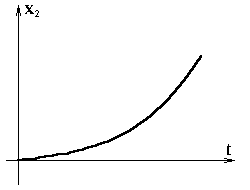
Рис.5.5
1.4. Идеальное дифференцирующее звено.
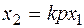(5.19)
При единичном скачке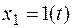 
, получим (рис.5.6).
|
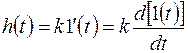
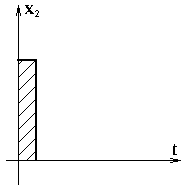
Рис.5.6
1.5. Идеальное звено с введением производной.
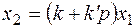(5.20)
При 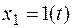можно записать
|
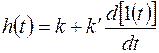
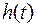показан на рис.5.7.
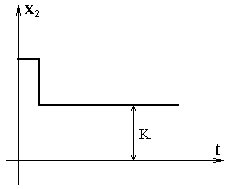
Рис.5.7
1.6. Идеальное интегрирующее звено.
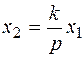(5.21)
Для входного сигнала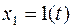 
получим (рис.5.8).
|
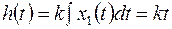
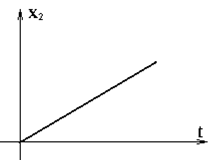
Рис.5.8
1.7. Интегрирующее звено с запаздыванием.
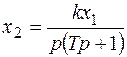(5.22)
Запишем это уравнение в следующем исходном виде:
|
|
|
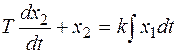
Решение однородного уравнения
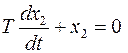
имеет вид:
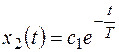
Частное решение при единичной функции на входе получается равным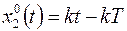 
Общее решение имеет вид
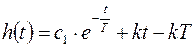
Используя нулевые начальные условия, получим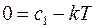 
Тогда общее решение принимает вид (рис.5.9)
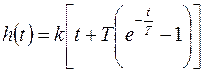(5.23)
|
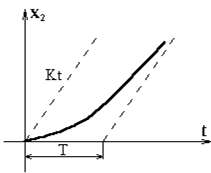
Рис.5.9
1.8. Дифференцирующее звено с замедлением.
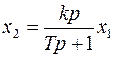(5.24)
В дифференциальной форме можно записать
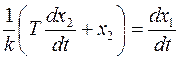
При 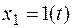получим
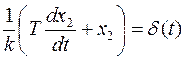
Таким образом требуется найти весовую функцию. Найдем ее как производную от переходной функции, которая равна (смотри переходную функцию апериодического звена первого порядка)
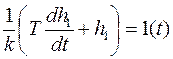
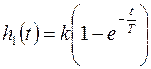
Весовая функция равна производной от переходной функции, тогда имеем
для переходной функции уравнения (5.24) (рис.5.10)
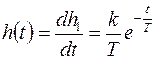(5.25)
|
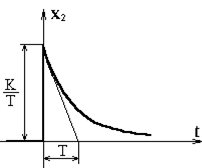
Рис.5.10
1.9. Интегральное звено с введением интеграла.
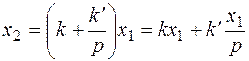(5.26)
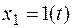При получим
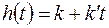(5.27)
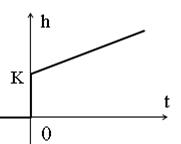
Вид линейной зависимости (5.27) показан на рис.5.11.
|
|
|
Рис. 5.11.
1.10. Идеальное звено с запаздыванием.
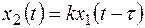(5.28)
Для единичного скачка 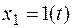временная характеристика (5.28) показана на рис.5.12.
 |
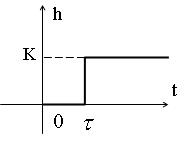Рис.5.12.
1.11. Идеальное простое звено.
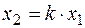(5.29)
Временная характеристика показана на рис.5.13.
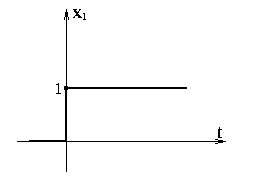
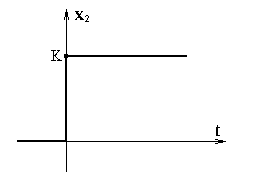
Рис.5.13
1.12. Система автоматического регулирования описывается уравнением
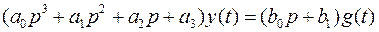, (1)
где
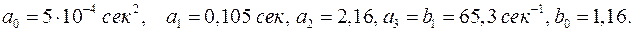
Найти переходный процесс для двух случаев:
1. При включении системы после, ее предварительного рассогласования на величину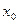 
.
2. При управляющем воздействии в виде единичной ступенчатой функции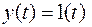 
и нулевых начальных условиях 
.
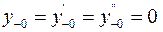1. Решение для случая 1.
Характеристическое уравнение, соответствующее (1), имеет при заданных коэффициентах вид
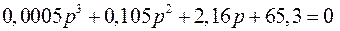. (2)
Корни уравнения (2) могут быть найдены каким-либо из известных методов. Эти корни равны
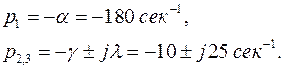(3)
Выходная величина системы, характеристическое уравнение которой имеет один вещественный и пару комплексных корней, имеет вид
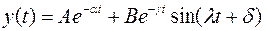. (4)
Начальные условия равны
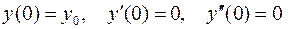. (5)
Из (4) находим
,
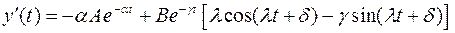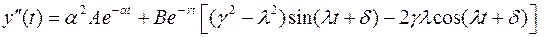. (6)
Из выражений (4)—(6) получаем систему уравнений для определения постоянных интегрирования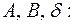 
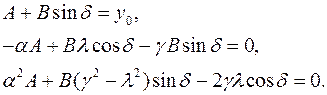(7)
После подстановки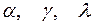 
согласно (3) найдем
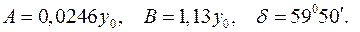
Подстановка (8) в (4) дает решение задачи:
.
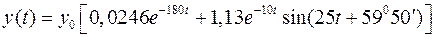Этот результат можно получить непосредственно из (2) и (5), если воспользоваться приложением 10.
2. Указание к решению задачи для второго случая. Начальные условия, имеющие место непосредственно после приложения ступенчатого воздействия, могут быть определены при помощи приложения 9.
Ответ.
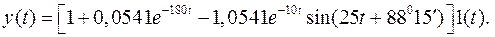
Построение частотных характеристик
2 .1. Идеальное простое звено .
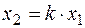
Передаточная функция имеет вид:
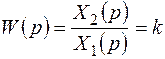(6.2)
Тогда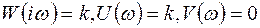 
Передаточная функция изображается на комплексной плоскости в виде точки (рис.6.1).
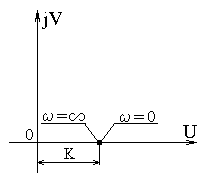
Рис.6.1
2.2. Идеальное дифференциальное звено .
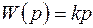(6.3)
Подставляя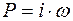 
, получим
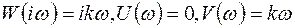
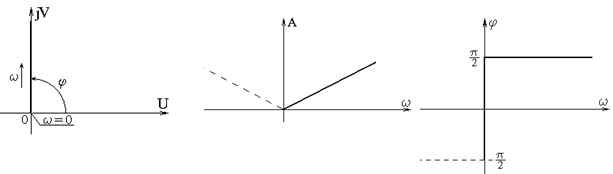
Для амплитуды и фазы справедливы соотношения: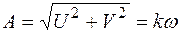 
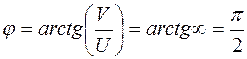
Полученные зависимости показаны на рис.6.2. Пунктирным линиям соответствуют значения при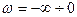 
.
Рис.6.2
Видно, что введение производной в закон регулирования создает опережение по фазе на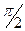 
.
2.3. Идеальное интегрирующее звено .
Получаем
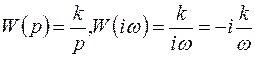(6.4)
Тогда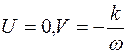 
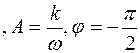
Характеристики данного звена показаны на рис.6.3. Введение интеграла в закон регулирования создает запаздывание по фазе на угол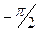 
.
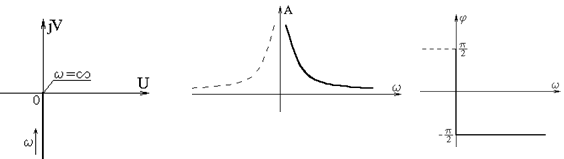
Рис.6.3
2.4. Идеальное звено с введенной производной.
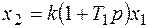(6.32)
Частотная передаточная функция имеет вид
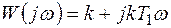(6.33)
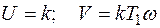
Амплитуда и фаза соответственно равны
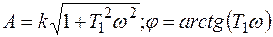
На рис.6.10 показаны частотные характеристики звена. Амплитудная логарифмическая частотная характеристика находится из выражения
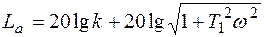
и имеет вид (рис.6.11).
Рис.6.10
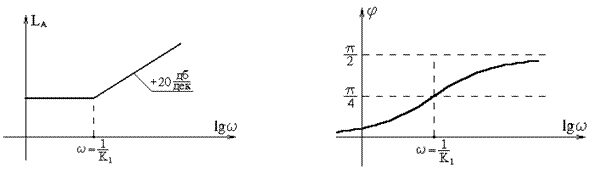
Рис.6.11
2.5. Инерционное дифференцирующее звено.
Уравнение и передаточная функция звена записывается в виде
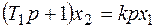(6.34)
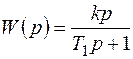(6.35)
Подставляя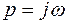 
, получим частотную передаточную функцию
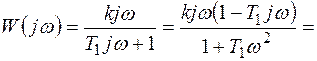
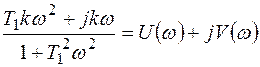
Здесь
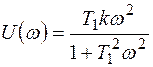(6.36 а) 
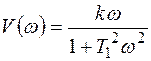(6.36 б)
Тогда для амплитуды и фазы получаем
; 
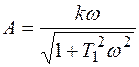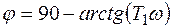
Возведем (6.36 б) в квадрат, а из (6.36 а) выразим
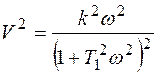(6.37) 
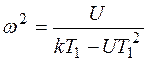(6.38)
Избавимся в уравнении (6.37) от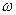 
= 
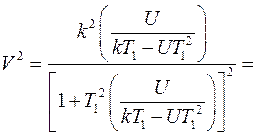
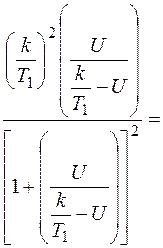
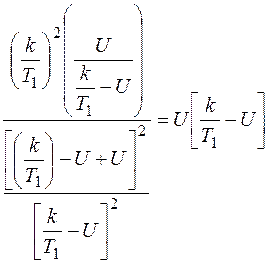
или
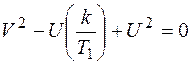
Приведем полученное выражение к виду
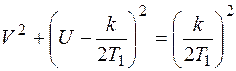(6.39)
Таким образом, АФЧХ звена представляет собой полуокружность радиусом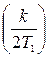 
(рис.6.12).
Логарифмическая амплитудно-частотная характеристика имеет вид:
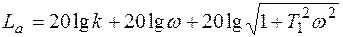(6.40)
и может быть построена как сумма трех характеристик (рис.6.13).
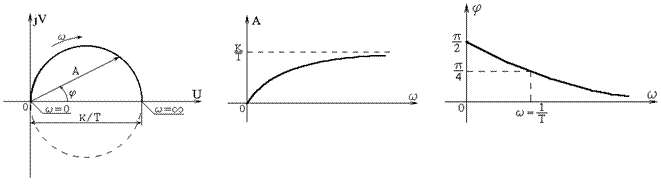
Рис.6.12
 |
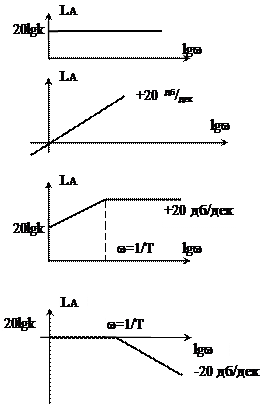Рис.6.13.
2.6. Интегрирующее звено с запаздыванием.
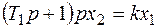(6.42)
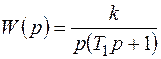(6.43)
Найдем частотную передаточную функцию
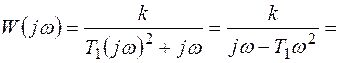
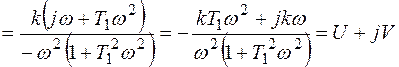(6.44)
Здесь
; 
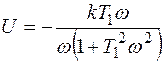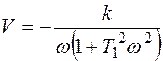
Для амплитуды и фазы получаем соотношения
;
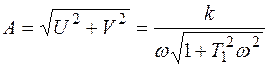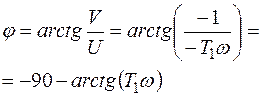
АФЧХ звена представлены на рис.6.15.
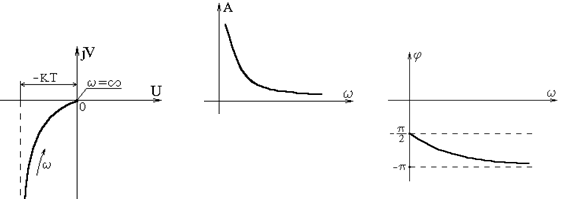
Рис.6.15
Логарифмическая амплитудная характеристика имеет вид
 |
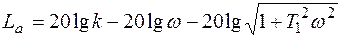
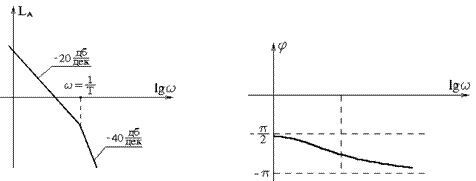Рис.6.16
2.7. Простое гармоническое звено.
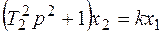(6.45)
; 
;
; 
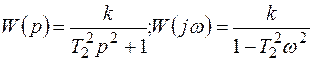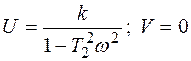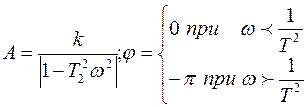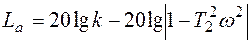
Амплитуда и фаза при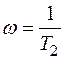 
терпят разрыв (рис.6.17)
 |
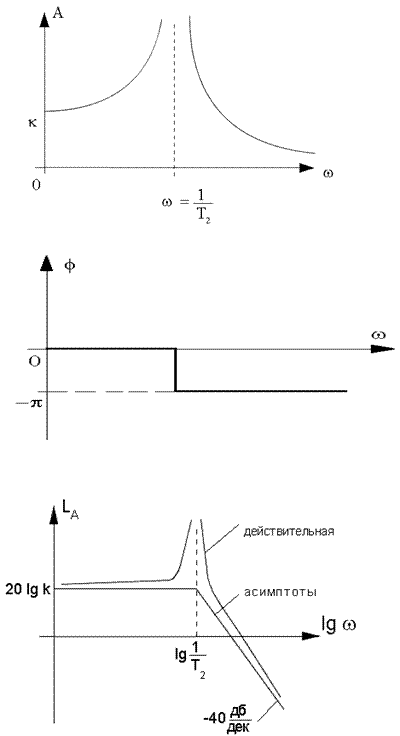Рис.6.17.
Таблица 4.2
Обычные логарифмические частотные характеристики элементарных множителей (Кузовков)
| № по пор. | Вид сомножителя | Годограф в полярной системе координат | Логарифмические амплитудная и фазовая характеристики |
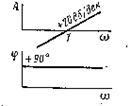
| 1 | J w |
| 
|
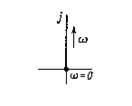
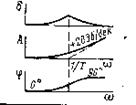
| 2 | Tj w +1 |
| 
|
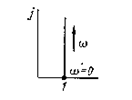
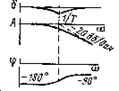
| 3 | T 2 ( j w )2+2 z Tj w +1 |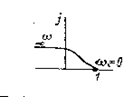 
| 
|
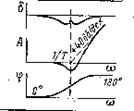
| 4 | T2(j w )2+1 | 
| 
|
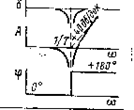
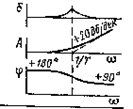
| 5 | Tj w -1 |
| 
|
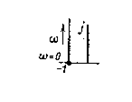
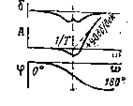
| 6 | T2(j w )2-2 z Tj w +1 |
| 
|
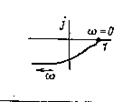
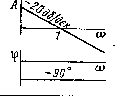
| 7 |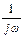 
|
| 
|
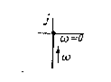
| 8 |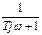 
|
| 
|
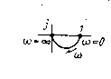
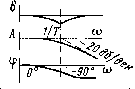
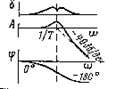
| 9 |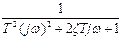 
|
| 
|
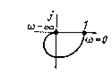
| 10 |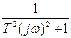 
|
| 
|
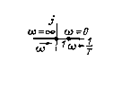
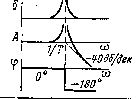
| 11 |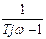 
|
| 
|
| 12 |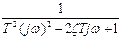 
|
| 
|
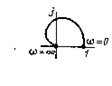
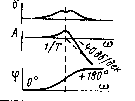
Таким образом, логарифмические амплитудно-частотную и фазо-частотную характеристики всех множителей
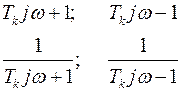
можно построить без всякого расчета при помощи двух шаблонов, вырезанных из прозрачного материала: один — по форме графика поправки d, а другой — по форме логарифмической фазо-частотной характеристики j множителя Tkj w+1. Эти шаблоны можно изготавливать, например, в масштабах (4.22) (см. приложение V).
2.8. Построить амплитудно-фазовую характеристику цепи RC , представленной на рис. 30а; R =1 кОм, C =10 мкф.
 |
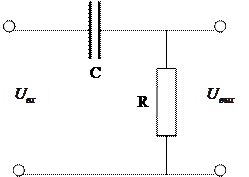Рис. 30 а
Решение. Частотная передаточная функция цепи равна
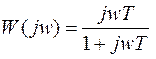, (1)
где T=RC=103*10-5=10-2 сек.
Преобразуем выражение (1) таким образом, чтобы оно представляло собой комплексное число в алгебраической форме:
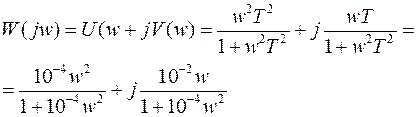(2)
Задаваясь отдельными значениями w, можно по формуле (2) вычислить ряд пар значений U(w) и V(w) и построить по ним амплитудно-фазовую характеристику цепи.
Однако анализ выражения (2) показывает , что эта характеристика определяется уравнением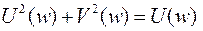 
и для положительных частот является полуокружностью, расположенной в верхней полуплоскости с центром в точке (0,5;j0) и радиусом 0,5 (рис. 30,б).
Из выражения (2) видно, что при w=0 W(jw)=0+j0, а при w=¥ W(jw)=1+j0. Точки, соответствующие этим, а также некоторым промежуточным частотам, указаны на рис. 30,б; значения частоты на этом и всех последующих рисунках даны в рад/сек.
 |
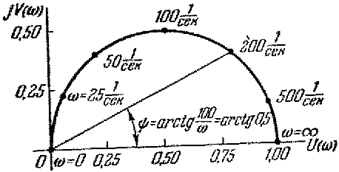Рис. 30 б. Амплитудно-фазовая характеристика дифференцирующего звена (случай 1).
Частоты, соответствующие промежуточным точкам кривой, могут быть найдены следующим образом.
Аргумент комплексного числа (2) равен
y = argW ( jw ) = arctg (1/ wt ) = atctg (100/ w ), (3)
поэтому луч, проведенный из начала координат под углом y к оси абсцисс, пересекает амплитудно-фазовую характеристику в точке, в которой величина w определяется через y согласно (3). Один такой луч показан на рисунке.
2.9. Найти уравнения кривой, представляющей собой амплитудно-фазовую характеристику дифференцирующего звена, изображенного на рис. 32,а.
Построить амплитудно-фазовую характеристику звена для случая R1=40 кОм, R2=10 кОм, С=2,5 мкф.
 |
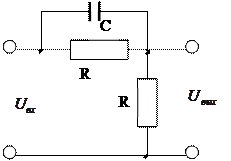Рис. 32 а.
Ответ. Уравнение кривой имеет вид
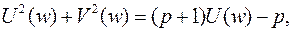(1)
где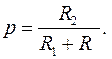 
Согласно (1) амплитудно-фазовая характеристика является для положительных частот полуокружностью, расположенной в верхней полуплоскости, с центром в точке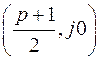 
и радиусом 
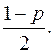Эта характеристика построена для указанных данных на рис. 32,б.
 |
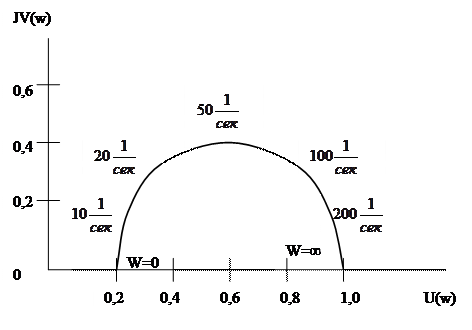Рис. 32 Амплитудно-фазовая характеристика дифференциального звена (случай 2).
Дата добавления: 2020-12-22; просмотров: 140; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!