Схема исследования функции на экстремум.
ЛЕКЦИЯ № 8
Раздел 2. Математический анализ.
Тема: Производная функции. Исследование функции с помощью производной.
Цели: обобщить свойства функции и методы ее исследования с помощью производной, составить алгоритм исследования функции на экстремум.
План.
1. Условия возрастания и убывания функции.
2. Экстремум функции.
3. Схема исследования функции на экстремум.
Условия возрастания и убывания функции.
Вспомним определение возрастающей и убывающей функции на множестве Х.
Функцию y=f(x) называют возрастающей на множестве Х, если с ростом аргумента, растет значение функции.
Функцию y=f(x) называют убывающей на множестве Х, если с ростом аргумента, значения функции уменьшаются.
Рассмотрим теоремы, которые устанавливают связь между возрастанием и убыванием функции и знаком производной на заданном интервале.
Теорема 1.
Пусть функция y=f(x) непрерывна на интервале (a;b) и дифференцируема на интервале (a;b) . Для того, чтобы эта функция на этом интервале не убывала (не возрастала), необходимо и достаточно, чтобы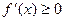 
( 
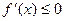) для всех хє (a;b) .
Утверждению теоремы можно дать геометрическую интерпретацию:
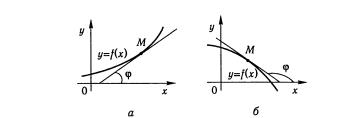
Рис.5.
Касательные к графику возрастающей функции образуют с положительным направлением оси Ох острые углы φ (рис. 5 а ), тангенс этого угла неотрицательный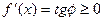 
.
В случае убывающей функции углы φ тупые (рис.5 б), тангенс этого угла неположительный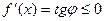 
.
|
|
|
Теорема 2.
Если в каждой точке интервала (a;b) выполняется условие
( )
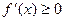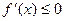причем точки, в которых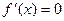 
, не образуют ни какого отрезка, то функция y=f(x) возрастает (убывает) на этом интервале.
Интервалы возрастания и убывания функции называются интервалами монотонности.
Исследование функции на монотонность можно провести по такой
схеме:
1) Найти область определения функции;
2) Найти первую производную функции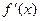 
;
3) Найти те значения х , в которых 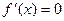, или не существует.
Это так называемые критические точки функции, они разбивают область определения функции на интервалы, на которых первая производная сохраняет знак.
4) Исследовать знак первой производной на каждом из таких интервалов. Если 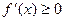, то функция возрастает на этом интервале.
Если 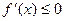, то функция убывает.
Экстремум функции.
Мы установили, что в точках, где производная положительная, функция возрастает, а в точках, где производная отрицательная, функция убывает.
Осталось рассмотреть точки, в которых производная равна нулю, или не существует. Эти точки называются критическими.
Если функция непрерывна на некотором промежутке и изменяется не монотонно, а, например, сначала возрастает, а потом убывает, то очевидно, что существуют такие значения функции, которые в сравнении с соседними значениями будут или наибольшими, или наименьшими. Такие значения функции соответственно называют максимальными и минимальными.
|
|
|
.
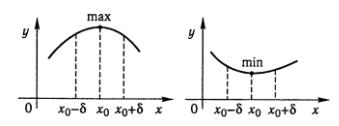
Рис.6.
Точку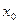 
называют точкою максимума функции, если для всех х из некоторой окрестности точки 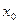, выполняется неравенство 
.
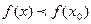Точку 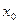называют точкой минимума функции, если для всех х из некоторой окрестности точки 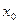, выполняется неравенство 
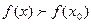.(Рис.6)
Теорема 3.
Если функция y=f(x) в точке 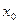имеет экстремум и производную, то 
.
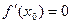Геометрически это означает, что касательная к кривой в этих точках параллельна оси Ох.
Но рассмотренная теорема не имеет обратной. Не при всех значения х, при которых производная равна нулю, функция имеет экстремум, например у=х ³.
Критические точки, в которых производная равна нулю называют стационарными. Точки экстремума дифференцированной функции нужно искать среди стационарных точек, или точек, где функция не имеет производной..
Теорема 4.
Если производная непрерывной функции при переходе через критическую точку 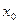изменяет знак, то в этой точке функция имеет экстремум. Максимум, если знак производной изменяется с плюса на минус, а минимум, если изменяется с минуса на плюс.
|
|
|
Теорема 5.
Пусть функция дифференцируема в окрестности стационарной точки 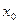, а в самой точке имеет вторую производную. Тогда, если 
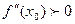, то в этой точке 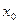функция имеет минимум. Если 
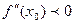, то в точке 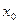функция имеет максимум.
Схема исследования функции на экстремум.
Рассмотрим схему исследования функции на экстремум с помощью первой производной.
Схема 1.
1) Найти область определения функции;
2) Найти первую производную ;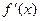
3) Найти критические точки, решив уравнение 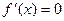и присоединить к ним те значения х, при которых 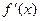не существует;
4) Исследовать знак производной при прохождении через каждую критическую точку по теореме 4, сделать выводы.
5) Записать координаты точек экстремумов.
Контрольные вопросы.
1. Какие функции называются монотонными?
2. Дать определение возрастающей и убывающей функции.
3. Как определить интервалы возрастания и убывания функции?
4. Какое необходимое условие существования экстремума функции в точке? 5. Как определяют экстремум функции?
6. Какой экстремум имеет функция в точке, если производная не поменяла знака, проходя через нее?
Литература:
В.П.Дубовик, И.И.Юрик «Высшая математика», К., 2003, ст.246-248.
|
|
|
Дата добавления: 2020-12-22; просмотров: 41; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!