Общее решение системы линейных уравнений
Решение систем линейных уравнений
Дана система 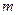 линейных уравнений с
линейных уравнений с  неизвестными:
неизвестными:
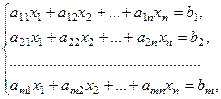
где 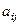 - коэффициенты, стоящие перед неизвестными;
- коэффициенты, стоящие перед неизвестными; 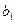 - свободные члены системы (
- свободные члены системы ( 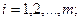
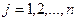 ).
).
Прямоугольная таблица чисел: 
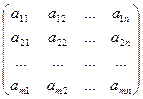 ,
,
составленная из коэффициентов, стоящих перед неизвестными, называется матрицей системы.
Матрица, получаемая приписыванием к матрице системы столбца свободных членов, называется расширенной матрицей:

Если ранг матрицы системы равен рангу расширенной матрицы, то такая система будет совместной. Совместной называется система, если она имеет хотя бы одно решение. Совместная система может иметь либо одно решение (называется определенной), либо бесконечно много решений (называется неопределенной). Система уравнений, не имеющая решений, называется несовместной. Если система уравнений содержит уравнение:
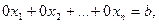
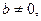
называемое противоречивым, то она несовместна.
Две системы, имеющие одни и те же решения, называются равносильными. Если в системе вычеркнуть одно или несколько уравнений:
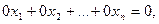
называемых тривиальными, то получим систему уравнений, равносильную исходной.
Рассмотрим решение системы уравнений тремя способами: по формулам Крамера, матричным способом и методом исключения неизвестных – методом Гаусса.
Формулы Крамера
Система линейных уравнений, имеющая число уравнений, равное числу неизвестных 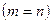 , и определитель матрицы системы, отличный от нуля, имеет единственное решение.
, и определитель матрицы системы, отличный от нуля, имеет единственное решение.
|
|
|
Определитель, элементами которого являются коэффициенты, стоящие перед неизвестными, называется определителем системы:
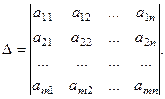
Вспомогательные определители: 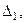
 …,
…,  составляются путем замены в определителе системы соответствующего столбца столбцом, состоящим из свободных членов:
составляются путем замены в определителе системы соответствующего столбца столбцом, состоящим из свободных членов:
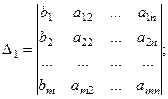


Решение системы уравнений находится по формулам Крамера:
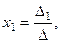
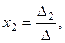 …,
…, 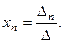
Если определитель системы 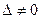 , то система имеет единственное решение (совместна и определенна). Если определитель системы
, то система имеет единственное решение (совместна и определенна). Если определитель системы 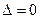 и все вспомогательные определители
и все вспомогательные определители 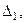
 …,
…,  также равны нулю, то такая система является совместной и имеет бесконечно много решений (неопределенна). Если определитель системы
также равны нулю, то такая система является совместной и имеет бесконечно много решений (неопределенна). Если определитель системы 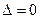 , но хотя бы один из вспомогательных определителей
, но хотя бы один из вспомогательных определителей 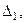
 …,
…,  отличен от нуля, то такая система не имеет решений (несовместна или противоречива).
отличен от нуля, то такая система не имеет решений (несовместна или противоречива).
Пример 3.1. Решить систему уравнений:

Решение. Вычислим определитель системы уравнений:
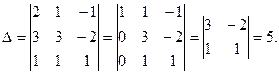
Определитель системы отличен от нуля, следовательно, система имеет единственное решение, которое можно найти по формулам Крамера.
Вычислим вспомогательные определители:
|
|
|
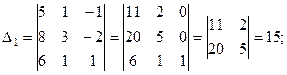
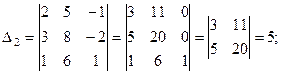

По формулам Крамера находим решение системы:
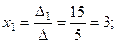
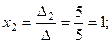
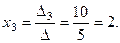
Матричный способ
Запишем матрицу системы, т.е. матрицу, состоящую из коэффициентов при неизвестных
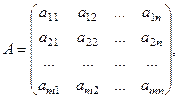
матрица, составленная из величин 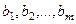 ,
, 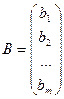 называется матрицей-столбцом свободных членов. Составим еще матрицу-столбец неизвестных:
называется матрицей-столбцом свободных членов. Составим еще матрицу-столбец неизвестных:

Тогда система уравнений в матричной форме примет вид:
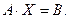
Если 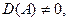 то получим решение матричного уравнения:
то получим решение матричного уравнения:
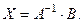
На данной формуле и основан матричный способ решения систем линейных уравнений.
Пример 3.2. Решить матричным способом систему уравнений:

Решение. Для данной системы

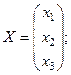
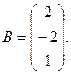
Матрица, обратная к матрице 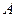 , имеет вид:
, имеет вид:
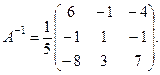
Подставляя в формулу для решения матричного уравнения, имеем:
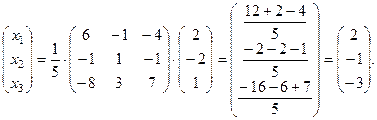
Таким образом, 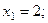

Метод исключения неизвестных – метод Гаусса
Рассмотрим систему m – линейных уравнений с n – неизвестными:

Суть метода Гаусса заключается в том, что с помощью элементарных преобразований расширенная матрица системы приводится к равносильной матрице ступенчатого (треугольного или трапецеидального) вида. Это и есть прямой ход метода Гаусса.
На основании полученной ступенчатой матрицы составляется новая система уравнений, равносильная исходной, из которой последовательно, начиная с последнего уравнения, находятся все неизвестные; это суть обратного хода метода Гаусса.
|
|
|
Матрица А называется ступенчатой, если она имеет вид:
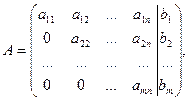 или
или 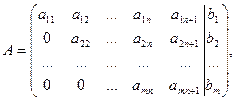
где  – числа, отличные от нуля.
– числа, отличные от нуля.
Элементарные преобразования матрицы:
1) отбрасывание строки, в которой все элементы равны нулю;
2) умножение всех элементов строки матрицы на число, не равное нулю;
3) изменение порядка строк матрицы;
4) прибавление к каждому элементу одной строки соответствующих элементов другой строки, умноженной на любое число.
Пример 3.3. Методом Гаусса решить систему уравнений:
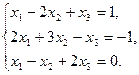
Решение. Расширенная матрица системы имеет вид:
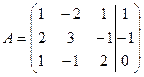 вычитая из элементов 3-й строки элементы 1-й, а из элементов 2-й строки элементы 1-й, умноженные на два, получим:
вычитая из элементов 3-й строки элементы 1-й, а из элементов 2-й строки элементы 1-й, умноженные на два, получим: 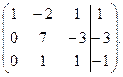 Вычтем из элементов 2-й строки элементы 3-й, умноженные на семь, и поменяем местами 2-ю и 3-ю строки:
Вычтем из элементов 2-й строки элементы 3-й, умноженные на семь, и поменяем местами 2-ю и 3-ю строки: 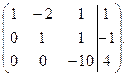 Запишем систему уравнений с новыми коэффициентами:
Запишем систему уравнений с новыми коэффициентами:
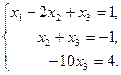
Применим обратный ход метода Гаусса:
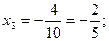
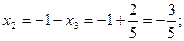
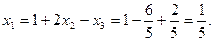
Решение системы: 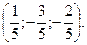
Общее решение системы линейных уравнений
Неизвестное 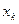 называется разрешенным, если какое-нибудь уравнение системы содержит
называется разрешенным, если какое-нибудь уравнение системы содержит 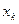 с коэффициентом единица, а во всех остальных уравнениях системы неизвестное
с коэффициентом единица, а во всех остальных уравнениях системы неизвестное 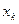 не содержится, т.е. содержится с коэффициентом нуль.
не содержится, т.е. содержится с коэффициентом нуль.
|
|
|
Система уравнений называется разрешенной, если каждое ее уравнение содержит разрешенное неизвестное. Например, система уравнений:
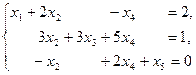
является разрешенной, так как неизвестные 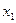 ,
, 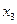 и
и 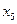 – разрешенные.
– разрешенные.
Если из каждого уравнения разрешенной системы уравнений выбрать по одному разрешенному неизвестному, то получим набор разрешенных неизвестных. Все остальные неизвестные будут называться свободными. В данной системе уравнений  и
и 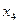 – свободные неизвестные.
– свободные неизвестные.
Общим решением совместной системы уравнений называется равносильная ей разрешенная система, в которой разрешенные неизвестные выражены через свободные. Если в общем решении свободным неизвестным придать какие-нибудь числовые значения, то получим решение данной системы, называемое частным.
Общее решение системы уравнений можно получить с помощью формул Крамера или методом Гаусса.
Пример 3.4. Исследоватьнасовместность,найти общее решение и одно частное решение системы уравнений с помощью формул Крамера:
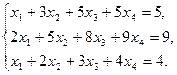
Решение.
1.Запишем расширенную матрицу, найдем ее ранг и одновременно ранг матрицы системы уравнений:
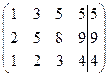 ~
~ 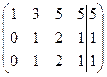 ~
~ 
Таким образом, ранги матриц совпадают и равны 2. Следовательно, система уравнений является совместной.
2.Выберем минор 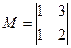 , составленный из коэффициентов, стоящих перед неизвестными
, составленный из коэффициентов, стоящих перед неизвестными 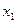 и
и  первого и третьего уравнений. Этот минор отличен от нуля и его порядок равен рангу матрицы системы.
первого и третьего уравнений. Этот минор отличен от нуля и его порядок равен рангу матрицы системы.
3.Выпишем первое и третье уравнения данной системы, содержащие строки минора M:
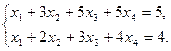

В этих уравнениях оставим в левой части неизвестные 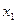 и
и  , а остальные неизвестные перенесем в правую часть:
, а остальные неизвестные перенесем в правую часть:
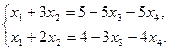

4.Решим полученную систему уравнений по формулам Крамера:

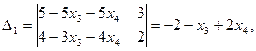
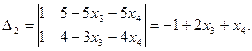
Запишем общее решение данной системы уравнений: 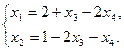 Если свободные неизвестные положить
Если свободные неизвестные положить 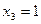 ,
, 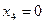 , то из общего решения находим
, то из общего решения находим  ,
, 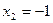 . Следовательно,
. Следовательно, 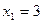 ,
, 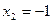 ,
, 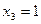 ,
, 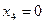 – частное решение исходной системы уравнений.
– частное решение исходной системы уравнений.
Пример 3.5. Найти с помощью метода Гаусса общее решение и одно частное решение системы уравнений:
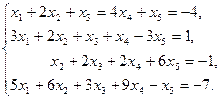
Решение. Запишем систему уравнений в виде таблицы:
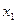
| 
| 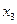
| 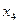
| 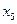
| 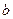
|
| 1 | 2 | 1 | 4 | 1 | -4 |
| 3 | 2 | 1 | 1 | -3 | 1 |
| 0 | 1 | 2 | 2 | 6 | -1 |
| 5 | 6 | 3 | 9 | -1 | -7 |
1.Данная система не содержит противоречивых и тривиальных уравнений. Первое уравнение не содержит разрешенного неизвестного. Неизвестное 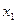 входит в это уравнение с коэффициентом единица. С помощью элементарных преобразований исключим из других уравнений
входит в это уравнение с коэффициентом единица. С помощью элементарных преобразований исключим из других уравнений 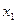 и получим следующую систему уравнений:
и получим следующую систему уравнений:
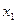
| 
| 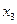
| 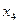
| 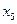
| 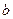
|
| 1 | 2 | 1 | 4 | 1 | -4 |
| 0 | -4 | -2 | -11 | -6 | 13 |
| 0 | 1 | 2 | 2 | 6 | -1 |
| 0 | -4 | -2 | -11 | -6 | 13 |
2.Полученная система не содержит противоречивых и тривиальных уравнений. Третье уравнение содержит неизвестное  с коэффициентом единица. Исключим неизвестное
с коэффициентом единица. Исключим неизвестное  из остальных уравнений с помощью элементарных преобразований:
из остальных уравнений с помощью элементарных преобразований:
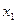
| 
| 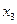
| 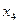
| 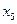
| 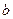
|
| 1 | 0 | -3 | 0 | -11 | -2 |
| 0 | 0 | 6 | -3 | 18 | 9 |
| 0 | 1 | 2 | 2 | 6 | -1 |
| 0 | 0 | 6 | -3 | 18 | 9 |
3.Данная система уравнений не содержит противоречивых и тривиальных уравнений. Она не является разрешенной, так как второе уравнение не содержит разрешенного неизвестного. Разделим это уравнение на -3:
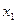
| 
| 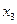
| 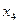
| 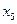
| 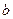
|
| 1 | 0 | -3 | 0 | -11 | -2 |
| 0 | 0 | -2 | 1 | -6 | -3 |
| 0 | 1 | 2 | 2 | 6 | -1 |
| 0 | 0 | 6 | -3 | 18 | 9 |
С помощью элементарных преобразований исключим неизвестное 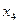 из третьего и четвертого уравнений:
из третьего и четвертого уравнений:
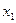
| 
| 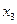
| 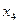
| 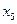
| 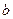
|
| 1 | 0 | -3 | 0 | -11 | -2 |
| 0 | 0 | -2 | 1 | -6 | -3 |
| 0 | 1 | 6 | 0 | 18 | 5 |
| 0 | 0 | 0 | 0 | 0 | 0 |
Запишем полученную разрешенную систему:

в которой 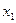 ,
,  ,
, 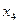 –разрешенные неизвестные, а
–разрешенные неизвестные, а 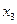 ,
, 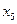 – свободные неизвестные. Общее решение исходной системы уравнений имеет вид:
– свободные неизвестные. Общее решение исходной системы уравнений имеет вид:
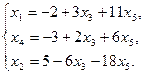
Если положить 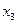 =
= 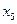 =0, то частное решение исходной системы будет выглядеть следующим образом:
=0, то частное решение исходной системы будет выглядеть следующим образом: 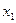 = - 2;
= - 2;  = 5;
= 5; 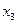 = 0;
= 0; 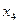 = -3;
= -3; 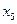 = 0.
= 0.
Задания для самостоятельного решения:
Решить следующие системы уравнений:
3.1.  3.2.
3.2. 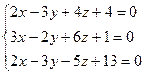 3.3.
3.3. 
3.4. 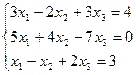 3.5.
3.5. 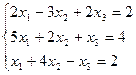 3.6.
3.6. 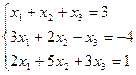
3.7.  3.8.
3.8. 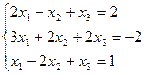 3.9.
3.9. 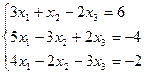
3.10. 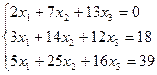 3.11.
3.11. 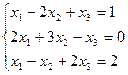 3.12.
3.12. 
3.13. 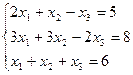 3.14.
3.14. 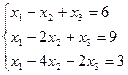 3.15.
3.15. 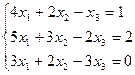
3.16. 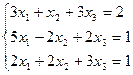 3.17.
3.17. 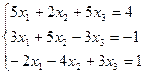 3.18.
3.18. 
3.19. 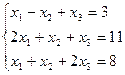 3.20.
3.20. 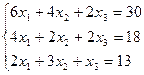 3.21.
3.21. 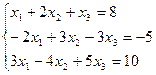
3.22. 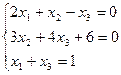 3.23.
3.23.  3.24.
3.24. 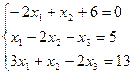
3.25. 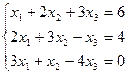 3.26.
3.26. 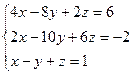 3.27.
3.27. 
3.28. 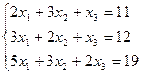 3.29.
3.29. 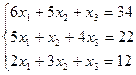 3.30.
3.30. 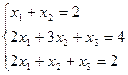
3.31.  3.32.
3.32. 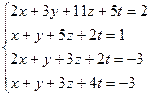 3.33.
3.33. 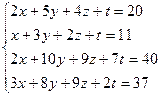
3.34. 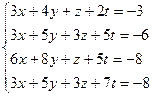 3.35.
3.35. 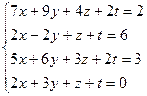 3.36.
3.36. 
3.37. 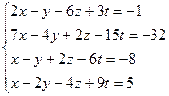 3.38.
3.38.  3.39.
3.39. 
3.40. 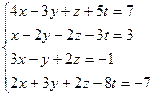 3.41.
3.41. 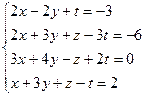 3.42.
3.42. 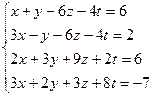
3.43. 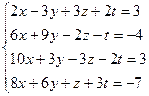 3.44.
3.44. 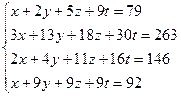 3.45.
3.45. 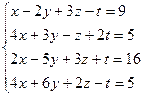
3.46. 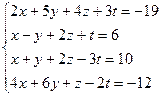 3.47.
3.47. 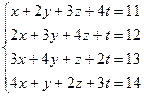
Дата добавления: 2020-12-22; просмотров: 72; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
