Функции, вычислимые алгоритмом
Алгоритм не определяется формально, а существует как бы в виде «всем понятной механической процедуры».
Любая функция, вычислимая на интуитивном (содержательном) уровне, должна быть сконструирована из базовых
Вычислимые функции
Говорят, что машина Тьюринга вычисляет функцию f(x1, x2, ..., xn), если выполняются следующие условия:
1) для любых x1, x2, ..., xn, принадлежащих области определения функции, машина Тьюринга из начальной конфигурации, имея на ленте представление аргументов, переходит в заключительную конфигурацию, имея на ленте результат (представление функции);
2) для любых x1, x2, ..., xn, не принадлежащих области определения функции, машина Тьюринга из начальной конфигурации работает бесконечно.
Если начальная и заключительная конфигурации машины Тьюринга являются стандартными,
то говорят, что машина Тьюринга правильно вычисляет функцию f.
Функция называется вычислимой по Тьюрингу, если существует машина Тьюринга, вычисляющая ее.
Абстрактные универсальные порождающие модели (пример: грамматики).
Алфавит - это непустое конечное множество. Элементы алфавита называютсясимволами.
Цепочка над алфавитом Σ={а1, а2, …, аn} есть конечная последовательность элементоваi.
Множество всех цепочек над алфавитом Σ обозначается Σ*.
Длина цепочки х равна числу ее элементов и обозначается |x|. Цепочка нулевой длиныназывается пустой и обозначается символом ε. Соответственно, непустая цепочка определяется как цепочка ненулевой длины. Пусть имеется алфавит Σ={а, b}. Тогда множество всех цепочек определяется следующим образом: Σ*={ ε, а, b, aa, ab, ba, bb, aaa,aab, aba, . . .}.
|
|
|
Цепочки x и y равны, если они одинаковой длины и совпадают с точностью до порядкасимволов, из которых они состоят.
Над цепочками x и y определена операция сцепления (конкатенации, произведения),которая получается дописыванием символов цепочки y за символами цепочки x.
Язык L над алфавитом Σ представляет собой множество цепочек над Σ. Необходиморазличать пустой язык L=0 и язык, содержащий только пустую цепочку: L={ε}≠0.
Формальный язык L над алфавитом Σ - это язык, выделенный с помощью конечногомножества некоторых формальных правил.
Пусть M и L - языки над алфавитами. Тогда конкатенация LM = {xyx ∈L, y ∈M}. Вчастности, {ε}L = L{ε}=L. Используя понятие произведения, определим итерацию L* и усеченную итерацию L+ множества L:
∞
L+ = UL , i
i =1
∞
L* = UL , i
i =1
где i - степень языка, L определяется рекурсивно следующим образом:
L0 = {ε };
L1 = L;
Ln+1 = Ln L = L Ln;
{ε }L=L{ε }=L.
Например , еслизаданязык L={a}, тогда L*={ε , а , аа , ааа , …}, L+={a, aa, aaa, …}.
|
|
|
Порождающая грамматика - это упорядоченная четверка G= (VT, VN, P, S), где
VT - конечный алфавит, определяющий множество терминальных символов;
VN - конечный алфавит, определяющий множество нетерминальных символов;
Р - конечное множество правил вывода, т.е. множество пар следующего вида:
u → v, где u, v ∈(VT ∪VN)*;
S - начальный символ (аксиома грамматики), S ∈VN.
Из терминальных символов состоят цепочки языка, порожденного грамматикой. Аксиомой называется символ в левой части первого правила вывода грамматики.
Для того чтобы различать терминальные и нетерминальные символы, принятообозначать терминальные символы строчными, а нетерминальные символы заглавными буквами латинского алфавита.
В грамматике G цепочка х непосредственно порождает цепочку у, если х = αuβ, у = αvβ
и u→v ∈Р, т.е. цепочка у непосредственно выводится из х, что обозначается х => у.
Языком, порождаемым грамматикой G = (VT, VN, Р, S), называется множество терминальных цепочек, выводимых в грамматике G из аксиомы:
L(G) = {х | х ∈ VT*; S => *х}, где =>*- выводимость.
Пример. Дана грамматика G = (VT, VN, Р, S), в которой VT = {а, b}, VN = {S}, Р = {S →aSb, S → ab). Определить язык, порождаемый этой грамматикой.
|
|
|
Решение. Используя рекурсию, выведем несколько цепочек языка, порождаемого данной грамматикой:
S → ab;
S → aSb =>aabb;
S → aSb =>aaSbb =>aaabbb; . . .
Определим язык, порожденный данной грамматикой:
L(G) = {anbn | n > 0}.
Говоря о представлении грамматик, нужно отметить, что множество правил вывода грамматики может приводиться без специального указания множеств терминалов и нетерминалов. В таком случае обычно предполагается, что грамматика содержит в точности те терминальные и нетерминальные символы, которые встречаются в правилах вывода.
Также предполагается, что правые части правил, для которых совпадают левые части,можно записать в одну строку с использованием разделителя. Так, правила вывода из приведенного примера можно записать следующим образом: S → aSb | ab.
Сложность вычисления
Скорость выполнения программы (или производительность) зависят от многих факторов: языка программирования, способа реализации транслятора (компилятор или интерпретатор), производительности процессора.
Поэтому заранее оценить производительность еще не написанной программы сложно.
|
|
|
Вместе с тем, достаточно часто требуется оценить перспективы использования алгоритма с различными объемами данных. Для этого вводится понятие трудоемкости.
Трудоемкость программы (алгоритма) — зависимость количества массовых операций (сравнения, обмены, повторения циклов) от объема (размерностей) обрабатываемых данных.
Рассмотрим алгоритмы вычисления значения многочлена степени n в заданной точке x.

Алгоритм 1.
Для каждого слагаемого, кроме свободного члена, возводим x в нужную степень последовательным умножением и домножаем результат на коэффициент. После находим сумму.
Умножений всего
Сложений всего
Всего операций
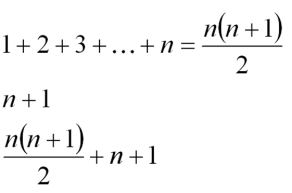
Алгоритм 2.
Представим многочлен в виде

n раз последовательно выполняются операции умножения и сложения.
Всего 2n операций.
Чаще всего такая подробная оценка не требуется. Вместо нее приводят лишь асимптотическую скорость возрастания числа операций при увеличении n.
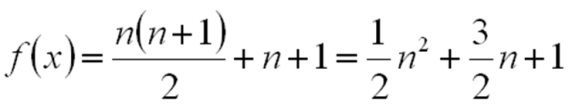
Функция квадратичная, медленно растущей линейной частью можно пренебречь. Асимптотическаяоценка обозначается O(n2).Читается «О большое от эн квадрат».
Наилучшей оценкой является О(1). В этом случае время работы вообще не зависит от n. Например, сумму чисел 1+2+3+…+n можно найти без использования цикла по формуле суммы членов арифметической прогрессии.
Если программа устроена так, что происходит постоянное удвоение некоторого значения (или деление его пополам), то число операций L связано с размерностью данных n формулой 2L=n. Оценка трудоемкости обозначается O(log n).
Если решение задачи состоит из m шагов, каждый из которых порождает аналогичную задачу (например, рекурсивное определение числа Фибоначчи), то трудоемкость растет «лавинообразно» и говорят об экспоненциальном росте трудоемкости, обозначается O(2n).
Это самый плохой случай, самая неэффективная программа.
Правила формирования оценки О()
1. При оценке О() берем количество операций, растущее быстрее всего. При сортировке выбором ищем максимальный элемент в неупорядоченной части и меняем его с последним элементом в этой части. Число сравнений имеет оценку О(n2), число обменов — О(n).
2. При оценке О() константы не учитываются. Пусть один алгоритм делает 1000n+500 операций, а другой — 10n+2 операции. Оба алгоритма имеют оценку O(n), так как их время работы растет линейно. Алгоритмы с одинаковой оценкой О() могут быть не одинаково эффективны
При рассмотрении сложности алгоритма нельзя обращать внимание только на быстродействие (временную сложность алгоритма), должно учитывать необходимую для работы программы память (пространственную сложность алгоритма).
Как правило, ускорение алгоритма возможно за счет выделения дополнительной памяти и наоборот
Дата добавления: 2020-12-22; просмотров: 272; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
