Определение тесноты связи между случайными величинами
Лекции на 04.12.2020 г. и 11.12.2020 г.
Анализ результатов эксперимента
Характеристика видов связей между рядами наблюдений
На практике большинство измерений связаны с установлением зависимости одних величин от изменения других. В таком случае целью эксперимента является получение функциональной зависимости 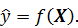 Для этого должны одновременно определяться значения
Для этого должны одновременно определяться значения 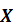 и соответствующие им значения
и соответствующие им значения 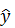 , а задачей эксперимента является построение математической модели исследуемой зависимости. Другими словами, речь идет об установлении связи между двумя рядами наблюдений.
, а задачей эксперимента является построение математической модели исследуемой зависимости. Другими словами, речь идет об установлении связи между двумя рядами наблюдений.
Из всего многообразия связей обычно выделяют следующие два вида: функциональные связи (или зависимости) – при изменении одной величины 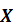 другая
другая 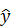 изменяется так, что каждому значению
изменяется так, что каждому значению 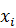 соответствует совершенно определенное (однозначное) значение yi
соответствует совершенно определенное (однозначное) значение yi
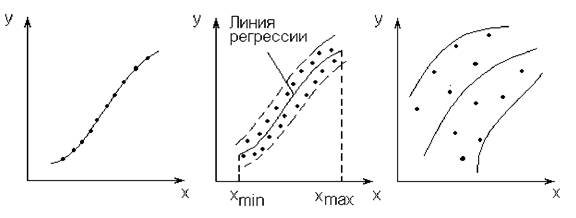
А) б) в)
Рисунок 6.1 - Функциональная и стохастическая связь
Однако, на практике такой вид связей встречается достаточно редко. Влияние отдельных случайных факторов может быть достаточно мало, но в совокупности они могут существенно влиять на результаты эксперимента. В этом случае отмечаем наличие стохастической (вероятностной) связи между переменными.
Стохастические связи характеризуются тем, что переменная y реагирует на изменение другой переменной (переменных) Х изменением своего закона распределения. В результате зависимая переменная принимает не одно конкретное значение, а несколько из возможного множества значений; повторяя испытания, будем получать другие значения функции отклика, и одному значению х в различных реализациях будут соответствовать различные значения у.
|
|
|
На рис.6.1. б) – кривая зависимости, проходящая по центру полосы экспериментальных точек (математическому ожиданию), которые могут и не лежать на искомой кривой y = f ( X ), и занимают некоторую полосу вокруг нее. Эти отклонения вызваны погрешностями измерений, неполнотой модели и учитываемых факторов, случайным характером самих исследуемых процессов и т.п.
Анализ стохастических связей приводит к различным постановкам задач статистического исследования зависимостей, которые упрощенно можно классифицировать следующим образом:
1) Задачи корреляционного анализа – исследование наличия взаимосвязей между отдельными группами переменных;
2) Задачи регрессионного анализа – задачи, связанные с установлением аналитических зависимостей между переменным у и одним или несколькими переменными х1,х2,…,хк , которые носят количественный характер;
|
|
|
3) Задачи дисперсионного анализа – задачи, в которых переменные х1,х2,…,хк носят качественный характер, а исследуется и устанавливается степень их влияния на у.
Стохастические зависимости характеризуются формой, теснотой связи, численными значениями коэффициентов уравнения регрессии.
Форма связи устанавливает вид функциональной зависимости 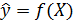 и характеризуется уравнением регрессии. Если уравнение связи линейное, имеем линейную многомерную зависимость:
и характеризуется уравнением регрессии. Если уравнение связи линейное, имеем линейную многомерную зависимость:
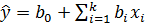 (6.1)
(6.1)
где в0,в1,…,вк – коэффициенты уравнения.
Следует отметить, что задача выбора функциональной зависимости – неформальная. Решение о выборе той или иной математической модели остается за исследователем. Только экспериментатор знает, для какой цели создается, и как в дальнейшем будет использоваться создаваемая модель.
В наш компьютерный век построение модели не является сложной задачей, если исследователь четко представляет цель и задачи исследования. Поэтому для уяснения сущности и упрощения выкладок остановимся на рассмотрении сущности метода наименьших квадратов.
Метод наименьших квадратов
Данный метод определения неизвестных коэффициентов уравнения регрессии был разработан Лежандром и Гауссом почти 200 лет назад.
|
|
|
Определение коэффициентов bj методом наименьших квадратов основано на выполнении требования, чтобы сумма квадратов отклонений экспериментальных точек от соответствующих значений уравнения регрессии была минимальна. Математическая запись этого требования выглядит следующим образом:
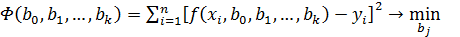
где n - число экспериментальных точек в рассматриваемом интервале изменения аргумента.
Необходимым условием минимума функции 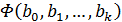 является выполнение равенства
является выполнение равенства
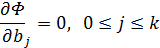
или
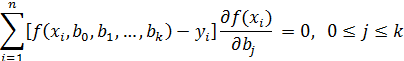
После преобразования получим
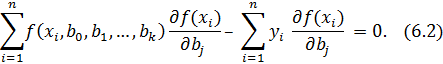
Система уравнений (6.2) содержит столько же уравнений, сколько неизвестных коэффициентов 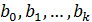 , входит в уравнение регрессии, и называется в математической статистике системой нормальных уравнений.
, входит в уравнение регрессии, и называется в математической статистике системой нормальных уравнений.
Поскольку 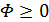 при любых
при любых 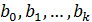 величина
величина 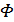 обязательно должна иметь хотя бы один минимум. Поэтому, если система нормальных уравнений имеет единственное решение, оно и является минимумом для этой величины.
обязательно должна иметь хотя бы один минимум. Поэтому, если система нормальных уравнений имеет единственное решение, оно и является минимумом для этой величины.
Расчет регрессионных коэффициентов методом наименьших квадратов можно применять при любых статистических данных, распределенных по любому закону.
Определение тесноты связи между случайными величинами
Определив уравнение теоретической линии регрессии, необходимо дать количественную оценку тесноты связи между двумя рядами наблюдений. Линии регрессии, изображенные на рис. 6.1.б,в, одинаковы, но точки на рис. 6.1,б значительно ближе расположены к кривой, чем на рис. 6.1.в.
|
|
|
При корреляционном анализе предполагается, что факторы и отклики носят случайный характер и подчиняются нормальному закону распределения.
Теснота связи между случайными величинами характеризуется корреляционным отношением 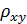 . Рассмотрим физический смысл этого показателя, для чего необходимо ввести некоторые понятия (рис. 6.2).
. Рассмотрим физический смысл этого показателя, для чего необходимо ввести некоторые понятия (рис. 6.2).
Остаточная дисперсия (остатки) 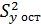 - характеризует разброс экспериментально наблюдаемых точек относительно линии регрессии и представляет собой показатель ошибки предсказания параметра у по уравнению регрессии:
- характеризует разброс экспериментально наблюдаемых точек относительно линии регрессии и представляет собой показатель ошибки предсказания параметра у по уравнению регрессии:
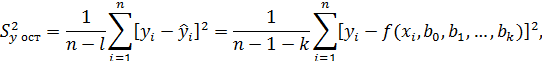
где 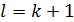 - число коэффициентов уравнения модели.
- число коэффициентов уравнения модели.
Общая дисперсия (общий) 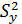 -характеризует разброс экспериментального материала относительно среднего значения, т.е. линии С (рис. 6.2)
-характеризует разброс экспериментального материала относительно среднего значения, т.е. линии С (рис. 6.2)
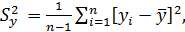
где 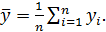
Средний квадрат отклонения линии регрессии от среднего значения линии С (средний) :
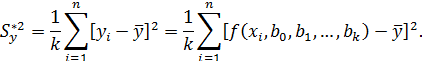
Очевидно, что общая дисперсия 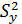 (сумма квадратов относительно среднего значения) равна остаточной дисперсии
(сумма квадратов относительно среднего значения) равна остаточной дисперсии 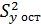 (сумма квадратов относительно линии регрессии) плюс средний квадрат отклонения линии регрессии
(сумма квадратов относительно линии регрессии) плюс средний квадрат отклонения линии регрессии 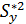 (сумма квадратов, обусловленная регрессией).
(сумма квадратов, обусловленная регрессией).
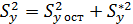
Разброс экспериментально наблюдаемых точек относительно линии регрессии характеризуется безразмерной величиной – выборочным корреляционным отношением, которое определяет долю, которую привносит величина Х в общую изменчивость случайной величины у.
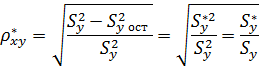
Проанализируем свойства этого показателя.
1. В том случае, когда связь является не стохастической, а функциональной, корреляционное отношение равно 1, так как все точки корреляционного поля оказываются на линии регрессии, остаточная дисперсия равна 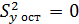 , а
, а 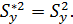
2. Равенство нулю корреляционного отношения указывает на отсутствие какой-либо тесноты связи между величинами х и у для данного уравнения регрессии, поскольку разброс экспериментальных точек относительно среднего значения и линии регрессии одинаков, т.е. 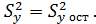
3. Чем ближе расположены экспериментальные данные к линии регрессии, тем теснее связь, тем меньше остаточная дисперсия и тем больше корреляционное отношение.
Следовательно, корреляционное отношение может изменяться в пределах от 0 до 1.
Для рассмотрения сути изучаемого вопроса нами был рассмотрен простейший случай статистической обработки, методология решения более сложных задач принципиально не отличается.
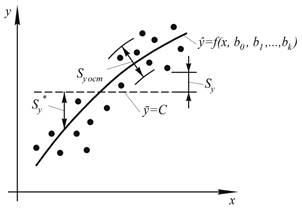
Рисунок 6.2 – Иллюстрация основных характеристик корреляционного анализа
Регрессионный анализ
Как и корреляционный анализ, регрессионный включает в себя построение уравнения регрессии (например, методом наименьших квадратов) и статистическую оценку результатов.
При проведении регрессионного анализа принимаются следующие допущения:
1. Входной параметр х изменяется с весьма малой ошибкой. Появление ошибки в определении у объясняется наличием в процессе не выявленных переменных и случайных воздействий, не вошедших в уравнение регрессии.
2. Результаты наблюдений выходной величины – независимые нормально распределенные случайные величины.
3. При проведении параллельных опытов выборочные дисперсии должны быть однородны. При выполнении измерений в различных условиях возникает задача сравнения точности измерений, а это возможно осуществлять при наличии однородных дисперсий (т.е. принадлежности экспериментальных данных к одной генеральной совокупности).
После того, как уравнение регрессии найдено, необходимо провести статистический анализ результатов. Этот анализ состоит в установлении адекватности уравнения и проверке значимости коэффициентов уравнения.
Проверка адекватности модели
Регрессионная модель называется адекватной, если предсказываемые по ней значения у согласуются с результатами наблюдений. Так, построив линейную модель, мы хотим убедиться, что никакая другая модель не даст значительного улучшения в описании предсказания значений у. В основе процедуры проверки адекватности модели лежат предположения, что случайные ошибки наблюдений являются независимыми, нормально распределенными случайными величинами с нулевыми средними значениями и одинаковыми дисперсиями.
Сформулируем нуль-гипотезу Н0: «Уравнение регрессии адекватно».
Альтернативная гипотеза Н1: «Уравнение регрессии неадекватно».
Для проверки этих гипотез принято использовать F-критерий Фишера. При этом общую дисперсию (дисперсию выходного параметра) 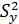 сравнивают с остаточной дисперсией
сравнивают с остаточной дисперсией 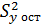 . Определяется экспериментальное значение F - критерия:
. Определяется экспериментальное значение F - критерия:
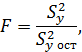
который в данном случае показывает, во сколько раз уравнение регрессии предсказывает результаты опытов лучше, чем среднее 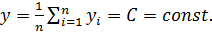 Если
Если 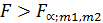 то уравнение регрессии адекватно. Чем больше значение
то уравнение регрессии адекватно. Чем больше значение 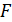 превышает
превышает 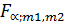 для выбранного α и числа степеней свободы
для выбранного α и числа степеней свободы 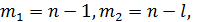 тем эффективнее уравнение регрессии.
тем эффективнее уравнение регрессии.
Рассмотрим случай, когда для повышения надежности и достоверности осуществляется не одно, а m параллельных опытов (примем, что это число одинаковым для каждого фактора). Тогда общее число экспериментальных значений величины у составит N = n * m.
В этом случае оценка адекватности модели производится следующим образом:
1. определяется среднее из серии параллельных опытов: 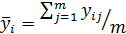
2. рассчитываются значения параметра 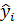 по уравнению регрессии
по уравнению регрессии
3. рассчитывается дисперсия адекватности: 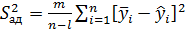
4. определяются выборочные дисперсии для параллельных опытов 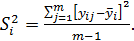
5. Определяется дисперсия воспроизводимости 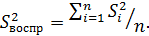 Число степеней свободы этой дисперсии равно
Число степеней свободы этой дисперсии равно 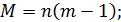
6. Определяется экспериментальное значение критерия Фишера: 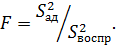
7. Определяется теоретическое значение критерия Фишера 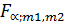 , где
, где 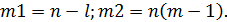
8. Если 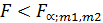 , то уравнение регрессии адекватно, в противном случае – нет.
, то уравнение регрессии адекватно, в противном случае – нет.
Дата добавления: 2020-12-22; просмотров: 236; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
