Однородные тригонометрические уравнения.
Изучение нового материала.
Сегодня мы изучим с вами
- квадратные уравнения относительно 
или. 
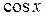(явного вида, пример 1-а), или сводящиеся к явному виду после использования основного тригонометрического тождества – это пример 1-б)) При их решении будим использовать метод замены переменной и метод разложения на множители;
- уравнения специального вида: однородные уравнения первой степени, однородные уравнения второй степени.
1.Метод замены переменной
ПРИМЕР 1-а)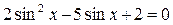 
Решение: Введём новую переменную: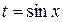 
. Тогда уравнение примет вид: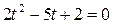 
D=25-16=9,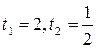 
. Значит, либо 
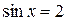, либо 
Первое из этих уравнений не имеет решений, а для второго получаем: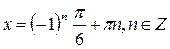 
Ответ: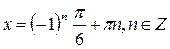
ПРИМЕР 1-б) 
Решение: Если в уравнение входят тригонометрические функции, то их, если возможно, надо выразить через одну. При этом следует выбрать эту функцию так, чтобы получилось квадратное относительно неё уравнение. Воспользуемся тем, что 
. Тогда заданное уравнение можно переписать в виде:
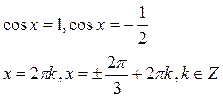
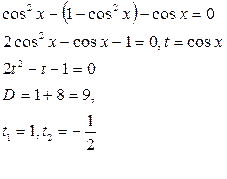
Ответ: 
2. Метод разложения на множители.
Т.е. если уравнение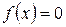 
удаётся преобразовать к виду 
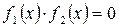, то либо 
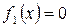, либо 
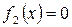. В подобных случаях обычно говорят так: задача сводится к решению совокупности уравнений 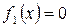; 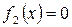. При решении тригонометрических уравнений, решаемых разложением на множители, нужно использовать все известные способы разложения на множители: вынесения общего множителя за скобки; группировка; применение формул сокращённого умножения и деления, искусственные приёмы.
|
|
|
ПРИМЕР 2-а)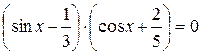 
Решение: Задача сводится к решению совокупности уравнений: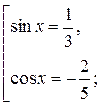 
Из этих уравнений находим соответственно: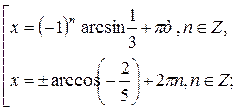 
Ответ: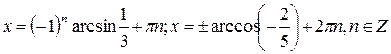 
Вернёмся к уравнению 1-б). Мы свели его к совокупности уравнений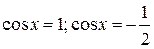 
и записали ответ в виде:
Далее, мы рассмотрели уравнение 2-а), свели его к совокупности уравнений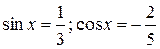 
и записали ответ в виде: 
В обоих случаях в качестве параметра использовалась одна и та же буква (в первом примере – k, во втором – n).И это правильно. Но если бы мы записали ответы в виде, соответственно:
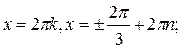
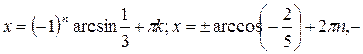то это тоже было бы верным. Здесь речь идёт о совокупности уравнений, т.е. о независимых друг от друга уравнениях. А вот в системах тригонометрических уравнений дело обстоит иначе: там необходимо использовать разные обозначения для параметра в различных уравнениях системы, это носит принципиальный характер.
ПРИМЕР 2-б) 
Решение: Имеем: 
. Значит приходим к совокупности уравнений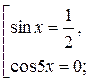 
.
Из первого уравнения находим: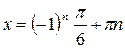 
.
Из второго уравнения находим: 
.
Ответ: ,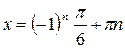 
Внимание! Переход от уравнения 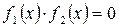к совокупности уравнений 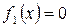, 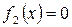не всегда безопасен.
ПРИМЕР 2-в)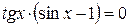 
Из уравнения 
находим: 
; из уравнения 
находим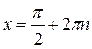 
.
Но включить обе серии решений в ответ нельзя. Дело в том, что при значениях 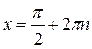входящий в заданное уравнение множитель 
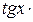не имеет смысла, т.е. значения 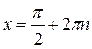не принадлежат области определения уравнения (ОДЗ) – это посторонний корень.
|
|
|
Ответ: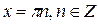 
Однородные тригонометрические уравнения.
Определение: Уравнение вида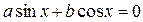 
называют однородным тригонометрическим уравнением первой степени относительно 
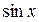и 
. В результате получается уравнение вида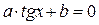 
.
Определение: Уравнение вида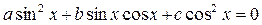 
называется однородным тригонометрическим уравнением второй степени относительно 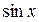и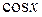 
.
Если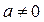 
, то разделим обе части уравнения на 
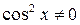, получаем уравнение 
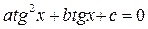; если 
, то уравнение принимает вид 
и решается разложением на множители левой части: 
.
1. Сначала поговорим о решении однородных тригонометрических уравнений первой степени.
Дано уравнени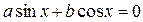е , где ,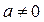 
. Разделив обе части уравнения почленно на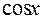 
, получим: 
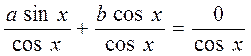; т.е. 
.
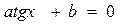В итоге приходим к простейшему тригонометрическому уравнению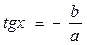 
Внимание! Делить обе части уравнения на одно и то же выражение можно только в том случае, когда мы уверены, что это выражение нигде не обращается в нуль (на 0 делить нельзя). Уверены ли мы, что в рассматриваемом случае 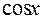отличен от нуля? Предположим, что 
. Тогда однородное уравнение 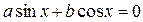примет вид 
, т.е.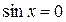 
(вы ведь не забыли, что коэффициент 
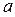отличен от нуля). Получается, что и , и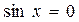 
, а это не возможно, т.к. 
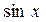и 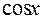обращаются в нуль в различных точках.
|
|
|
Уравнения вида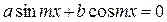 
тоже называют однородными тригонометрическими уравнениями первой степени. Для их решения обе части уравнения почленно делят на 
.
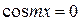ПРИМЕР 3.1-а)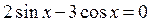 
Решение: Разделим обе части уравнения на 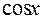, получим:
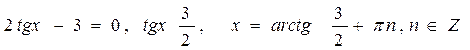
Ответ: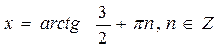 
.
ПРИМЕР 3.1-б)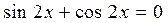 
Решение: Разделим обе части уравнения почленно на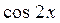 
, получим:
Ответ: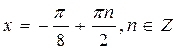 
2. Рассмотрим теперь однородные тригонометрические уравнения второй степени.
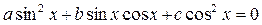
Если коэффициент 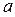отличен от нуля, т.е. в уравнении содержится член 
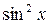с каким-то коэффициентом, отличным от нуля, то, рассуждая как и выше, легко убедится в том, что при интересующих нас значениях переменной 
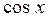не обращается в нуль, а потому можно обе части уравнения разделить почленно на 
:
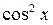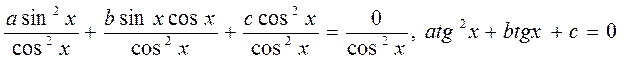
Это квадратное уравнение относительно новой переменной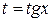 
.
Пусть теперь в однородном тригонометрическом уравнении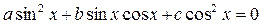 
коэффициент , т.е. отсутствует член 
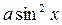. Тогда уравнение принимает вид
. Это уравнение можно решить методом разложения на множители:
, или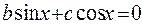 
Получились два уравнения, которые мы решать умеем.
|
|
|
Аналогично обстоит дело и в случае, когда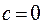 
, т.е. когда однородное уравнение имеет вид 
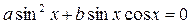(здесь можно вынести за скобки 
).
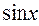Фактически мы выработали
Алгоритм решения уравнения
|
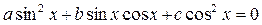
Так же обстоит дело и в однородных уравнениях вида 
ПРИМЕР 3.2-а)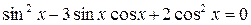 
.
Решение: Разделим обе части уравнения почленно на 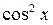, получим:
Значит, либо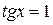 
, либо 
Из первого уравнения находим: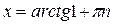 
, т.е. 
.
Из второго уравнения находим: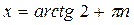 
. Ответ: ; 
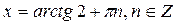
ПРИМЕР 3.2-б) 
Решение: Здесь отсутствует член вида 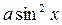, значит, делить обе части уравнения на 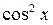нельзя. Решим уравнение методом разложения на множители:
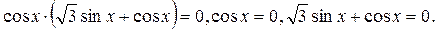Из первого уравнения находим: 
. Второе уравнение – однородное тригонометрическое уравнение первой степени. Решим его с помощью почленного деления обеих частей уравнения на :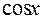
Ответ: , 
.
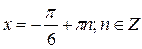Дата добавления: 2020-12-22; просмотров: 91; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!