Основные теоремы о пределах. Стр 118
Лекция №3
Тема : Предел функции в точке. Раскрытие неопределенности.
Предел числовой последовательности
Числовой последовательностью называется бесконечное множество чисел, имеющих определенные номера. Эти числа являются членами последовательности.
Последовательность обозначается: { уn }или yn или у1, у2, у3, …, уn, … где n=1, 2,… .
Число называется пределом последовательности , если, начиная с некоторого места, все члены этой последовательности будут сколь угодно мало отличаться от данного числа.
Пример: уn = 
1;  ;
;  ; …….
; …….  ; ………
; ………

чем больше номер члена последовательности, тем меньше этот член отличается от числа 0
Обозначение 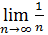 = 0
= 0
Определение: Число b Є R называется пределом последовательности {у n }, если по мере возрастания номера n , n -й член у n неограниченно приближается к b .
Обозначение: 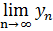 = b или уn
= b или уn 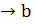 при n
при n 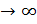
Говорят, что последовательность {у n } сходится к b .
Понятие предела имеет и более строгое определение:
Постоянное число а называется пределом последовательности {xn}, если для любого сколь угодно малого положительного числа ε > 0 существует номер N, что все значения xn, у которых n>N, удовлетворяют неравенству |xn - a| < ε.

Определение. Последовательность, имеющая предел , называется сходящейся. Последовательность, не являющаяся сходящейся, называется расходящейся.
|
|
|
(подразумевается, что предел – конечное число).
Функция»
Определение: Если каждому числу х из множества чисел D поставлено в соответствие единственное число у, то говорят, что на множестве D задана функция f и пишут y=f(x), где х - называется независимой переменной или аргументом этой функции,
у, f(x) – зависимой переменной или функцией,
а множество D - областью определения этой функции.
Все значения, которые принимает функция f(x) (при х 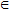 D), образуют область значения функции Е.
D), образуют область значения функции Е.
Существует три способа задания функции: табличный, аналитический (с помощью формулы у=f(х), где f(x) некоторое выражение с переменной х ), графический.
Пример. Функция у=f(х) задана аналитической формулой:
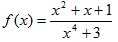
Найти f(0)
Чтобы найти f(0), надо в f(х) всюду вместо х подставить 0. Получим:
f (0) = 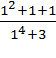 =
= 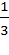
Определение: Сложная функция – композиция нескольких функций.
Функцию y=f(φ(x)) называют композицией двух функций y=f(u) и u=φ(x).
Сложная функция может быть композицией большего числа функций: трех, четырех и т.д. Например, функция y=cos(x2+1) - композиция двух функций y=cosu и u=x2+1; функция y=lg(sin2x) - композиция трех функций.
|
|
|
К основным элементарным функциям относятся пять классов функций: степенные, показательные, логарифмические, тригонометрические и обратные тригонометрические.
3. «Предел функции»
Пусть функция f(x) определена в некоторой окрестности точки х = а (т.е. в самой точке х = а функция может быть и не определена)
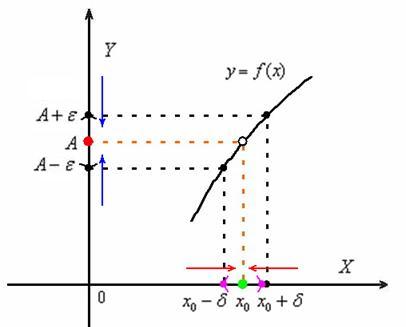
Определение. Число b называется пределом функции f(x) при х 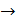 а, если по мере того, как х приближается к а(справа или слева) значение функции неограниченно приближается к b
а, если по мере того, как х приближается к а(справа или слева) значение функции неограниченно приближается к b
Запись предела функции в точке:  = b
= b
Понятие предела функции в точке имеет и более строгое определение:
Пусть дана функция f(x) и пусть a - предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a. Точка a может принадлежать множеству D(f), а может и не принадлежать ему.
Определение 1. Постоянное число А называется пределом функции f(x) при x→ a, если для всякой последовательности {xn} значений аргумента, стремящейся к а, соответствующие им последовательности {f(xn)} имеют один и тот же предел А.
Это определение называют определением предела функции по Гейне, или “на языке последовательностей”.
Определение 2. Постоянное число А называется пределом функции f(x) при x→a, если, задав произвольное, как угодно малое положительное число ε, можно найти такое δ >0 (зависящее от ε), что для всех x, лежащих в δ -окрестности числа а, т.е. для x, удовлетворяющих неравенству | x-a |< δ , значения функции f(x) будут лежать в ε-окрестности числа А, т.е. |f(x)-A| < ε
|
|
|
Это определение называют определением предел функции по Коши, или “на языке ε - δ"
В том случае, если последовательность функций {f(xn)} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а, то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде:
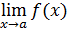 =
= 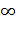 ,
, 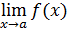 =
=  .
.
Переменная величина (т.е. последовательность или функция), предел которой равен нулю, называется бесконечно малой величиной.
Переменная величина, предел которой равен бесконечности, называется бесконечно большой величиной.
Утверждения:
1)  = 0
= 0
2) 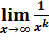 = 0 , где k Є N
= 0 , где k Є N
( т.е. величина обратная бесконечно большой является бесконечно малой)
Чтобы найти предел на практике пользуются следующими теоремами.
Основные теоремы о пределах. Стр 118
Теорема 1.  , где С = const, т.е. предел постоянной величины равен самой постоянной.
, где С = const, т.е. предел постоянной величины равен самой постоянной.
|
|
|
Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х 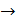 а.
а.
Теорема 2. 
Предел суммы (разности) двух функций равен сумме (разности) пределов этих функций
Теорема 3. 
Предел произведения двух функций равен произведению пределов этих функций
Следствие. 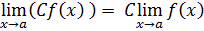
Постоянный коэффициент можно выносить за знак предела
Теорема 4. 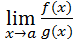 =
= 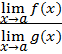 при
при 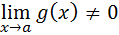
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен
Теорема 5. для непрерывной функции можно переставлять знак предела и знак функции
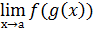 = f(
= f( 
Например, предел степенной функции
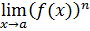 = (
= ( 
Пример 1. 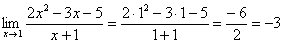
Метод подстановки: нужно просто подставить число к которому стремится переменная х вместо переменной х в функцию, стоящую под знаком предела.
Раскрытие неопределенности.
Пример 2.
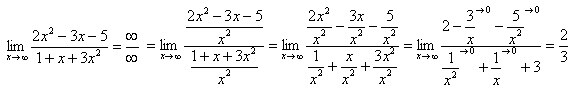
Чтобы раскрыть неопределенность  - надо разделить числитель и знаменатель дроби на наивысшую из имеющихся степень переменной
- надо разделить числитель и знаменатель дроби на наивысшую из имеющихся степень переменной
Пример 3.
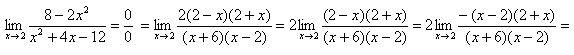
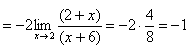
Чтобы раскрыть неопределенность  - надо преобразовать дробь, стоящую при пределе. Например, сократить.
- надо преобразовать дробь, стоящую при пределе. Например, сократить.
Первый замечательный предел.
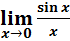 = 1
= 1
Следствие:  = 1 , где С = const
= 1 , где С = const
Док-во: Замена Сх=t.
Т.к. х→0, то Сх→0.
Итак, t→0. 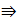
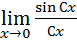 =
= 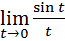 = 1
= 1
Примеры
1. 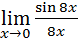 = 1
= 1
2.  =
= 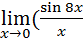
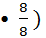 =
=  8
8 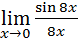 = 8
= 8
3.  =
= 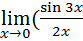 •
•  )=
)= 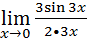 =
= 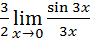 =
= 
Дата добавления: 2020-12-22; просмотров: 159; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
