Индексы цен Пааше, Ласпейреса, Фишера.
Индексы.
Определение индекса и его виды
Индексы (лат. index - показатель, указатель) – относительные показатели, многие из которых обладают спецификой построения, позволяющей складывать несоизмеримые явления при обобщающем сравнении экономических показателей.
Специфика проявляется при построении агрегатных и средних индексов.
Индексная теория широко используется для расчета показателей в макро- и микроэкономике.
Индексируемая величина – признак, изменение которого изучается.
Различают следующие виды индексов:
1. По характеру отношения:
1.1.Динамические индексы - сравнение во времени.
1.2.Территориальные индексы - сравнение в пространстве.
1.3.Индексы сравнения фактических данных с плановыми(договорными, нормативными, прогнозируемыми).
2. По степени охвата единиц совокупности:
2.1. Индивидуальные индексы (i)- соотношение величин, характеризующих простые, соизмеримые явления.
2.2. Сводные индексы (I)- соотношение обобщенных уравновешенных величин, характеризующих сложные явления.
3. В зависимости от содержания индексируемой величины:
3.1. Индексы количественных показателей. Количественный показатель характеризует весь оббьем статистической совокупности.
4. По способу сравнения:
4.1. Базисные индексы, когда база сравнения постоянная.
4.2. Цепные индексы, когда база сравнения переменная.
5. В зависимости от методологии расчета сводных индексов:
|
|
|
5.1 Агрегатные индексы - соотношение двух сумм (агрегатов) произведений значений признаков изучаемой статистической совокупности.
5.2. Средние индексы - средние взвешенные арифметические и гармонические; их строят на базе агрегатных, если нет отчетных или базисных значений индексируемой величины, но известны индивидуальные индексы.
Построение и анализ индивидуальных и агрегатных индексов.
Индивидуальные индексы
1. Индивидуальные индексы физического объема:

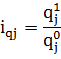
(1)
Где qj – количество j-го вида продукции (товара) в натуральном выражении;
1- отчетные данные;
0- база сравнения (постоянная или переменная).
2. Индивидуальные индексы цен:
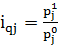 (2)
(2)
где pj- цена j-го вида товара.
3. Индивидуальный индекс объема продаж:
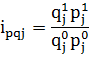
(3)
Аналогично строятся все остальные индивидуальные индексы.
Методику анализа индексов покажем на примере агрегатных индексов.
Агрегатные индексы.
1. Агрегатный индекс объема продаж:
|
|
|
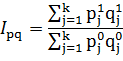
(4)
Построенный индекс позволяет ответить на три вопроса:
- что показывает сам индекс;
- что показывает относительное отклонение, построенное на базе данного индекса;
- что показывает абсолютное отклонение, построенное на базе данного индекса.
Ответим последовательно на эти три вопроса.
1)Агрегатный индекс объема продаж показывает, во сколько раз возрос объем продаж в отчетном периоде по сравнению с базисным ( или сколько процентов составляет рост объема продаж).
Если Ipq>1 (или 100%)- рост объема продаж.
Если Ipq<1 (или 100%)- снижение объема продаж.
Если Ipq=1 (или 100%)- изменений нет.
2) Относительное отклонение, построенное на базе агрегатного индекса объема продаж, показывает, на сколько процентов (долей единицы) увеличился (уменьшился) объем продаж в отчетном периоде по сравнению с базисным.
Если индекс рассчитан в процентах, то:
 (5)
(5)
Если индекс рассчитан в коэффициентах, то:
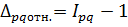
(6)
3) Абсолютное отклонение, построенное на базе агрегатного индекса объема продаж, показывает, на сколько рублей увеличился (уменьшился) объем продаж в отчетном периоде по сравнению с базисным.
|
|
|
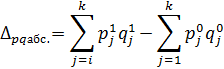
(6)
Абсолютное и относительное отклонения со знаком «+» означают прирост, а со знаком «-»- сокращение.
2. Агрегатный индекс физического объема. Здесь индексируемая величина – количество продукции (товаров), которое может быть совершенно несоизмеримым для разных видов продукции. Невозможно сравнивать килограммы и метры, литры и штуки и т.п.
Для уравновешивания несоизмеримых показателей вводится признак-вес.
Вес индекса- признак, служащий для соизмерения несоизмеримых явлений, который вводится в индекс постоянной фиксированной величиной в качестве сомножителя для индексируемой величины.
Индексируемая величина при этом выступает в качестве признака-фактора, а произведение признака-фактора и признака-веса дает результативный показатель.
В агрегатном индексе физического объема в качестве признака-фактора выступает количество продукции (товара), а в качестве признака-веса берется цена на эту продукцию (товар), что позволяет перейти к соизмеримому показателю- объему продаж (результативный показатель).
При построении индексов, требующих введения признака-веса, возникает вопрос, в качестве базисного или отчетного показателя следует применять вес индекса? Ответить на этот вопрос позволяет следующее правило.
|
|
|
Правило применения весов при построении индексов:
- для количественных индексируемых величин веса следует брать базисные;
- для качественных индексируемых величин веса следует брать отчетные. Это правило основано на первичности построения показателей.
Сначала, например, при планировании производства и реализации продукции появляется показатель «количество продукции» (количественный показатель), а затем – средняя цена единицы продукции (качественный показатель).
В соответствии с указанным правилом в агрегатном индексе физического объема в качестве признака-веса следует брать базисные цены, и тогда индекс физического объема будет иметь следующий вид:
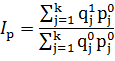
(7)
Построение агрегатных индексов с весами базисного периода первым предложил немецкий экономист Э. Ласпейрес (1864 г.), и с тех пор этот метод носит его имя.
Отметим, что при построении агрегатных индексов индексируемую величину принято писать сразу после знака суммы, а признак-вес- следующим.
Построив агрегатный индекс физического объема, ответим на поставленные ранее традиционные три вопроса.
1) Индекс физического объема показывает, во сколько раз возрос объем продаж в отчетном периоде по сравнению с базисным из-за изменения физического объема (или сколько процентов составляет рост объема продаж в результате изменения физического объема).
Допускается упрощенный вариант вывода: во столько-то раз в среднем возрос физический объем в отчетном периоде по сравнению с базисным.
2) Относительное отклонение, построенное на базе индекса физического объема, показывает, на сколько процентов (долей единицы) увеличился (уменьшился) объем продаж в отчетном периоде по сравнению с базисным из-за изменения физического объема.
Упрощенный вариант вывода: на столько-то процентов (долей единицы) в среднем увеличился (уменьшился) физический объем в отчетном периоде по сравнению с базисным.
Если индекс рассчитан в процентах, то:
Или
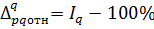
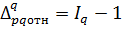
(8)
3) Абсолютное отклонение, построенное на базе индекса физического объема, показывает, на сколько рублей увеличился (уменьшился) объем продаж в отчетном периоде по сравнению с базисным из-за изменения физического объема.
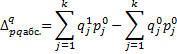
(9)
3. Агрегатный индекс цен. Цены на разную продукцию также могут быть несоизмеримыми. Например, цены на нефть и автомобиль. Если при измерении изменения цен цены на эти товары непосредственно складывать (без уравновешивания), то цена 1 барреля нефти «утонет» в цене автомашины; ею, казалось бы, можно было бы и пренебречь. Однако известно, насколько важна роль цен на нефть в ценообразовании стран и мира в целом.
При построении агрегатного индекса цен в качестве признака-веса выступает количество товаров, причем, в соответствии с правилом применения весов,- за отчетный период.
Тогда агрегатный индекс цен будет иметь следующий вид:
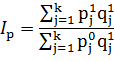
(10)
Построение агрегатных индексов с весами отчетного периода первым предложил немецкий экономист Г. Пааше (1874 г.), и с тех пор этот метод носит его имя.
Ответим на поставленные выше три вопроса.
1) Индекс цен показывает, во сколько раз возрос объем продаж в отчетном периоде по сравнению с базисным из-за изменения цен (или сколько процентов составляет рост объема продаж в результате изменения цен).
Упрощенный вариант вывода: во столько-то раз в среднем возросли цены в отчетном периоде по сравнению с базисным.
2) Относительное отклонение, построенное на базе индекса цен, показывает, на сколько процентов (долей единицы) увеличился
(уменьшился) объем продаж в отчетном периоде по сравнению с базисным из-за изменения цен.
Упрощенный вариант вывода: на столько-то процентов (долей единицы) в среднем выросли (снизились) цены в отчетном периоде по сравнению с базисным.
Или
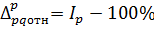
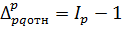
(11)
В макроэкономике относительное отклонение цен в динамике (в %) характеризует темп инфляции.
3) Абсолютное отклонение, построение на базе индекса цен, показывает, на сколько рублей увеличился (уменьшился) объем продаж в отчетном периоде по сравнению с базисным из-за изменения цен.
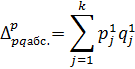
(12)
Между рассмотренными индексами существует взаимосвязь:
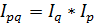
(13)
Абсолютные приросты, полученные на базе построенных индексов, также взаимосвязаны между собой:
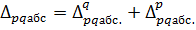
(14)
Аналогично строятся и другие агрегатные индексы (с учетом первичности появления признаков и соответствующего правила применения весов в индексе).
На примере построения и анализа агрегатных индексов можно было увидеть, что сводные индексы выполняют следующие функции:
1) Синтетическую, когда в одном индексе обобщаются (синтезируются) несоизмеримые явления.
2) Аналитическую, когда индексы – это показатели изменения уровня результативной величины под влиянием изменения индексируемой величины (признака-фактора)
Отметим, что для правильного расчета индексов требуются достаточно точные их измерения (в частности, для того, чтобы доказать взаимосвязь индексов). Поэтому индексы в процентной форме обычно рассчитывают до второго знака после запятой, а в коэффициентах – до четвертого знака после запятой.
Индексы цен Пааше, Ласпейреса, Фишера.
Их практическое применение
Выше была представлена методика построения и анализа индекса цен Пааше, в котором в качестве веса был взят физический объем отчетного периода (см. формулу 12):
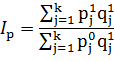
(15)
Однако в условиях инфляции, негативно изменяющейся рыночной структуры, когда «выматывается» дешевый товар, в анализе изменений на ценовом рынке при использовании индекса не учитываются, так как таких товаров нет в текущем периоде.
Для более реального отражения действительных изменений на ценовом рынке в мировой экономической практике ( в России- с 1991 г.) обычно применяют индекс цен, в котором в качестве веса используют базисный физический объем, т.е. этот индекс строится по методу Ласпейреса:
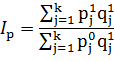
(16)
Таким образом, получили индекс цен Ласпейреса.
Значения индексов цен Пааше и Ласпейреса, конечно, не совпадают. Применение этих индексов определяется соответствующими экономическими условиями.
Индекс Пааше используют в макроэкономике в качестве индекса-дефлятора.
Индекс цен Ласпейреса учитывает изменение стоимости потребительской корзины, в связи с чем его еще называют «индексом стоимости жизни».
Индекс цен Пааше имеет некоторую тендецию занижения темпов инфляции, а индекс цен Ласпейреса – их завышения.
Следует отметить, что индексы цен Пааше и Ласперейса имеют определенную степень условности, так как рассчитываются или только по товарам отчетного периода, или только базисного. Однако даже, казалось бы, устойчивый набор потребительской корзины ( это касается индекса цен Ласперейса) должен в соответствии с современными требованиями жизни периодически пересматриваться.
Индекс цен Фишера ( И. Фишер- американский ученый ) – так называемый идеальный индекс цен, который представляет собой среднюю геометрическую из индексов Ласпейреса и Пааше:
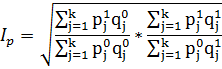
(17)
Отметим, что метод Фишера используется не только для построения индекса цен, но также может быть использован и для построения индекса физического объема:
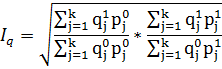
(18)
У геометрических индексов Фишера принципиальный недостаток: они не имеют конкретного экономического смысла. Так, в отличие от агрегатных индексов Ласпейреса и Пааше, разность между числителем и знаменателем не покажет никакой реальной экономии (или потерь) из-за изменения цен или физического объема продукции.
Индекс цен Фишера в силу сложности расчета и трудности экономической интерпретации на практике используется довольно редко. Обычно индекс цен Фишера применяется при измерении изменения цен за длительный период времени с целью сглаживания тенденций в структуре и составе объема продукции, в которых происходят значительные изменения.
Тест
Индекс – это:
а) указатель, реестр имен, названий и т.п.
б) числовой или буквенный указатель, используемый в математических выражениях и формулах;
в) показатель сравнения двух состояний во времени или в пространстве одного и того же явления (признака).
2. В общем индексе физического объема продукции весами (соизмерителями) являются:
а) количества продукции базисного периода;
б) количества продукции отчетного периода;
в) цены базисного периода;
г) цены отчетного периода.
3. В общем индексе цен весами являются:
а) количества продукции базисного периода;
б) количества продукции отчетного периода;
в) цены базисного периода;
г) цены отчетного периода.
4. Укажите, какой из индексов является среднеарифметическим индексом физического объема продукции, тождественного агрегатной форме:
а) ; б) ; в) ; г).
5. Укажите, какой из индексов является среднегармоническим индексом цен, тождественным агрегатной форме:
а) ; б) ; в) ; г).
6. Какие факторы оказывают влияние на индекс физического объема переменного состава:
а) изменение количества произведенной продукции;
б) изменение структуры цен;
в) изменение количества произведенной продукции и структуры цен.
7. Какой индекс позволяет определить изменение индексируемого признака:
а) индекс постоянного состава;
б) индекс переменного состава;
в) индекс структурных составов.
8. Какой индекс позволяет элиминировать влияние структурных сдвигов:
а) индекс структурных сдвигов;
б) индекс переменного состава;
в) индекс постоянного состава.
Дата добавления: 2020-12-22; просмотров: 470; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
