Статистические оценки параметров распределения

Статистическое распределение выборки

Пусть из генеральной совокупности извлечена выборка объема п:

значение x₁ некоторого исследуемого признака Х наблюдалось п₁ раз,

значение x₂ — п₂ раз, ..., значение x _k — n_k раз.

Значения x_i называются вариантами, а их последовательность, записанная в возрастающем порядке,— вариационным рядом. Числа n_i называются частотами, а их отношения к объему выборки

— относительными частотами. При этом 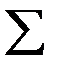n_i = п.

Кроме средних величин, называемых аналитическими, в статистическом анализе применяют структурные и порядковые средние. Из них наиболее широко применяются медиана и мода

Модой М_o называется варианта, имеющая наибольшую частоту.

Медианой т_е называется варианта, которая делит вариационный ряд на две части с одинаковым числом вариант в каждой. (для вариационного ряда с нечетным числом членов медиана равна серединному варианту, а для ряда с четным числом членов – полусумме двух серединных вариантов).

Размахом варьирования называется разность между максимальной и минимальной вариантами или длина интервала, которому принадлежат все варианты выборки:

Перечень вариант и соответствующих им частот называется статистическим распределением выборки.

Сумма относительных частот равна единице: 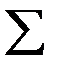W_i = 1.

Пример 2. Выборка задана в виде распределения частот:

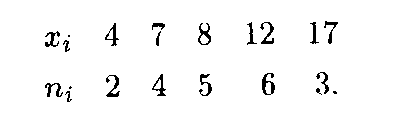
Найти распределение относительных частот и основные характеристики вариационного ряда.

Решение. Найдем объем выборки: п = 2 + 4 + 5 + 6 + 3 = 20. Относительные частоты соответственно равны W₁ = 2/20 = 0,1; W₂ = 4/20 = 0,2; W₃ = 5/20 = 0,25; W₄ = 6/20 = 0,3; W₅ = 3/20 = 0,15. Контроль: 0,1 + 0,2 + 0,25 + 0,3 + 0,15 = 1. Искомое распределение относительных частот имеет вид

Мода этого вариационного ряда равна 12. медиана m_e = x₃ = 8. Размах варьирования, согласно формуле (18.48),

R = 17 – 4 = 13.

Пример 3. Найти медиану распределения рабочих по тарифному разряду

Тарифный разряд	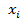1	2	3	4	5	6
Частота (количество рабочих)	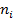2	3	6	8	22	9	50

Решение. n = 50 - четное, следовательно, серединных вариантов два: 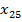= 5 и

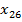=5. Поэтому = = =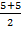5

Эмпирическая функция распределения

Пусть n_х — число наблюдений, при которых значение признака Х меньше х. При объеме выборки, равном п, относительная частота события Х < х равна n_x/n.

Определение. Функция

( = ,

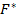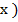определяющая для каждого значения х относительную частоту события Х < х, называется эмпирической функцией распределения, или функцией распределения выборки.

В отличие от эмпирической функции распределения F *( x ) выборки функция распределения F ( x ) генеральной совокупности называется теоретической функцией распределения. Различие между ними состоит в том, что функция F ( x ) определяет вероятность события Х < х, a F *( x ) — относительную частоту этого события.

Нетрудно видеть, что F *( x ) обладает всеми свойствами F ( x ) 1) значения F *( x ) принадлежат отрезку [0, 1];

2) F *( x ) является неубывающей функцией;

3) если х₁ — наименьшая варианта, то F *( x ) = 0 при х ≤ х₁; если x_k — максимальная варианта, то F *( x ) = 1 при x > x _k .

Сама же функция F *( x ) служит для оценки теоретической функции распределения F ( x ) генеральной совокупности.

Пример 4. Построить эмпирическую функцию по заданному распределению выборки:

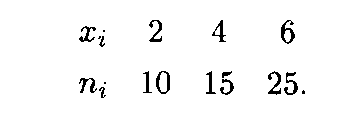
Решение. Находим объем выборки: п = 10 + 15 + 25 = 50. Наименьшая варианта равна 2, поэтому F *( x ) = 0 при х ≤ 2. Значение Х < 4 (или x₁ = 2) наблюдалось 10 раз, значит, F *( x ) = 10/50 = 0,2 при 2 < х 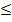4. Значения X < 6 (а именно x₁ = 2 и x₂ = 4) наблюдались 10 + 15 = 25 раз, значит, при 4 < х 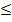6 функция F *( x ) = 25/50 = 0,5. Поскольку x = 6 — максимальная варианта, то F *( x ) = 1 при х > 6. Напишем формулу искомой эмпирической функции:

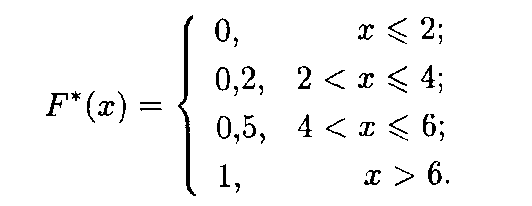
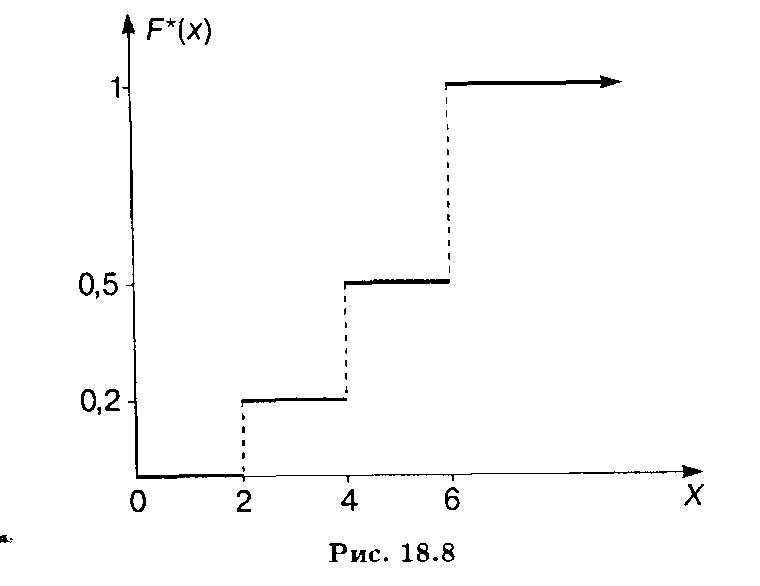
График этой функции показан на рис. 18.8.

Полигон и гистограмма

Ломаная, отрезки которой соединяют точки (x_i , n_i), называется полигоном частот. Ломаная, соединяющая на координатной плоскости точки (x_i , W_i), называется полигоном относительных частот. На рис. 18.9 показан полигон относительных частот для распределения, приведенного в примере 2.

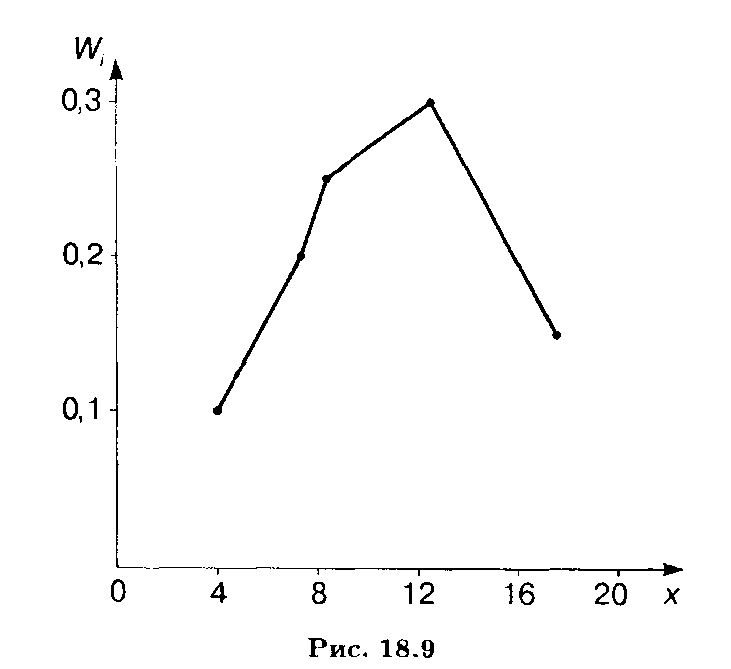
Для случая непрерывного признака Х удобно разбить интервал (x_min, x_max) его наблюдаемых значений на несколько частичных интервалов длиной h каждый и найти для каждого из этих интервалов сумму частот n_j, попавших в него. Ступенчатая фигура, состоящая из прямоугольников с основаниями длиной h и высотами n_j / h (плотность частоты), называется гистограммой частот.

Геометрический смысл гистограммы: площадь ее равна сумме всех частот или объему выборки.

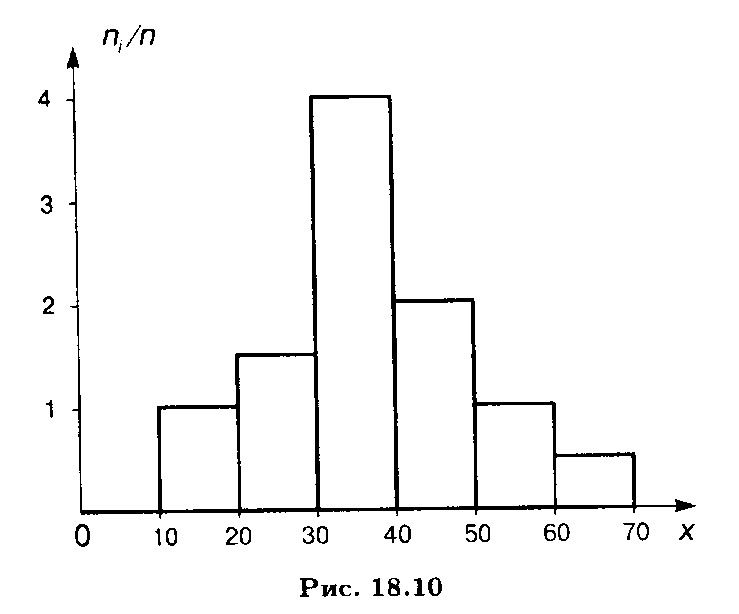
На рис. 18.10 изображена гистограмма объема n = 100.

Аналогичным образом определяется и гистограмма относительных частот: в этом случае высоты прямоугольников, составляющих ступенчатую фигуру, определяются отношениями сумм относительных частот, попадающих в интервал (x_min + (j — 1)h, x_min + jh), к длине интервала h, т.е. величинами W_j / h . Нетрудно видеть, что площадь гистограммы относительных частот равна единице (сумме относительных частот выборки).

Статистические оценки параметров распределения

Значения количественного признака х₁, х₂, ..., х_k в выборке можно рассматривать как независимые случайные величины. В таком случае нахождение статистической оценки неизвестного параметра теоретического распределения означает отыскание функции от наблюдаемых случайных величин, которая и даст нам приближенное значение искомого параметра. Укажем виды статистических оценок.

Несмещенной называется статистическая оценка 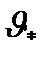, математическое ожидание которой равно оцениваемому параметру при любой выборке:

Смещенной называется оценка, при которой условие (18.51) не выполнено. Эффективной называется оценка, которая имеет минимальную дисперсию при заданном объеме выборки п. Состоятельной называется статистическая оценка типа (18.50), которая при п > стремится по вероятности к оцениваемому параметру.

Виды числовых характеристик оценок.

Если значения признака х₁, x₂, …, х_k в выборке имеют соответственно частоты n₁, n₂, ..., n_k , то выборочная средняя

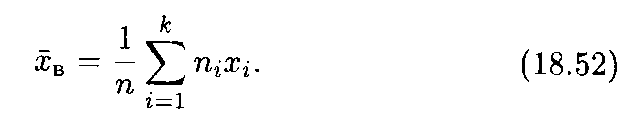
Выборочная средняя (18.52) является несмещенной оценкой; это аналог математического ожидания случайной величины.

Величина, характеризующая отклонение значений количественного признака Х от своего среднего значения это

выборочная дисперсия:

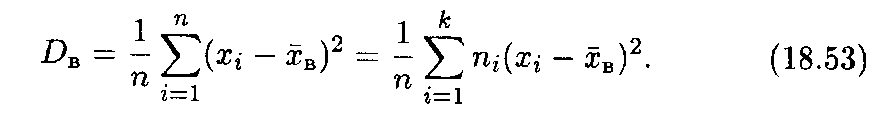
Для вычисления этой характеристики справедлива более удобная формула, аналогичная дисперсии случайной величины; так, формула (18.53) принимает вид

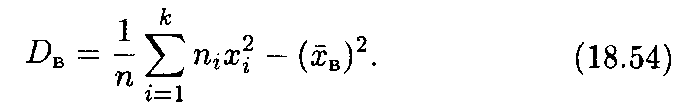
Выборочное среднее квадратическое отклонение

Пример 4. Выборка задана таблицей распределения

Найти выборочные характеристики: среднюю, дисперсию и среднее квадратическое отклонение.

Решение. По формуле (18.52) сначала находим 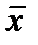_в:

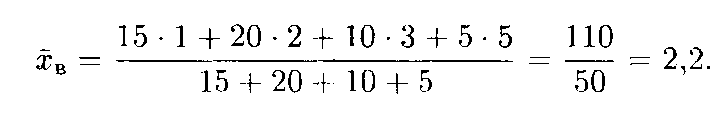
Затем по формулам (18.54) и (18.55) находим две другие искомые величины:

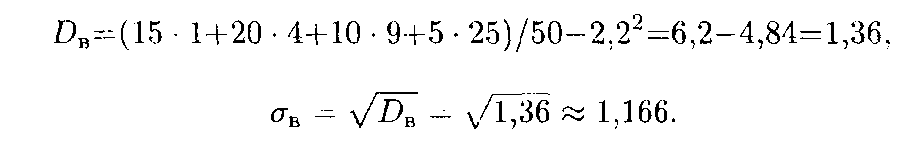
Дата добавления: 2020-12-22; просмотров: 199; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!