Простейшие логарифмические уравнения и сводящиеся к ним
Логарифмические уравнения и системы уравнений.
Конспект урока
Логарифмические уравнения
Для решения логарифмических уравнений и неравенств нам понадобятся определение и свойства логарифмов.
Определение: 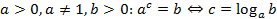 .
.
Эквивалентная запись определения или основное логарифмическое тождество:
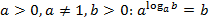 .
.
Свойства:
1) 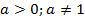 :
:  ,
, 
2)  ,
,  для
для 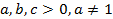
3)  ,
,  для
для 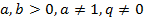
4) Формула перехода к новому основанию: 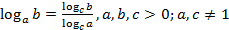 .
.
Рассмотрим логарифмическую функцию: 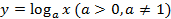 .
.
Мы уже знаем её область определения:  , так как показательное уравнение
, так как показательное уравнение 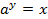 (урок «Логарифмы») не имеет решений при
(урок «Логарифмы») не имеет решений при 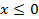 .
.
Рассмотрим графики логарифмической функции при основании, большем 1, и основании от 0 до 1:
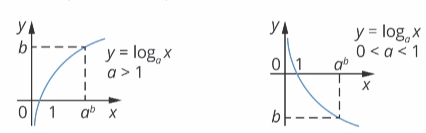
Графики иллюстрируют такие свойства логарифмической функции:
1) 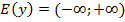 .
.
2) При 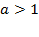 функция монотонно возрастает на всей области определения (обратите внимание на сходство с показательной функцией).
функция монотонно возрастает на всей области определения (обратите внимание на сходство с показательной функцией).
При 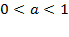 функция монотонно убывает на всей области определения.
функция монотонно убывает на всей области определения.
Рассмотрим простейшее логарифмическое уравнение: 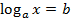 (
( 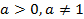 ). Нарисуем на координатной плоскости график логарифмической функции. Решением этого уравнения будет пересечение этого графика с горизонтальной прямой
). Нарисуем на координатной плоскости график логарифмической функции. Решением этого уравнения будет пересечение этого графика с горизонтальной прямой 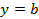 .
.

Мы видим, что при любом 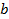 данное уравнение имеет единственное решение (так как логарифмическая функция монотонна). Найти решение этого уравнения можно, используя определение логарифма:
данное уравнение имеет единственное решение (так как логарифмическая функция монотонна). Найти решение этого уравнения можно, используя определение логарифма:  . Но можно использовать и метод, который мы применяли для решения простейших показательных уравнений, а именно: представить правую часть в виде логарифма с тем же основанием, что и в левой части:
. Но можно использовать и метод, который мы применяли для решения простейших показательных уравнений, а именно: представить правую часть в виде логарифма с тем же основанием, что и в левой части:  . И приравнять подлогарифмические выражения.
. И приравнять подлогарифмические выражения.
|
|
|
Рассмотрим пример: 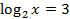 . Используя определение логарифма, получим:
. Используя определение логарифма, получим:  . Чтобы решить это же уравнение вторым способом, необходимо представить правую часть в виде логарифма с основанием 2. Как это сделать? Для этого используют универсальный метод, а именно:
. Чтобы решить это же уравнение вторым способом, необходимо представить правую часть в виде логарифма с основанием 2. Как это сделать? Для этого используют универсальный метод, а именно: 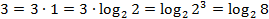 .
.
Тогда 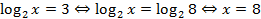 . То есть в общем виде: если мы хотим представить
. То есть в общем виде: если мы хотим представить 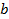 в виде логарифма с основанием
в виде логарифма с основанием 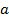 , то мы расписываем
, то мы расписываем  , то есть заменяем 1 на
, то есть заменяем 1 на 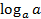 (урок «Логарифмы»). А дальше вносим множитель перед логарифмом в показатель степени (урок «Логарифмы»):
(урок «Логарифмы»). А дальше вносим множитель перед логарифмом в показатель степени (урок «Логарифмы»): 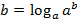 .
.
Показательная функция  определена при всех значениях переменной. А логарифмическая
определена при всех значениях переменной. А логарифмическая  только при положительных:
только при положительных: 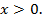 Поэтому при решении логарифмических уравнений необходимо помнить, что
Поэтому при решении логарифмических уравнений необходимо помнить, что 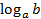 имеет смысл только при
имеет смысл только при 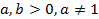 .
.
Таким образом, при решении логарифмических уравнений необходимо либо учитывать ОДЗ (проверять, входят ли полученные корни в него), либо в конце решения сделать проверку. Чаще всего выполнить проверку проще.
Любое более сложное логарифмическое уравнение решается «выливанием воды из чайника», то есть сведением его различными методами к простейшим. Этих методов немного, все они основаны на использовании определения и свойств логарифма. И все эти методы мы рассмотрели на прошлом уроке, выполняя преобразования выражений, содержащих логарифмы.
|
|
|
Таким образом, можно выделить следующие инструменты для решения логарифмических уравнений:
1) Сведение логарифмического уравнения к простейшему.
2) Решение простейшего логарифмического уравнения.
3) Проверка корней (подставить или проверить ОДЗ).
При решении простейших логарифмических уравнений могут возникать линейные, квадратные, иррациональные, показательные уравнения – то есть все те уравнения, которые мы уже умеем решать.
Перейдём теперь к использованию перечисленных инструментов на практике.
Простейшие логарифмические уравнения и сводящиеся к ним
Пример 1
Решить уравнение:  .
.
Мы решаем простейшее логарифмическое уравнение. Используем определение логарифма: 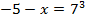 , откуда:
, откуда: 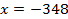 . Выполняем проверку:
. Выполняем проверку:
 - верно.
- верно.
Обратите внимание, что при проверке мы подставляем полученные значения переменной в исходное уравнение.
Ответ: 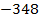 .
.
Пример 2
Решить уравнение: 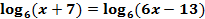 .
.
В левой и правой части стоят логарифмы с одинаковыми основаниями, значит, можем приравнять подлогарифмические выражения:
|
|
|

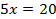
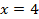
Проверка: 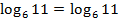 - верно.
- верно.
Ответ: 4
Пример 3
Решить уравнение:  .
.
Это не совсем обычное простейшее уравнение, так как в нём переменная находится в основании логарифма. Но это не должно вас пугать. Как и для обычного простейшего логарифмического уравнения, воспользуемся определением логарифма: 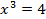 . По определению корня, получаем:
. По определению корня, получаем: 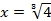 . Получили положительное число, не равное 1, – значит, оно может быть основанием логарифма.
. Получили положительное число, не равное 1, – значит, оно может быть основанием логарифма.
Ответ:  .
.
Пример 4
Решить уравнение: 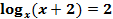 .
.
И снова не совсем обычное простейшее логарифмическое уравнение: переменная находится и в основании логарифма, и в подлогарифмическом выражении. Но суть решения от этого не меняется – используем определение логарифма: 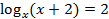 .
.
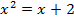
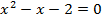

Выполняем проверку: 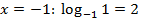 – не подходит (основание логарифма не может быть отрицательным).
– не подходит (основание логарифма не может быть отрицательным).
 - верно.
- верно.
Ответ: 2.
Пример 5
Решить уравнение: 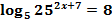 .
.
И снова используем определение логарифма: 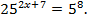
Получили показательное уравнение, которое мы уже умеем решать. Необходимо обе части привести к одному основанию: 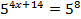 .
.
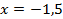
Проверка: 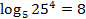 – верно.
– верно.
Ответ: -1,5.
Рассмотрим решение уравнений с использованием свойств логарифмов
Пример 6
Решить уравнение: 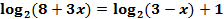 .
.
|
|
|
Необходимо свести это уравнение к простейшему. Это можно сделать двумя способами:
· перенести логарифм из правой части в левую: 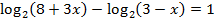 .
.
Откуда, используя свойства логарифмов: 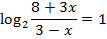 . Далее необходимо использовать определение логарифма.
. Далее необходимо использовать определение логарифма.
· представить обе части в виде логарифмов с основанием 2.
Для этого воспользоваться рассмотренным ранее универсальным приёмом: 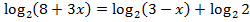 – и свойством логарифмов:
– и свойством логарифмов:  . Далее можно приравнять подлогарифмические выражения.
. Далее можно приравнять подлогарифмические выражения.
При решении любым из способов получится:
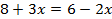
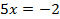
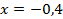
Проверка: 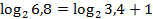 – верно.
– верно.
Ответ: 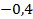 .
.
Пример 7
Решить уравнение: 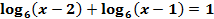 .
.
В левой части стоит сумма двух логарифмов с одинаковыми основаниями, поэтому сразу преобразуем её в логарифм произведения: 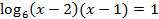 . Получили простейшее уравнение, которое решаем, используя определение логарифма:
. Получили простейшее уравнение, которое решаем, используя определение логарифма:
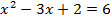
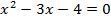
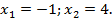
Проверка:
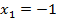 – не подходит (под логарифмом не могут стоять отрицательные выражения).
– не подходит (под логарифмом не могут стоять отрицательные выражения).
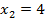 – подходит.
– подходит.
Ответ: 4.
Пример 8
Решить уравнение:  .
.
Это уравнение можно сводить к простейшему по-разному. Поскольку в левой части стоит отношение двух логарифмов с одинаковыми основаниями, напрашивается использование формулы перехода к новому основанию:  . Получили иррациональное уравнение, которое мы уже умеем решать.
. Получили иррациональное уравнение, которое мы уже умеем решать.
Но можно приводить к простейшему это же уравнение и по-другому, если воспользоваться правилом пропорции: 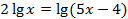 . Чтобы получить слева десятичный логарифм (а затем приравнять подлогарифмические выражения), необходимо внести 2 в показатель степени:
. Чтобы получить слева десятичный логарифм (а затем приравнять подлогарифмические выражения), необходимо внести 2 в показатель степени:

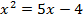
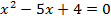
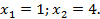
Проверка:
 – не подходит.
– не подходит.
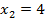 – подходит.
– подходит.
Ответ: 4.
Пример 9
Решить уравнение: 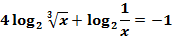 .
.
Как и в заданиях на преобразование выражений с логарифмами, первым делом избавимся от показателей степени под логарифмами:
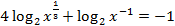


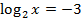
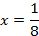
Проверка:  – верно.
– верно.
Ответ:  .
.
Если переменная встречается в уравнении в одном и том же выражении с логарифмом, то с помощью замены можно свести логарифмическое уравнение к одному из тех, которые мы уже умеем решать (дробно-рациональному, иррациональному, показательному и т.д.).
Пример 1
Решить уравнение:  .
.
Видим, что переменная в уравнении встречается только в выражении  . Поэтому с помощью замены
. Поэтому с помощью замены 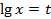 сводим уравнение к дробно-рациональному:
сводим уравнение к дробно-рациональному: 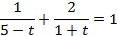 .
.
Такие уравнения мы уже умеем решать: переносим 1 влево и приводим все дроби к общему знаменателю: 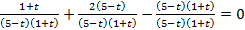 .
.
ОДЗ: 
Приравниваем числитель дроби к 0 (знаменатель не равен 0).
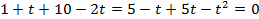
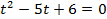
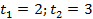
Обратная замена:
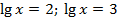

Проверка:
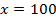 – подходит.
– подходит.
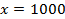 – подходит.
– подходит.
Ответ: 100, 1000.
Пример 2
Решить уравнение: 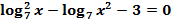 .
.
Как и раньше, в первую очередь избавляемся от показателей степени под логарифмом:  . Можем выносить чётную степень, так как
. Можем выносить чётную степень, так как  (ОДЗ первого логарифма).
(ОДЗ первого логарифма).
Теперь переменная встречается только в выражении 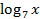 . Выполняем замену:
. Выполняем замену:  .
.
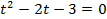

Обратная замена:
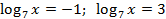
 .
.
Проверка:
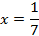 – подходит.
– подходит.
 – подходит.
– подходит.
Ответ:  ;
; 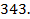
Подведём краткие итоги. Для решения рассмотренных примеров нам необходимо следующее.
Знать
Определение и свойства логарифмов.
Уметь
Решать простейшие логарифмические уравнения.
Понимать
В конце решения логарифмических уравнений необходимо выполнить проверку или в начале решения проверить ОДЗ.
Дата добавления: 2020-12-22; просмотров: 102; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
