Глава 3. Материалы для практических занятий
Материалы для лекции и практического
1.1. Корни многочлена. Теорема Безу. Схема Горнера
Число c называют корнем многочлена  , если
, если 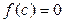 .
.
Справедлива теорема Безу.
Остаток от деления многочлена  на линейный двучлен
на линейный двучлен 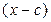 равен значению многочлена при
равен значению многочлена при 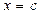 .
.
Число c тогда и только тогда является корнем многочлена  , когда
, когда  делится нацело на
делится нацело на 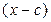 .
.
Число c называют k-кратным корнем многочлена  , если
, если  делится на
делится на  , но не делится на
, но не делится на 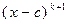 .
.
Если  , то коэффициенты многочлена
, то коэффициенты многочлена 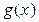 и остаток r могут быть найдены по схеме Горнера:
и остаток r могут быть найдены по схеме Горнера:
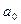
| 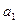
| 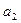
| … | 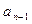
| 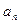
| |
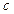
| 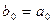
| 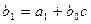
| 
| … | 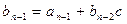
| 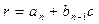
|
где 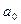 ,
, 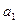 , …,
, …, 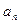 – коэффициенты многочлена
– коэффициенты многочлена  , записанного по убывающим степеням x:
, записанного по убывающим степеням x:
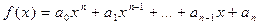 , а
, а
 .
.
Задача №6
Найти кратность корня x = 5 многочлена:  .
.
Решение.
Используя схему Горнера, имеем:
| 1 | – 15 | 76 | – 140 | 75 | – 125 | |
| 5 | 1 | – 10 | 26 | – 10 | 25 | 0 |
Получим, что 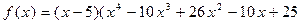 ).
).
Число 5 является корнем  . Если 5 будет корнем и
. Если 5 будет корнем и 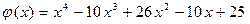 , то 5 будет корнем многочлена
, то 5 будет корнем многочлена  второй кратности или выше.
второй кратности или выше.
Проверим, будет ли 5 корнем многочлена 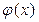 по схеме Горнера:
по схеме Горнера:
| 1 | – 10 | 26 | – 10 | 25 | |
| 5 | 1 | – 5 | 1 | – 5 | 0 |
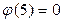 , следовательно, 5 – корень
, следовательно, 5 – корень 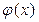 .
.
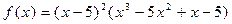 .
.
Проверим, будет ли число 5 корнем многочлена  .
.
| 1 | – 5 | 1 | – 5 | |
| 5 | 1 | 0 | 1 | 0 |
Число 5 является корнем 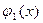 , отсюда имеем:
, отсюда имеем:
 , а
, а  .
.
Число 5 корнем многочлена 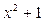 уже не является. Следовательно,
уже не является. Следовательно,  делится на
делится на 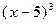 , но не делится на
, но не делится на 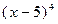 . Значит, кратность корня 5 многочлена
. Значит, кратность корня 5 многочлена  равна 3.
равна 3.
|
|
|
Процесс решения можно оформить следующим образом:
| 1 | – 15 | 76 | – 140 | 75 | – 125 | |
| 5 | 1 | – 10 | 26 | – 10 | 25 | 0 |
| 5 | 1 | – 5 | 1 | – 5 | 0 | |
| 5 | 1 | 0 | 1 | 0 | ||
| 5 | 1 | 5 | 26¹0 |
Число 5 является трехкратным корнем многочлена 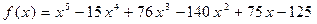 , т.е.
, т.е.  .
.
Задача №7
Остатки от деления многочлена  на x – 2 и x – 3 равны соответственно 5 и 7. Найти остаток от деления этого многочлена на
на x – 2 и x – 3 равны соответственно 5 и 7. Найти остаток от деления этого многочлена на  .
.
Решение.
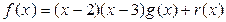
 , т.к. степень делителя
, т.к. степень делителя  равна двум, то степень остатка
равна двум, то степень остатка 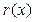 меньше или равна единице, т.е.
меньше или равна единице, т.е.  .
.
По теореме Безу имеем 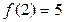 ,
, 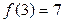 .
.
При x = 2 равенство  принимает вид
принимает вид 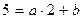 ,
,
При x = 3 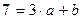 .
.
Решая систему  получаем a = 2, b = 1.
получаем a = 2, b = 1.
Итак, 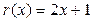 .
.
Задача №8
Найти, при каких a и b многочлен  делится на
делится на 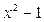 .
.
Решение.
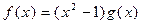 .
.
При x = 1 имеем  ,
,
При x = – 1 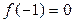 , получаем систему
, получаем систему
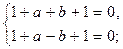
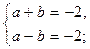 отсюда a = – 2, b = 0.
отсюда a = – 2, b = 0.
Задача №9
Пользуясь схемой Горнера, разложить многочлен  по степеням x – 1, найти значение многочлена
по степеням x – 1, найти значение многочлена  и всех его производных при x = 1.
и всех его производных при x = 1.
Решение.
По формуле Тейлора имеем:
 - разложение многочлена
- разложение многочлена  по степеням x – 1.
по степеням x – 1.
Как видно из формулы, для решения задачи нужно найти значения многочлена  и его производных при x = 1. Это можно сделать непосредственно, находя производные многочлена
и его производных при x = 1. Это можно сделать непосредственно, находя производные многочлена  , а затем их значения при x = 1.
, а затем их значения при x = 1.
|
|
|
Но для решения этой задачи можно использовать также и схему Горнера. Запишем разложение многочлена  по степеням (x – 1) с неопределенными коэффициентами:
по степеням (x – 1) с неопределенными коэффициентами:
 .
.
Числа 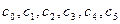 равны соответственно остаткам от деления многочленов
равны соответственно остаткам от деления многочленов  ,
, 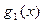 ,
, 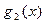 ,
,  ,
, 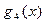 ,
, 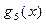 на x – 1, где
на x – 1, где 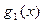 есть частное от деления
есть частное от деления  на x – 1,
на x – 1, 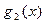 есть частное от деления
есть частное от деления 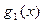 на
на 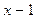 и т.д. Наконец,
и т.д. Наконец, 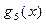 есть частное от деления
есть частное от деления 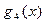 на x – 1.
на x – 1.
Все решения можно записать в схему:
| 1 | 3 | 0 | 0 | 2 | -4 | |
| 1 | 1 | 4 | 4 | 4 | 6 | 2 |
| 1 | 1 | 5 | 9 | 13 | 19 | |
| 1 | 1 | 6 | 15 | 28 | ||
| 1 | 1 | 7 | 22 | |||
| 1 | 1 | 8 | ||||
| 1 | 1 |
Отсюда  ,
,  ,
, 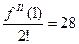 ,
, 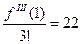 ,
,  ,
, 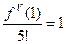 , тогда
, тогда  ,
,  ,
,  ,
, 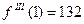 ,
, 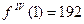 ,
, 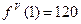 .
.
Подставляем найденные значения в формулу Тейлора, имеем: 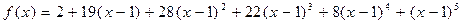 .
.
Задача №10
Разложить на простейшие дроби рациональную дробь 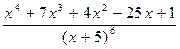 .
.
Решение.
Разложим числитель 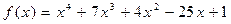 по степеням x + 5 по формуле Тейлора, используя схему Горнера.
по степеням x + 5 по формуле Тейлора, используя схему Горнера.
| 1 | 7 | 4 | – 25 | 1 | |
| – 5 | 1 | 2 | – 6 | 5 | – 24 |
| – 5 | 1 | – 3 | 9 | – 40 | |
| – 5 | 1 | – 8 | 49 | ||
| – 5 | 1 | – 13 | |||
| – 5 | 1 |
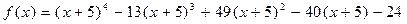 .
.
|
|
|
Тогда 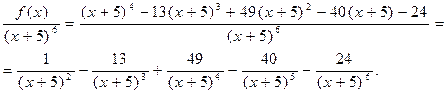
Задача №11
Вычислить значение многочлена 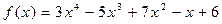 при
при  .
.
Решение.
Ближайшим целым числом к 4,99 является 5, поэтому сначала разложим многочлен  по степеням x – 5 по формуле Тейлора, используя схему Горнера, а затем подставим значение x = 4,99.
по степеням x – 5 по формуле Тейлора, используя схему Горнера, а затем подставим значение x = 4,99.
| 3 | – 5 | 7 | – 1 | 6 | |
| 5 | 3 | 10 | 57 | 284 | 1426 |
| 5 | 3 | 25 | 182 | 1194 | |
| 5 | 3 | 40 | 382 | ||
| 5 | 3 | 55 | |||
| 5 | 3 |
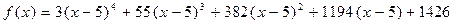 ;
;
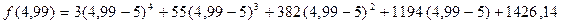
 ;
;
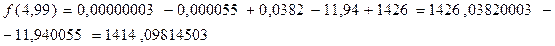
Итак, 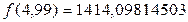 .
.
Глава 3. Материалы для практических занятий
В задачах 1 – 10 разделить с остатком многочлен  на
на 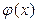 :
:
1. 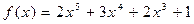 ,
, 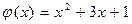 .
.
2. 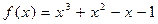 ,
, 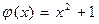 .
.
3. 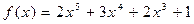 ,
, 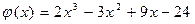 .
.
4. 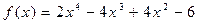 ,
, 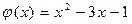 .
.
5. 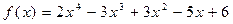 ,
, 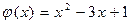 .
.
6. 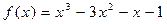 ,
,  .
.
7. 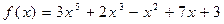 ,
, 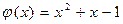 .
.
8.  ,
, 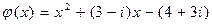 .
.
9. 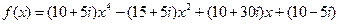 ,
,  .
.
10.  ,
, 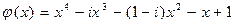 .
.
В задачах 11 – 20 найти необходимые и достаточные условия делимости многочлена  на
на 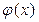 :
:
11. 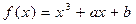 ,
, 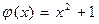 .
.
12. 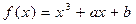 ,
, 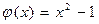 .
.
13.  ,
, 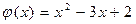 .
.
14. 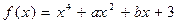 ,
, 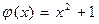 .
.
15. 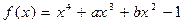 ,
, 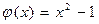 .
.
16. 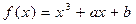 ,
, 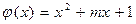 .
.
17. 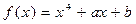 ,
, 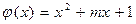 .
.
18. 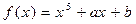 ,
, 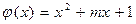 .
.
19. 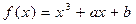 ,
,  .
.
20. 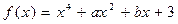 ,
, 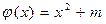 .
.
В задачах 21 – 30 найти наибольший делитель многочленов  и
и 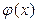 с помощью алгоритма Евклида:
с помощью алгоритма Евклида:
|
|
|
21. 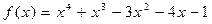 ,
, 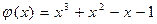 .
.
22. 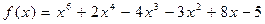 ,
, 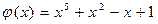 .
.
23. 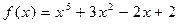 ,
, 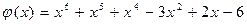 .
.
24. 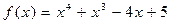 ,
, 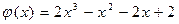 .
.
25. 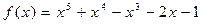 ,
, 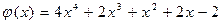 .
.
26. 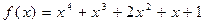 ,
,  .
.
27. 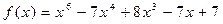 ,
,  .
.
28. 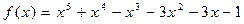 ,
,  .
.
29. 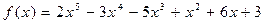 ,
, 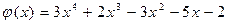 .
.
30. 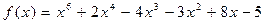 ,
, 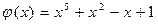 .
.
В задачах 31 – 40, пользуясь алгоритмом Евклида, найти многочлены 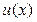 и
и  так, чтобы
так, чтобы 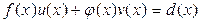 , где
, где 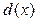 – наибольший общий делитель многочленов
– наибольший общий делитель многочленов  и
и  :
:
31. 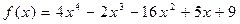 ,
, 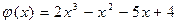 .
.
32.  ,
, 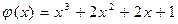 .
.
33.  ,
,  .
.
34. 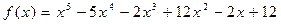 ,
, 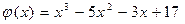 .
.
35. 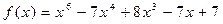 ,
, 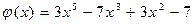 .
.
36. 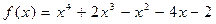 ,
, 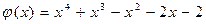 .
.
37.  ,
, 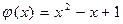 .
.
38. 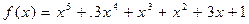 ,
, 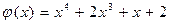 .
.
39. 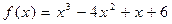 ,
, 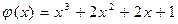 .
.
40. 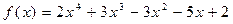 ,
, 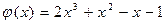 .
.
В заданиях 41–50, пользуясь схемой Горнера, разделить многочлен  на линейный двучлен
на линейный двучлен 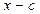 и найти значение многочлена
и найти значение многочлена  при
при 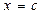 :
:
41. 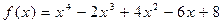 ,
,  .
.
42.  ,
, 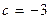 .
.
43. 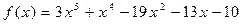 ,
, 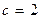 .
.
44.  ,
, 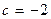 .
.
45.  ,
,  .
.
46. 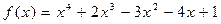 ,
, 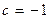 .
.
47.  ,
, 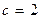 .
.
48. 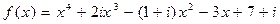 ,
, 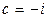 .
.
49.  ,
, 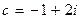 .
.
50.  ,
, 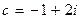 .
.
В задачах 51 – 55 найти остаток от деления многочлена  на
на 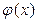 , не применяя теорему о делении с остатком:
, не применяя теорему о делении с остатком:
51. 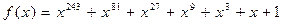 ,
, 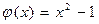 .
.
52. 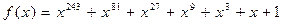 ,
,  .
.
53. 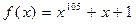 ,
, 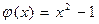 .
.
54. 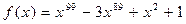 ,
,  .
.
55. 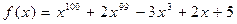 ,
, 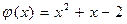 .
.
56. Многочлен 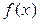 при делении на
при делении на 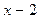 и
и 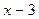 дает соответственно остатки 5 и 7. Найти остаток от деления этого многочлена на
дает соответственно остатки 5 и 7. Найти остаток от деления этого многочлена на 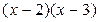 .
.
57. При делении 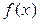 на
на 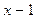 ,
, 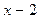 и
и 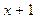 остатки соответственно равны 3, 15 и 0. Найти остаток от деления
остатки соответственно равны 3, 15 и 0. Найти остаток от деления 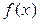 на
на 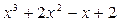 .
.
58. Многочлен 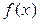 при делении на
при делении на 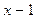 ,
, 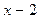 ,
, 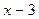 и на
и на 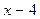 дает соответственно остатки 1, 3, 5 и 6. Найти остаток при делении этого многочлена на произведение
дает соответственно остатки 1, 3, 5 и 6. Найти остаток при делении этого многочлена на произведение  .
.
59. Найти при каких значения a многочлен 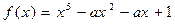 делится на
делится на 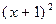 .
.
60. При каких значения a и b многочлен 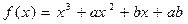 при делении на
при делении на 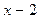 дает остаток 15, а при делении на
дает остаток 15, а при делении на 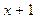 – остаток 0?
– остаток 0?
В задачах 61 – 70 найти кратность корня 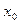 для многочлена
для многочлена 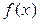 .
.
61. 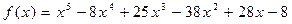 ,
, 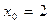 .
.
62.  ,
, 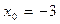 .
.
63. 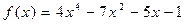 ,
,  .
.
64. 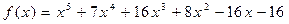 ,
, 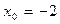 .
.
65.  ,
, 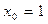 .
.
66. 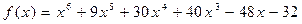 ,
, 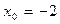 .
.
67.  ,
, 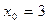 .
.
68. 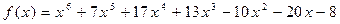 ,
, 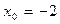 .
.
69. 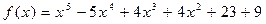 ,
, 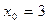 .
.
70.  ,
, 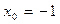 .
.
В задачах 71 – 80, пользуясь схемой Горнера, разложить многочлен 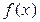 по степеням
по степеням 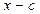 . Найти значения многочлена
. Найти значения многочлена  и его производных при
и его производных при 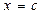 .
.
71. 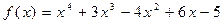 ,
, 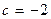 .
.
72. 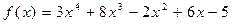 ,
, 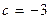 .
.
73. 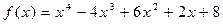 ,
, 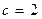 .
.
74.  ,
, 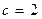 .
.
75.  ,
, 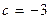 .
.
76. 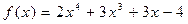 ,
, 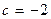 .
.
77. 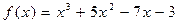 ,
, 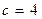 .
.
78.  ,
, 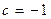 .
.
79.  ,
, 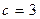 .
.
80.  ,
, 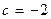 .
.
В задачах 81 – 90 разложить на простейшие дроби данные рациональные дроби:
81.  .
82. .
82. 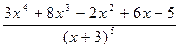 .
83. .
83. 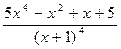 .
84. .
84.  .
85. .
85.  . .
| 86.  .
87. .
87. 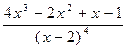 .
88. .
88. 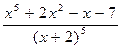 .
89. .
89. 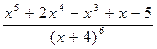 .
90. .
90. 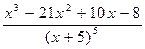 . .
|
Дата добавления: 2020-11-29; просмотров: 288; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
