Свойства определенного интеграла.
17.11.2020; 11.10 -12.45
Математический анализ.
Лекция 11.
Интегральное исчисление
Первообразная функции. Неопределенный интеграл и его свойства. Таблица неопределенных интегралов.
Определение. Функция 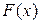 называется первообразной функции
называется первообразной функции 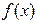 на интервале
на интервале 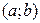 , если для всех x из
, если для всех x из 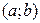 выполняется равенство
выполняется равенство 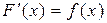 .
.
Аналогично вводится понятие первообразной для других множеств (отрезка, полуинтервала и т.д.). Легко видеть, что функция 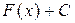 , где C –– константа, тоже будет первообразной для
, где C –– константа, тоже будет первообразной для 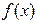 :
:  . Справедливо и обратное утверждение.
. Справедливо и обратное утверждение.
Теорема. Пусть 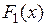 и
и 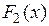 –– любые первообразные для функции
–– любые первообразные для функции 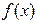 на
на 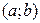 . Тогда существует такая константа C , что
. Тогда существует такая константа C , что 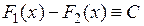 на
на 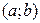 .
.
Доказательство. Введем функцию  . Производная этой функции равна нулю на
. Производная этой функции равна нулю на 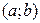 :
: 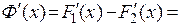
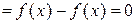 .
.
Пусть  –– любая, но фиксированная точка интервала
–– любая, но фиксированная точка интервала 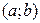 , а x –– любая вторая точка интервала
, а x –– любая вторая точка интервала 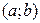 . По теореме Лагранжа имеем:
. По теореме Лагранжа имеем:
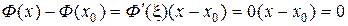 .
.
В последней формуле  –– точка, расположенная между x и
–– точка, расположенная между x и  . Введем обозначение:
. Введем обозначение: 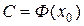 . Тогда
. Тогда 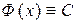 , т.е.
, т.е. 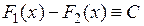 .
.
Теорема доказана.
Тем самым установлен следующий результат. Пусть 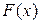 –– первообразная
–– первообразная 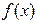 на
на 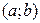 . Тогда любая первообразная
. Тогда любая первообразная 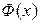 для
для 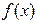 представима в виде:
представима в виде: 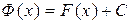 , где C –– некоторое число.
, где C –– некоторое число.
Определение. Совокупность всех первообразных для функции 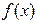 на
на 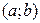 называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 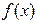 и обозначается символом
и обозначается символом  . При этом знак
. При этом знак 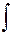 называется знаком интеграла, выражение
называется знаком интеграла, выражение 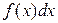 называется подынтегральным выражением, а
называется подынтегральным выражением, а 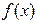 называется подынтегральной функцией.
называется подынтегральной функцией.
|
|
|
Полученные выше результаты позволяют записать
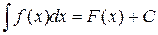 ,
,
где 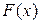 –– какая-то (любая, но фиксированная) первообразная функция
–– какая-то (любая, но фиксированная) первообразная функция 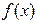 на
на 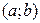 , а C –– любая константа.
, а C –– любая константа.
Свойства неопределенного интеграла.
1.  .
.
2.  .
.
3. 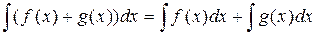 .
.
4. 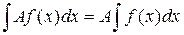 , где A –– любое число.
, где A –– любое число.
Доказательство свойства 1:
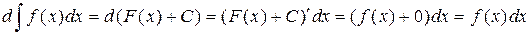 .
.
При вычислении была использована формула для дифференциала функции: 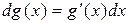 .
.
Равенства 3, 4 понимаются особым образом. И левая часть, и правая часть этих равенств есть множества функций. Равенства означают, что любая функция из множества левой части равенства отличается от любой функции из множества правой части равенства на число (на постоянное слагаемое).
Доказательство свойств 3, 4 основано на факте, который был использован при доказательстве теоремы: если производные двух функций на интервале  совпадают, то эти функции отличаются на постоянное слагаемое.
совпадают, то эти функции отличаются на постоянное слагаемое.
Доказательство свойства 3:
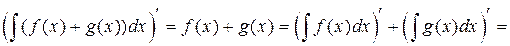
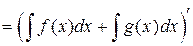 .
.
Мы получим, что производная левой части равна производной правой части. Свойство 3 доказано.
Таблица неопределенных интегралов.
1. 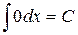 .
.
2. 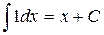 .
.
3.  ,
,  .
.
4.  ,
, 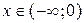 ,
, 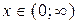 .
.
5.  ,
, 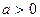 ,
, 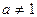 .
.
6. 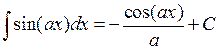 ,
,  .
.
7. 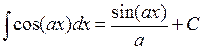 ,
,  .
.
8. 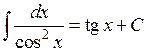 ,
,  ,
, 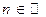 .
.
9. 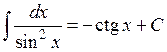 ,
, 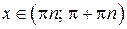 ,
, 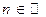 .
.
10.  ,
, 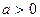 ,
, 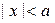 .
.
11.  ,
,  .
.
12.  ,
,  ,
,  ,
,
 .
.
13. 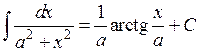 ,
,  .
.
14. 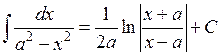 ,
,  ,
,  ,
,
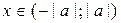 ,
,  .
.
15. 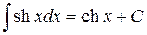 .
.
16.  .
.
|
|
|
17. 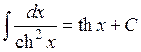 .
.
18.  ,
, 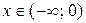 ,
, 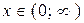 .
.
Замечание. Константа C в формулах может быть разной на каждом из интервалов, на которых определена формула.
Доказательство формул для неопределенного интеграла состоит в проверке того факта, что производная правой части равна подынтегральной функции.
Докажем для примера формулу 12 для 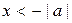 :
:

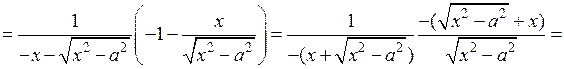
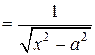 .
.
Приложение. Определения и факты, использованные при ответе на вопрос.
Определение. Производной 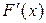 функции
функции 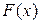 в точке x называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
в точке x называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
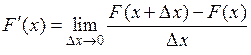 .
.
Определение (предела функции в точке):
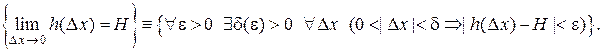
Теорема Лагранжа. Пусть функция 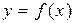 непрерывна на отрезке
непрерывна на отрезке  и дифференцируема на интервале
и дифференцируема на интервале 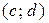 . Тогда существует такая точка
. Тогда существует такая точка  , для которой выполняется равенство
, для которой выполняется равенство
 .
.
Определение. Функция 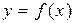 называется непрерывной на отрезке
называется непрерывной на отрезке  , если она непрерывна во всех точках интервала
, если она непрерывна во всех точках интервала 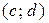 , непрерывна слева в точке
, непрерывна слева в точке 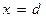 , непрерывна справа в точке
, непрерывна справа в точке  .
.
Определение. Функция 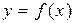 называется непрерывной в точке
называется непрерывной в точке 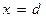 слева, если
слева, если 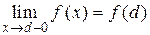 .
.
Определение (левостороннего предела функции):
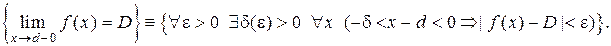
Определение. Функция 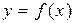 называется дифференцируемой в точке x, если приращение функции в этой точке
называется дифференцируемой в точке x, если приращение функции в этой точке 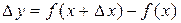 представимо в виде
представимо в виде 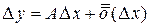 ,
, 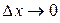 , где величина A не зависит от
, где величина A не зависит от  . При этом, слагаемое
. При этом, слагаемое 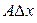 называется дифференциалом функции
называется дифференциалом функции 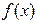 в точке x и обозначается символом
в точке x и обозначается символом 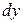 .
.
|
|
|
Определение. Функция  ,
, 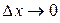 , если она представима в виде
, если она представима в виде 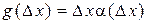 , где
, где  .
.
Теорема (о связи производной функции и дифференцируемости функции). Функция 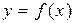 является дифференцируемой в точке x тогда и только тогда, когда у функции
является дифференцируемой в точке x тогда и только тогда, когда у функции 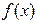 есть производная в этой точке. При этом величина A из определения дифференцируемости равна производной:
есть производная в этой точке. При этом величина A из определения дифференцируемости равна производной: 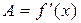 .
.
Теорема (о связи дифференцируемости и непрерывности функции). Если функция 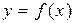 дифференцируема в точке x , то функция
дифференцируема в точке x , то функция 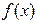 непрерывна в этой точке.
непрерывна в этой точке.
Определение. Функция 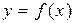 называется непрерывной в точке
называется непрерывной в точке 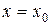 , если
, если 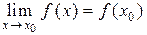 .
.
Замена переменной в неопределенном интеграле.
Теорема. Пусть функция  дифференцируема на некотором интервале
дифференцируема на некотором интервале  и пусть
и пусть 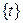 –– множество значений этой функции. Пусть для функции
–– множество значений этой функции. Пусть для функции 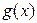 на множестве
на множестве 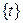 существует первообразная
существует первообразная 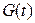 , т.е.
, т.е.
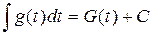 . (1)
. (1)
Тогда на интервале  для функции
для функции 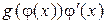 существует первообразная, равная
существует первообразная, равная 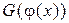 , т.е.
, т.е.
 . (2)
. (2)
Доказательство. Для доказательства формулы (2) нужно установить, что производная правой части равна подынтегральной функции
|
|
|
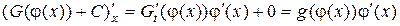 .
.
При дифференцировании было использовано правило дифференцирования сложной функции и условие теоремы (1).
Замечание. Множество  , указанное в теореме может быть интервалом, отрезком и т.д.
, указанное в теореме может быть интервалом, отрезком и т.д.
Теорема доказана.
Приложение. Определения и факты, использованные при ответе на вопрос.
Определение. Функция 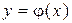 называется дифференцируемой в точке x, если приращение функции в этой точке
называется дифференцируемой в точке x, если приращение функции в этой точке 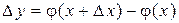 представимо в виде
представимо в виде 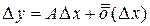 ,
, 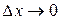 , где величина A не зависит от
, где величина A не зависит от  .
.
Определение. Функция 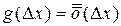 ,
, 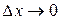 , если она представима в виде
, если она представима в виде 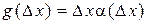 , где
, где 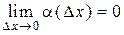 .
.
Определение (предела функции в точке):

Определение. Производной 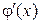 функции
функции 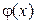 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
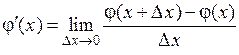 .
.
Теорема (о связи производной функции и дифференцируемости функции). Функция 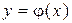 дифференцируема в точке x тогда и только тогда, когда у функции
дифференцируема в точке x тогда и только тогда, когда у функции 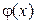 есть производная в этой точке. При этом величина A из определения дифференцируемости равна производной:
есть производная в этой точке. При этом величина A из определения дифференцируемости равна производной: 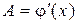 .
.
Определение. Функция 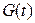 называется первообразной для функции
называется первообразной для функции 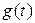 на интервале
на интервале  (на отрезке, полуинтервале и т.д.), если для всех точек t из
(на отрезке, полуинтервале и т.д.), если для всех точек t из 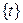 выполняется равенство
выполняется равенство 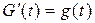 .
.
Определение. Неопределенным интегралом от функции 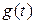 на интервале
на интервале  называется множество всех первообразных этой функции:
называется множество всех первообразных этой функции: 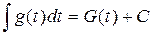 .
.
Теорема (о производной сложной функции). Пусть функция  имеет производную в точке
имеет производную в точке  , а функция
, а функция  имеет производную в точке
имеет производную в точке  . Тогда сложная функция
. Тогда сложная функция 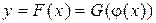 имеет производную в точке
имеет производную в точке 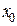 и справедливо равенство
и справедливо равенство
 .
.
Задача . Вычислить 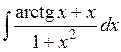 .
.
Решение. Используем линейное свойство неопределенного интеграла и замены переменной:
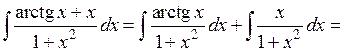

 .
.
Приложение. Определения и факты, использованные при решении задачи.
Определение. Пусть функция 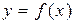 определена на интервале
определена на интервале  . Неопределенным интегралом от функции
. Неопределенным интегралом от функции 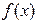 на интервале
на интервале  называется множество всех первообразных функции
называется множество всех первообразных функции 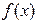 на этом интервале.
на этом интервале.
Определение. Функция  называется первообразной функции
называется первообразной функции 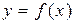 на интервале
на интервале  , если для всех
, если для всех  выполняется равенство
выполняется равенство 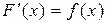 .
.
Определение. Производной функции  в точке x называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
в точке x называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
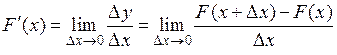 .
.
Теорема (линейное свойство неопределенного интеграла). Пусть функции 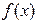 и
и  имеют первообразные на интервале
имеют первообразные на интервале  . Тогда функция
. Тогда функция 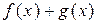 тоже имеет первообразную на
тоже имеет первообразную на  и справедлива формула
и справедлива формула
 .
.
Теорема. Пусть функция  имеет производную на некотором интервале
имеет производную на некотором интервале  и пусть
и пусть  –– множество значений этой функции. Пусть для функции
–– множество значений этой функции. Пусть для функции 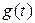 на множестве
на множестве  существует первообразная
существует первообразная 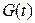 , т.е.
, т.е.  . Тогда на интервале
. Тогда на интервале  для функции
для функции 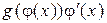 существует первообразная, равная
существует первообразная, равная 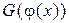 , т.е.
, т.е. 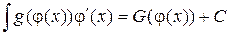 .
.
Теорема (таблица производных):
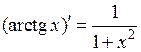 ,
, 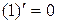 ,
,  .
.
Теорема (таблица неопределенных интегралов):
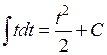 ,
, 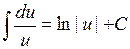 .
.
Интегрирование по частям в неопределенном интеграле.
Теорема. Пусть функции 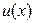 и
и 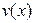 дифференцируемы на интервале
дифференцируемы на интервале 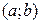 и пусть, кроме того, на этом интервале существует первообразная функции
и пусть, кроме того, на этом интервале существует первообразная функции 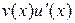 . Тогда на интервале
. Тогда на интервале  существует первообразная функции
существует первообразная функции  и справедлива формула
и справедлива формула
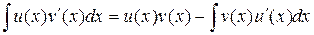 .
.
Эта формула называется формулой интегрирования по частям.
Доказательство. Запишем формулу для производной произведения:
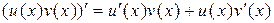 .
.
Интеграл от производной 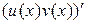 существует по определению неопределенного интеграла:
существует по определению неопределенного интеграла:
 . (1)
. (1)
Интеграл 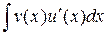 существует по условию теоремы. Следовательно, по линейному свойству интеграла, существует интеграл от функции
существует по условию теоремы. Следовательно, по линейному свойству интеграла, существует интеграл от функции  и
и
 .
.
Константу C из формулы (1) писать не нужно, так как в правой части формулы стоит неопределенный интеграл.
Теорема доказана.
Приложение. Определения и факты, использованные при ответе на вопрос.
Определение. Функция 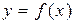 называется дифференцируемой в точке x, если приращение функции в этой точке
называется дифференцируемой в точке x, если приращение функции в этой точке  представимо в виде
представимо в виде  ,
, 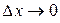 , где величина A не зависит от
, где величина A не зависит от  .
.
Определение. Функция 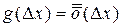 ,
, 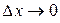 , если она представима в виде
, если она представима в виде 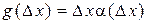 , где
, где 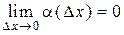 .
.
Определение (предела функции в точке):

Определение. Производной  функции
функции 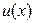 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
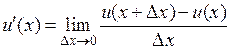 .
.
Теорема (о связи производной функции и дифференцируемости функции). Функция 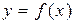 является дифференцируемой в точке x тогда и только тогда, когда у функции
является дифференцируемой в точке x тогда и только тогда, когда у функции 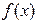 есть производная в этой точке. При этом величина A из определения дифференцируемости равна производной:
есть производная в этой точке. При этом величина A из определения дифференцируемости равна производной: 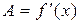 .
.
Теорема (о производной произведения). Пусть функции 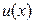 и
и 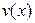 дифференцируемы в точке x . Тогда функция
дифференцируемы в точке x . Тогда функция 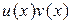 тоже дифференцируема в точке x и справедлива формула
тоже дифференцируема в точке x и справедлива формула
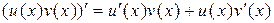 .
.
Определение. Неопределенным интегралом от функции 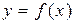 на интервале
на интервале  называется множество всех первообразных этой функции:
называется множество всех первообразных этой функции: 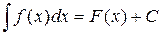 .
.
Определение. Функция 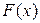 называется первообразной функции
называется первообразной функции  на интервале
на интервале  , если для всех x из
, если для всех x из  выполняется равенство
выполняется равенство 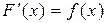 .
.
Теорема (линейное свойство интеграла). Пусть на интервале 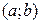 у функций
у функций 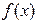 и
и  есть первообразные. Тогда функция
есть первообразные. Тогда функция 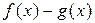 имеет на
имеет на 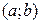 первообразную и справедлива формула
первообразную и справедлива формула
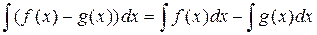 .
.
Вопрос 20. Определенный интеграл, его свойства. Площадь криволинейной трапеции.
Пусть функция 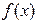 задана на отрезке
задана на отрезке  .
.
Рассмотрим разбиение отрезка  точками
точками 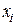 :
: 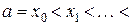
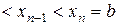 –– на n меньших сегментов. Пусть
–– на n меньших сегментов. Пусть 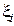 –– какая-нибудь точка i-го отрезка
–– какая-нибудь точка i-го отрезка 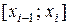 .
.
Введем обозначения: 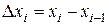 ,
, 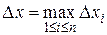 (длины частичных отрезков и максимальная длина частичных отрезков).
(длины частичных отрезков и максимальная длина частичных отрезков).
Определение 1. Число 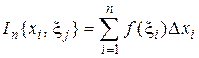 называется интегральной суммой функции
называется интегральной суммой функции 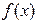 , соответствующей данному разбиению
, соответствующей данному разбиению 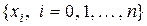 отрезка
отрезка  и данному выбору точек
и данному выбору точек 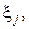
 .
.
Определение 2. Число I называется пределом интегральных сумм 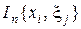 при
при 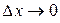 , если для произвольного
, если для произвольного 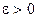 существует такое
существует такое 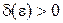 , что для всех
, что для всех 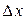 , удовлетворяющих неравенству
, удовлетворяющих неравенству 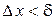 , выполняется неравенство:
, выполняется неравенство: 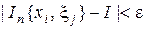 .
.
Для обозначения предела интегральных сумм используется обозначение 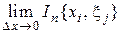 .
.
Повторим определение 2, используя символы математической логики:
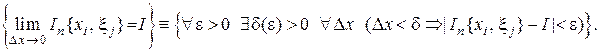
Определение 3. Функция 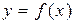 называется интегрируемой на отрезке
называется интегрируемой на отрезке  , если существует конечный предел I интегральных сумм этой функции при
, если существует конечный предел I интегральных сумм этой функции при 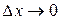 .
.
Этот предел называется определенным интегралом от функции  на отрезке
на отрезке  и обозначается следующим образом
и обозначается следующим образом
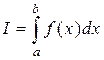
Объединяя все три определения, получаем
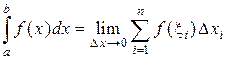 .
.
Свойства определенного интеграла.
1. 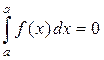 .
.
2. Если  , то
, то 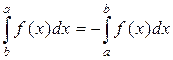 .
.
Свойства 1, 2 можно понимать как соглашение.
3. Если функция  интегрируема на
интегрируема на  , то
, то  ограничена на
ограничена на 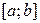 .
.
Доказательство. Предположим противное. Пусть  не ограничена на
не ограничена на  . Тогда при любом разбиении найдется такой отрезок
. Тогда при любом разбиении найдется такой отрезок 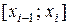 , на котором функция
, на котором функция  не ограничена. Следовательно, за счет выбора
не ограничена. Следовательно, за счет выбора  интегральная сумма
интегральная сумма  может быть сделана как угодно большой по модулю. Стало быть
может быть сделана как угодно большой по модулю. Стало быть  не может иметь конечного предела. Но тогда
не может иметь конечного предела. Но тогда  не является интегрируемой функцией, что противоречит условию.
не является интегрируемой функцией, что противоречит условию.
Свойство 3 доказано.
4. Пусть функции  и
и 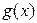 интегрируемы на
интегрируемы на  . Тогда функция
. Тогда функция 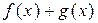 тоже интегрируема на
тоже интегрируема на  и справедлива формула
и справедлива формула
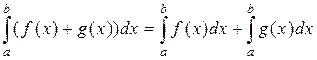 . (1)
. (1)
Доказательство. При любом разбиении отрезка  и любом выборе точек
и любом выборе точек 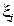 справедливо соотношение
справедливо соотношение
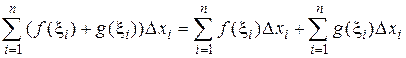 . (2)
. (2)
Так как по условию функции  и
и 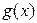 интегрируемы, то предел каждого слагаемого в правой части формулы (2) существует. Отсюда, по свойству предела (предел суммы равен сумме пределов), существует предел и левой части формулы (2). Поэтому функция
интегрируемы, то предел каждого слагаемого в правой части формулы (2) существует. Отсюда, по свойству предела (предел суммы равен сумме пределов), существует предел и левой части формулы (2). Поэтому функция 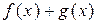 интегрируема и справедлива формула (1).
интегрируема и справедлива формула (1).
Свойство 4 доказано.
5. Если функция  интегрируема на
интегрируема на  и C –– число, то функция
и C –– число, то функция  интегрируема на
интегрируема на  и справедливо равенство
и справедливо равенство
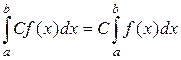 .
.
6. Если функции  ,
, 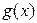 интегрируемы на
интегрируемы на  , то функция
, то функция  тоже интегрируема на
тоже интегрируема на  .
.
7. Если функция  интегрируема на
интегрируема на  , то эта функция интегрируема на любом отрезке
, то эта функция интегрируема на любом отрезке 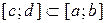 .
.
8. Пусть функция  интегрируема на отрезках
интегрируема на отрезках 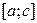 и
и 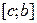 . Тогда эта функция интегрируема на отрезке
. Тогда эта функция интегрируема на отрезке  и справедливо равенство
и справедливо равенство
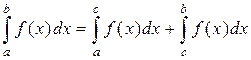 .
.
Рассмотрим фигуру, ограниченную графиком функции 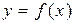 ,
,  , где
, где  –– непрерывная функция и
–– непрерывная функция и 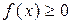 , а также отрезком
, а также отрезком 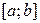 оси Ox и отрезками прямых
оси Ox и отрезками прямых 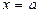 ,
, 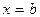 (см. рис. 8). Эта фигура называется криволинейной трапецией.
(см. рис. 8). Эта фигура называется криволинейной трапецией.
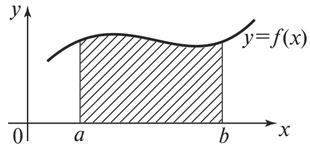
Рис. 8. Криволинейная трапеция
Введем определение площади криволинейной трапеции.
Разобьем отрезок 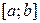 на несколько частей точками
на несколько частей точками  :
:  . В каждом отрезке
. В каждом отрезке 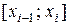 выберем точку
выберем точку  . Введем обозначение
. Введем обозначение 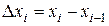 ,
, 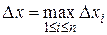 . Рассмотрим ступенчатую фигуру, состоящую из прямоугольников с основаниями
. Рассмотрим ступенчатую фигуру, состоящую из прямоугольников с основаниями 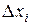 и высотами
и высотами  . Площадь
. Площадь 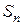 этой ступенчатой фигуры вычисляется по формуле
этой ступенчатой фигуры вычисляется по формуле
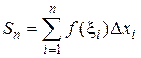 .
.
Чем меньше отрезки 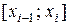 , тем лучше аппроксимирует ступенчатая фигура криволинейную трапецию. Поэтому площадью криволинейной трапеции S называется предел площадей ступенчатых фигур при стремлении к нулю длин отрезков разбиения
, тем лучше аппроксимирует ступенчатая фигура криволинейную трапецию. Поэтому площадью криволинейной трапеции S называется предел площадей ступенчатых фигур при стремлении к нулю длин отрезков разбиения
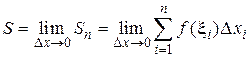 .
.
Сравнивая определение площади и определение интеграла, получаем формулу для вычисления площади криволинейной трапеции:
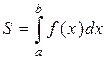 .
.
Приложение. Определения и факты, использованные при ответе на вопрос.
Определение. Функция 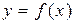 называется ограниченной на отрезке
называется ограниченной на отрезке  , если существует такое число M, что для всех
, если существует такое число M, что для всех  выполняется неравенство:
выполняется неравенство:  .
.
Определение. Функция 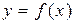 называется неограниченной на отрезке
называется неограниченной на отрезке 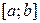 , если для любого числа M найдется такое
, если для любого числа M найдется такое  , что
, что 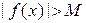 .
.
Теорема (о пределе суммы). Пусть 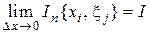 ,
,  . Тогда
. Тогда 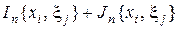 имеет предел при
имеет предел при 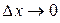 и справедливо равенство
и справедливо равенство
 .
.
Дата добавления: 2020-11-29; просмотров: 69; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
