Дифференцирование неявно заданных функций
Тема Дифференциальное исчисление функции одной переменной
ЛЕКЦИЯ 1. Определение производной. Правила дифференцирования .
Пусть задана некоторая функция y = f (x). Выберем в области определения функции два произвольных значения аргумента х их1. Обозначим за Dх разность между двумя значениями аргумента Dх = х1 – х, (т.е х1 = х +Dх).
Замечание. Dхможет быть как больше нуля, если х1 > х, так именьше нуля, если х1 < х.
Вычислим значения функции в этих точках y = f(x) и y 1= f(x1).
Приращением функции Df (x) называется разность между двумя значениями функции Df(x) = f(x1) - f(x) = y 1 – y или Df(x) = f(х + Dx) – f(x).
Если при Dх® 0 существует конечный предел отношения приращения функции к вызвавшему его приращению аргумента, то функция f(x) называется дифференцируемой в точке х, а значение предела называется производной от функции f(x) в точке х и обозначается
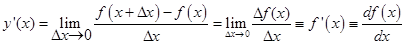
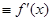 (1.1)
(1.1)
Производная – это функция от того же аргумента, что и f(x). Операция вычисления производной называется дифференцированием функции.
Геометрический смысл производной. Если изобразить на рисунке график функции f(x), отметить точки х и х1 = х + Dх, то МС = Dх, NC = Df(x). Величина отношения
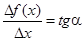 (1.2)
(1.2)
равна тангенсу угла наклона секущей MN к оси абсцисс (см. рис.1.1).
Если Dх ® 0, то точка N стремится по графику функции к точке M, секущая MN стремится занять положение касательной МК к графику функции f(x) в точке M, угол наклона секущей α стремится к углу наклона касательной φ. Сравнивая формулы (1.1) и (1.2) мы можем сказать, что значение производной f ¢(x) в точке х равно тангенсу угла наклона касательной к графику y = f(x) в точке М с координатами (х, f(x)).
|
|
|
Уравнение касательной в точке М
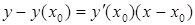 ,
,
уравнение нормали
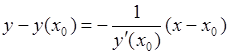 ,
,
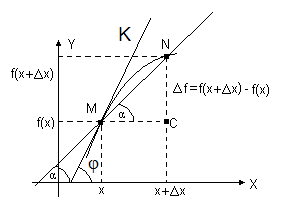
Рис. 1.1. Геометрический смысл производной
В механике производная от пути по времени есть скорость 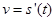 . Если функция
. Если функция 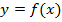 описывает какой-либо физический процесс, то производная y ’ есть скорость протекания этого процесса. В этом состоит физический смысл производной.
описывает какой-либо физический процесс, то производная y ’ есть скорость протекания этого процесса. В этом состоит физический смысл производной.
Правила дифференцирования.
На практике функции дифференцируют с помощью ряда правил и формул.
Производная постоянной С равна нулю
( C )` = 0 (1.3)
Производная линейной комбинации функций f1 (x) и f2(x)
у(х) = с1f1(x)+c2f2(x), (1.4)
где с1 и c2 произвольные постоянные, равна линейной комбинации производных
|
|
|
у ¢(x) = (с1f1(x)+c2f2(x))¢ = с1f1 ¢ (x)+c2f2 ¢ (x). (1.5)
Следствие. Постоянный множитель С можно вынести за знак производной
(С у (x)) ¢= С у ¢(x).
Производная произведения функций у(x) =f(x) 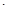 g(x) вычисляется по правилу: произведение производной от первой функции на неизменную вторую плюс произведение производной от второй функции на неизменную первую
g(x) вычисляется по правилу: произведение производной от первой функции на неизменную вторую плюс произведение производной от второй функции на неизменную первую
у (x)’ = (f(x)g(x))¢ = f ¢(x)·ּg(x) + f(x)·ּg ¢(x). (1.6)
Правило можно обобщить на случай производной произведения n функций
(f1(x) 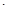 f2(x)
f2(x) 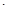 .. …. …
.. …. … 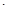 fn(x))¢ =
fn(x))¢ =
= f1(x)¢ 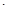 f2(x)
f2(x) 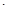 ….
…. 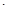 fn(x)+ f1(x)
fn(x)+ f1(x) 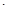 f2(x)¢
f2(x)¢ 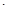 ….
…. 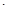 fn(x)+….+ f1(x)
fn(x)+….+ f1(x) 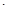 f2(x)
f2(x) 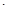 …..
….. 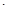 fn(x)¢
fn(x)¢
Производная частного двух функций у (x) = f(x)/g(x) вычисляется по правилу
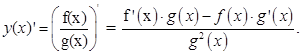
(1.7)
Таблица производных основных элементарных функций
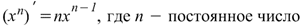 Производная степенной функции Производная степенной функции
| 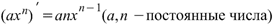 Производная степенной функции Производная степенной функции
|
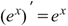 Производная экспоненциальной функции Производная экспоненциальной функции
| 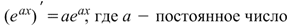 Производная экспоненты Производная экспоненты
|
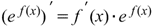 Производная сложной экспоненциальной функции Производная сложной экспоненциальной функции
| 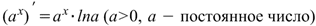 Производная экспоненциальной функции Производная экспоненциальной функции
|
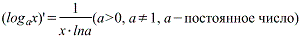 Производная логарифмической функции Производная логарифмической функции
| 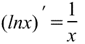 Производная натурального логарифма Производная натурального логарифма
|
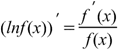 Производная натурального логарифма функции
Производная натурального логарифма функции
| |
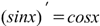 Производная синуса Производная синуса
| 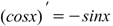 Производная косинуса Производная косинуса
|
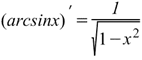 Производная арксинуса Производная арксинуса
| 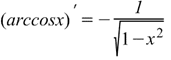 Производная арккосинуса Производная арккосинуса
|
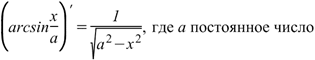 Производная арксинуса Производная арксинуса
|
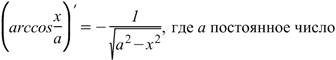 Производная арккосинуса Производная арккосинуса
|
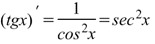 Производная тангенса Производная тангенса
| 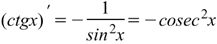 Производная котангенса Производная котангенса
|
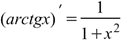 Производная арктангенса Производная арктангенса
| 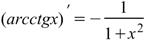 Производная арккотангенса Производная арккотангенса
|
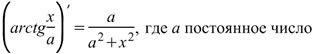 Производная арктангенса Производная арктангенса
| 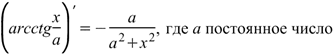 Производная арккотангенса Производная арккотангенса
|
|
|
|
Примеры.
1. (6 sin x - 2 ln x)¢ = (6 sin x)¢ - (2 ln x)¢ = 6 (sin x)¢ - 2 (ln x)¢ = 6 cos x - 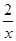
2. (lnx∙cosx)' = 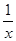 ∙cosx - lnx∙sinx
∙cosx - lnx∙sinx
3. 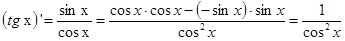
Правила дифференцирования
| Производная произведения (функции) на постоянную: | 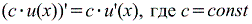
|
| Производная суммы (функций): | 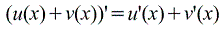
|
| Производная произведения (функций): | 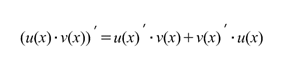
|
| Производная частного (функций): | 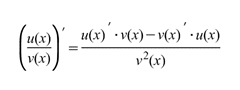
|
| Производная сложной функции: | 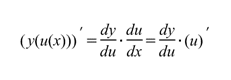
|
Дифференцирование сложной функции. Пусть дифференцируемая функция g(x) является аргументами другой функции f(x). В этом случае говорят о сложной функции у(x) = f(g(x)) или суперпозиции функций f и g.
Вычислим производную сложной функции. Найдем приращение функции Dу(x). Для этого выберем в области определения функции два произвольных значения аргумента х их1 = x + Dx. Вычислим соответствующие значения функции g (x + Dx) и g (x) и найдем ее приращение
D g (x) = g (x + Dx) - g (x) 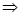 g (x + Dx) = g (x) + Dg (x).
g (x + Dx) = g (x) + Dg (x).
|
|
|
Аналогично найдем значения функции f (g (x + Dx)) и f (g (x)). Тогда
Df = f (g(x+Dx)) – f (g(x)) = f (g (x) + Dg (x)) – f (g(x)). (1.8)
Подставим выражение (1.8) в (1.1). Умножим и разделим на D g (x) и сгруппируем сомножители. Тогда производная сложной функции
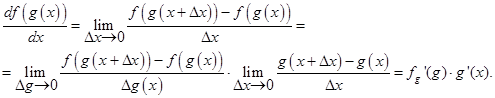 (1.9)
(1.9)
В компактной форме производную от сложной функции можно записать так
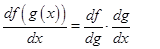 (1.10)
(1.10)
Иначе, для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.
Пример. у = ln (sin(x2)). Эта сложная функция состоит из следующих отдельных функций: f = ln g, g = sin h, h = x2. При этом
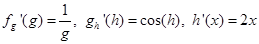
Тогда 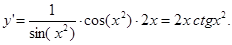
Пример. Пользуясь формулами дифференцирования, найти производные следующих функций:
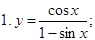
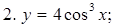
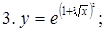
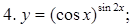
Решение.
1. 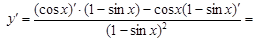
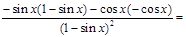
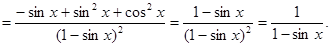
2. 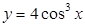 есть сложная функция
есть сложная функция 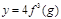 , где
, где 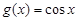 .
.
Производная сложной функции имеет вид 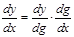 . Следовательно,
. Следовательно,
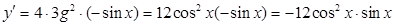 .
.
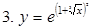 - сложная функция
- сложная функция 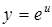 , где
, где 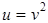 , а
, а 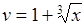 ,
,
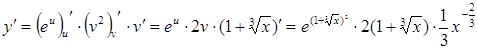 .
.
Дифференцирование неявно заданных функций
Если функция задана уравнением 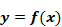 , разрешенным относительно y, то функция задана в явном виде (явная функция).
, разрешенным относительно y, то функция задана в явном виде (явная функция).
Под неявным заданием функции понимают задание функции в виде уравнения 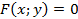 , не разрешенного относительно y.
, не разрешенного относительно y.
Всякую явно заданную функцию 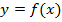 можно записать как неявно заданную уравнением
можно записать как неявно заданную уравнением 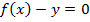 , но не наоборот.
, но не наоборот.
Не всегда легко, а иногда и невозможно разрешить уравнение относительно y.
Если неявная функция задана уравнением 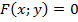 , то для нахождения производной от y по x нет необходимости разрешать уравнение относительно y: достаточно продифференцировать это уравнение по x , рассматривая при этом y как функцию x, и полученное затем уравнение разрешить относительно y ’.
, то для нахождения производной от y по x нет необходимости разрешать уравнение относительно y: достаточно продифференцировать это уравнение по x , рассматривая при этом y как функцию x, и полученное затем уравнение разрешить относительно y ’.
Производная неявной функции выражается через аргумент x и функцию y.
Пример. Найти производную функции y, заданную уравнением 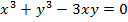 .
.
Решение. Функция y задана неявно. Дифференцируем по x наше равенство.
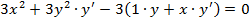 .
.
Из полученного соотношения следует, что 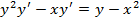 , то есть
, то есть 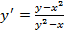 .
.
Дата добавления: 2020-11-29; просмотров: 109; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
