Выполните задание самостоятельно
ОУД.04 Математика (2 пары) группа ПС-11 18.11.2020
Рекомендации:
- не забывайте изучать Тему 9 по инструкции от 02.11.2020;
- каждая следующая тема содержит в себе материал из ранее изученных тем, поэтому смотрите и повторяйте предыдущий материал;
- в обеих тетрадях ставим на полях дату занятия по расписанию.
Тема 9 Обратные тригонометрические функции
Арксинус
Рассмотрим график функции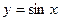 
на отрезке 
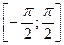. На этом отрезке функция возрастает и принимает все значения от -1 до 1.
Следовательно, при любом значении 
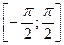на отрезке , уравнение 
имеет только один корень 
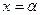, где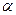 
называется арксинусом числа 
и обозначается так: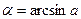 
.
Иными словами арксинус – это угол 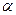, синус которого равен 
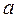. Значения 
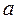находим в таблице значений тригонометрических функций в строке 
, а выше по столбцу напротив значения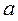 
определяем угол .
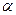Пример 1 Вычислить: а)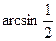 
б) 
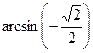
а) В таблице значений тригонометрических функций в строке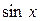 
находим самое первое от нуля число 
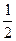и определяем угол (сверху).
Решение: 
= 
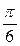
б) Сначала учитываем нечётность 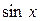и минус выносим вперёд, затем в таблице значений тригонометрических функций в строке 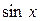находим самое первое от нуля число 
и определяем угол.
Решение: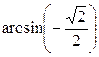 
= 
= 
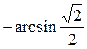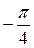
Выполните задание самостоятельно
№1. Вычислите: а)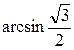 
; б) 
; в)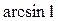 
+ 
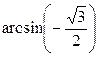
Арккосинус
Рассмотрим график функции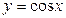 
на отрезке 
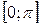. На этом отрезке функция убывает и принимает все значения от -1 до 1.
|
|
|
Следовательно, при любом значении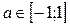 
на отрезке 
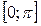, уравнение 
имеет только один корень 
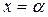, где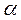 
называется арккосинусом числа 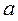и обозначается так: 
.
Иными словами арккосинус – это угол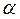 
, косинус которого равен 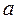. Значения 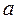находим в таблице значений тригонометрических функций в строке 
, а выше по столбцу напротив 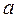определяем угол .
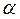Пример 2 Вычислить: а)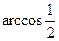 
б) 
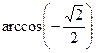
а) В таблице значений тригонометрических функций в строке 
находим самое первое от нуля число 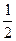и определяем угол (сверху).
Решение: 
= 
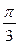
б) Сначала отрицательное значение 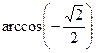заменяем на 
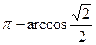, затем в таблице значений тригонометрических функций в строке находим самое первое от нуля число и определяем угол.
Решение: = =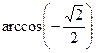 
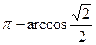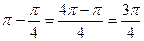
Выполните задание самостоятельно
№2. Вычислите: а) 
; б) 
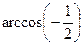; в)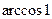 
+ 
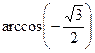
Арктангенс
Рассмотрим график функции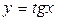 
наинтервале 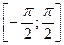. На этом промежутке функция возрастает и принимает все значения из множества действительных чисел.
Следовательно, при любом значении функции на интервале 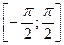имеется единственное значение 
. Число 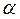называется арктангенсом числа а и обозначается 
.
|
|
|
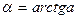Арктангенсом числа а называется такое число 
, тангенс которого равен а.
Пример 3 Вычислить а) 
; б) 
а) В таблице значений тригонометрических функций в строке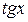 
находим самое первое от нуля число 1 и определяем угол (сверху).
Решение: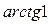 
= 
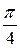
б) Сначала учитываем нечётность 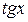и минус выносим вперёд, затем в таблице значений тригонометрических функций в строке 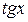находим самое первое от нуля число 
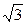и определяем угол.
Решение: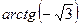 
= 
= 
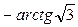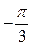
Выполните задание самостоятельно
№3. Вычислить а) 
; б)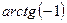 
Арккотангенс
Рассмотрим график функции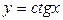 
наинтервале 
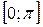. На этом промежутке функция убывает и принимает все значения из множества действительных чисел.
Следовательно, при любом значении функции на интервале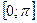 
имеется единственное значение 
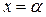. Число 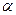называется арккотангенсом числа а и обозначается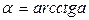 
Арккотангенсом числа а называется такое число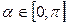 
, котангенс которого равен а.
Пример 4 Вычислить: а)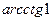 
; б) 
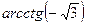
а) В таблице значений тригонометрических функций в строке 
находим самое первое от нуля число 1 и определяем угол (сверху).
Решение: =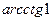 
б) Сначала учитываем нечётность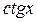 
и минус выносим вперёд, затем в таблице значений тригонометрических функций в строке 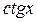находим самое первое от нуля число 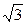и определяем угол.
|
|
|
Решение: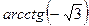 
= 
= 
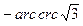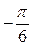
Дата добавления: 2020-11-29; просмотров: 68; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!