Примеры решения неравенств методом интервалов
Теперь можно собрать воедино всю представленную информацию, достаточную для решения неравенств методом интервалов, и разобрать решения нескольких примеров.
Пример.
Решите неравенство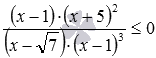 
.
Решение.
Проведем решение этого неравенства методом интервалов. Очевидно, нули числителя это 1 и −5, а нули знаменателя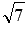 
и 1. Отмечаем их на числовой прямой, при этом точки с координатами 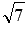и 1 выколотые как нули знаменателя, а оставшийся нуль числителя −5 изобразим обычной точкой, так как решаем нестрогое неравенство:
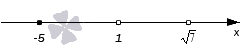
Теперь проставляем знаки на промежутках, придерживаясь правила сохранения или изменения знака при переходе через нули. Над крайним справа промежутком будет знак + (это можно проверить, вычислив значение выражения в левой части неравенства в какой-либо точке этого промежутка, например, при x=3). При переходе через 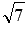знак изменяем, при переходе через 1 – оставляем таким же, и при переходе через −5 опять оставляем знак без изменения:
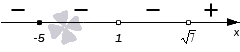
Так как мы решаем неравенство со знаком ≤, то осталось изобразить штриховку над промежутками, отмеченными знаком −, и по полученному изображению записать ответ.
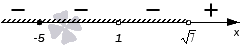
Итак, искомое решение таково: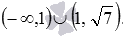 
.
Ответ:
.
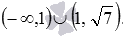Справедливости ради обратим внимание на то, что в подавляющем большинстве случаев при решении рациональных неравенств их предварительно приходится преобразовывать к нужному виду, чтобы стало возможным их решение методом интервалов. Как проводить такие преобразования мы подробно обсудим в статье решение рациональных неравенств, а сейчас приведем пример, иллюстрирующий один важный момент, касающийся квадратных трехчленов в записи неравенств.
|
|
|
Пример.
Найдите решение неравенства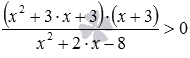 
.
Решение.
С первого взгляда на данное неравенство кажется, что его вид подходит для применения метода интервалов. Но не помешает проверить, действительно ли дискриминанты квадратных трехчленов в его записи отрицательны. Вычислим их для успокоения совести. Для трехчлена x2+3·x+3 имеем D=32−4·1·3=−3<0, а для трехчлена x2+2·x−8 получаем D’=12−1·(−8)=9>0. Это означает, что для придания этому неравенству нужного вида требуются преобразования. В данном случае достаточно трехчлен x2+2·x−8 представить как (x+4)·(x−2), и дальше решать методом интервалов неравенство 
.
Ответ:
.
Обобщенный метод интервалов
Обобщенный метод интервалов позволяет решать неравенства вида f(x)<0 (≤, >, ≥), где f(x) – произвольное выражение с одной переменной x. Запишем алгоритм решения неравенств обобщенным методом интервалов:
· Сначала надо найти область определения функции f и нули этой функции.
|
|
|
· На числовой прямой отмечаются граничные, в том числе и отдельные точки области определения. Например, если областью определения функции служит множество (−5, 1] ∪ {3} ∪ [4, 7) ∪ {10}, то мы отметим точки с координатами −5, 1, 3, 4, 7 и 10, причем точки с координатами −5 и 7 сделаем выколотыми, а остальные - сплошными. Для удобства будем их изображать цветными, например, оранжевыми, чтобы в дальнейшем не путать с нулями функции.
· Дальше на числовую прямую переносятся нули функции. Они изображаются выколотыми точками при решении строгих неравенств, а при решении нестрогих неравенств – обыкновенными точками. Возможны случаи, когда нули функции будут совпадать с граничными и/или отдельными точками области определения. При этом точки из цветного перекрашиваются в основной черный цвет и при решении строгих неравенств делаются выколотыми. Нули разбивают область определения функции на промежутки.
· Определяются знаки на каждом промежутке области определения, в основном путем вычисления значения функции f в какой-либо одной точке из каждого промежутка, а также знаки функции во всех отдельных точках (при их наличии).
· Дальше наносится штриховка. Если решается неравенство со знаком < или ≤, то наносится штриховка над промежутками со знаком −, а если решается неравенство со знаком > или ≥, то над промежутками со знаком +.
|
|
|
· Наконец, записывается ответ. Им будет числовое множество, включающее в себя
o все промежутки со штриховкой
o все отдельные точки области определения со знаком +, если знак решаемого неравенства > или ≥, со знаком −, если знак решаемого неравенства < или ≤.
Понятно, что алгоритм, приведенный в начале статьи, является частным случаем этого алгоритма. В нем нахождение нулей знаменателя по сути является нахождением области определения функции, соответствующей левой части неравенства.
Покажем применение обобщенного метода интервалов на практике.
Пример.
Решите неравенство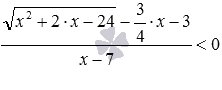 
.
Решение.
Вводим функцию f такую, что 
. Сначала нужно найти область определения функции f:
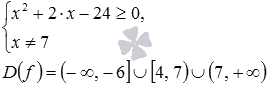
Также нам нужны нули этой функции. Для их нахождения проводим решение иррационального уравнения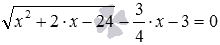 
, находим единственный корень x=12.
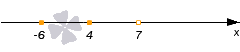
Отмечаем оранжевым цветом на числовой прямой граничные точки области определения, сплошными делаем точки с координатами −6 и 4, а точку с координатой 7 делаем выколотой. Отдельных точек область определения не имеет. Вот что мы получаем:
|
|
|
Теперь на числовую прямую добавляем нуль функции, отмечаем его выколотой точкой, так как решаем строгое неравенство. (Если бы нуль функции совпал с граничной точкой −6 или 4, то мы бы ее из сплошной оранжевой сделали выколотой черной, с семеркой нуль совпасть, естественно, не мог бы, так как в ней функция не определена). Имеем:
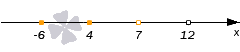
Теперь нам надо определить знаки на четырех промежутках (12, +∞), (7, 12), [4, 7) и (−∞, −6] (на интервале (−6, 4) знак не определяем, так как он не является частью области определения функции). Для этого возьмем по одной точке из каждого промежутка, например, 16, 8, 6 и −8, и вычислим в них значение функции f:
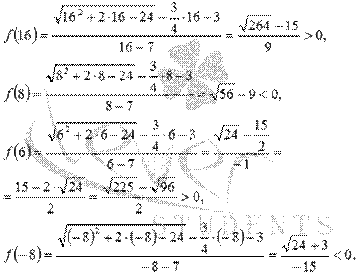
Если возникли вопросы как было выяснено, какими являются вычисленные значения функции, положительными или отрицательными, то изучите материал статьи сравнение чисел.
Расставляем только что определенные знаки, и наносим штриховку над промежутками со знаком минус:
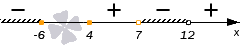
В ответ записываем объединение двух промежутков со знаком −, имеем (−∞, −6] ∪ (7, 12). Обратите внимание, что −6 включено в ответ (соответствующая точка сплошная, а не выколотая). Дело в том, что это не нуль функции (который при решении строгого неравенства мы бы не включили в ответ), а граничная точка области определения (она цветная, а не черная), при этом входящая в область определения. Значение функции в этой точке отрицательно (о чем свидетельствует знак минус над соответствующим промежутком), то есть, она удовлетворяет неравенству. А вот 4 включать в ответ не нужно (как и весь промежуток [4, 7)), несмотря на то, что она изображена сплошной. Почему? Да потому что в ней, как и на веем промежутке [4, 7), значения функции положительны (о чем свидетельствует знак плюс над ним), а это не удовлетворяет решаемому неравенству.
Итак, невыколотые цветные точки включаются в ответ в двух случаях:
· если они являются частью промежутка со штриховкой,
· если они являются отдельными точками области определения функции, значения функции в которых удовлетворяют решаемому неравенству.
Ответ:
(−∞, −6] ∪ (7, 12).
Дата добавления: 2020-11-27; просмотров: 96; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!