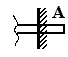Методические указания к решению задач статики.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО СТАТИКЕ
Основные понятия и определения статики
Плоская произвольная система сил - система сил, как угодно расположенных, в одной плоскости.
Для равновесия любой системы сил необходимо и достаточно, чтобы главный вектор 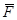 этой системы сил и ее главный момент
этой системы сил и ее главный момент 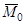 относительно любого центра О были равны нулю, то есть чтобы выполнялись условия
относительно любого центра О были равны нулю, то есть чтобы выполнялись условия
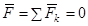 ,
,  (1)
(1)
Из (1) вытекают три аналитических условия (уравнения) равновесия плоской произвольной системы сил, которые можно записать в трех различных формах.
Первая (основная) форма условий равновесия:
для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из координатных осей 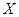 и
и  и алгебраическая сумма моментов этих сил относительно любой точки О, лежащей в плоскости действия сил, были равны нулю, то есть
и алгебраическая сумма моментов этих сил относительно любой точки О, лежащей в плоскости действия сил, были равны нулю, то есть
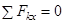 ,
,
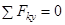 , (2)
, (2)
 .
.
Вторая форма условий равновесия:
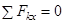 ,
,
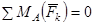 , (3)
, (3)
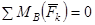 .
.
Прямая АВ не должна быть перпендикулярна оси 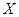 .
.
Третья форма условий равновесия:
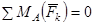 ,
,
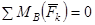 , (4)
, (4)
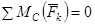 .
.
Точки А, В, С не должны лежать на одной прямой.
Проекцией силы 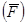 на ось
на ось 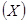 называют отрезок
называют отрезок 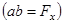 , заключенный между перпендикулярами, опущенными из начала
, заключенный между перпендикулярами, опущенными из начала 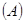 и конца
и конца 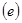 вектора силы на эту ось.
вектора силы на эту ось.
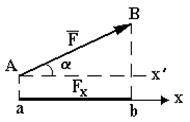
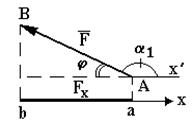
а)  b)
b) 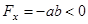
Рис. 1
Проекция силы на ось 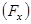 равна произведению модуля силы
равна произведению модуля силы  на косинус угла между силой
на косинус угла между силой 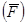 и положительным направлением оси
и положительным направлением оси 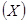 .
.
Из рис. 1 следует:
а) если этот угол  острый - проекция положительна и
острый - проекция положительна и
|
|
|
 ;
;
б) если угол 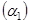 тупой - проекция отрицательна и
тупой - проекция отрицательна и
 .
.
Практика показывает, что угол 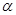 может быть (рис. 2):
может быть (рис. 2):
1) 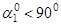
| 2) 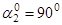
| 3) 
| 4) 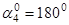
| 5) 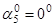
|
|
| ||||
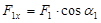
| 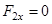
| 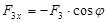
| 
| 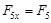
|
Рис. 2
Моментом силы 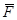 относительно любой точки О называется произведение модуля силы на плечо, взятое со знаком плюс или минус.
относительно любой точки О называется произведение модуля силы на плечо, взятое со знаком плюс или минус.
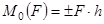
| 
|
Плюс берется, если сила стремится повернуть тело вокруг точки О против хода часовой стрелки, минус, - если, - по ходу часовой стрелки.
Плечо 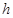 - кратчайшее расстояние от точки поворота О до линии действия силы.
- кратчайшее расстояние от точки поворота О до линии действия силы.
Если линия действия силы пересекает точку О, то ее момент относительно этой точки равен нулю, так как  .
.
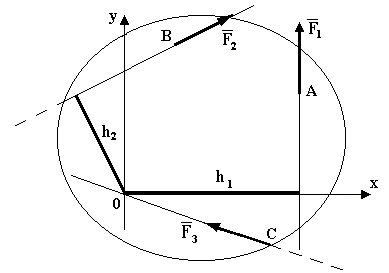
Рис. 3
Из рис. 3:

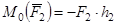
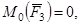 так как
так как  .
.
При определении момента силы 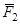 , у студента вызывает трудность вычисление плеча
, у студента вызывает трудность вычисление плеча  . Поэтому, чтобы упростить эту задачу, надо:
. Поэтому, чтобы упростить эту задачу, надо:
а) разложить силу 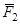 на ее составляющие
на ее составляющие 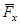 и
и 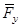 параллельно выбранным осям
параллельно выбранным осям 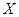 и
и  ;
;
б) применить теорему Вариньона (рис. 4)
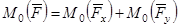 . (5)
. (5)
Момент равнодействующей силы 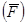 относительно точки О равен алгебраической сумме моментов составляющих ее сил
относительно точки О равен алгебраической сумме моментов составляющих ее сил 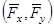 относительно той же точки О.
относительно той же точки О.

Рис. 4
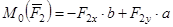 или
или
 .
.
Парой сил называют две силы 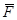 и
и 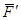 равные по величине, противоположно направленные и параллельные между собой (рис. 5).
равные по величине, противоположно направленные и параллельные между собой (рис. 5).
|
|
|
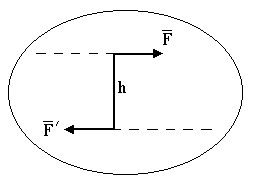
Рис. 5
Моментом пары сил называют произведение модуля одной из сил пары на плечо, взятое со знаком плюс или минус, то есть
 .
.
Момент пары считается положительным, если пара, в плоскости ее действия, стремится повернуть тело против хода часовой стрелки, и отрицательным, если, - по ходу.
Плечо пары 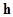 - кратчайшее расстояние между линиями действия пары.
- кратчайшее расстояние между линиями действия пары.
Так как действие пары сил на твердое тело характеризуется (определяется) только моментом, то рис.6а и рис.6b считаются идентичными
 (а)
(а)
|  (b)
(b)
|
Рис. 6
Распределенные силы - система сил распределенных вдоль поверхности по тому или иному закону.
Плоская система распределенных сил характеризуется ее интенсивностью 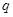 .
.
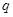 - значение силы, приходящейся на единицу длины нагруженного отрезка.
- значение силы, приходящейся на единицу длины нагруженного отрезка.
Измеряется 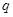 в ньютонах, деленных на метр (Н/м).
в ньютонах, деленных на метр (Н/м).
При составлении расчетной схемы распределенную нагрузку заменяют сосредоточенной силой 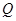 :
:
- величина силы 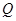 пропорциональна площади эпюры распределения сил;
пропорциональна площади эпюры распределения сил;
- направлена сила 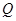 параллельно заданной нагрузке в сторону ее действия;
параллельно заданной нагрузке в сторону ее действия;
- линия действия силы 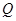 проходит через центр тяжести той же эпюры распределения сил.
проходит через центр тяжести той же эпюры распределения сил.
Силы равномерно распределенные вдоль отрезка прямой АВ (рис. 7а)
|
|
|
(например, силы тяжести, действующие на однородную балку).
| а) b) | 
|
Рис. 7
Силы распределенные вдоль отрезка прямой по линейному закону (рис. 8а)
(например, силы давления воды на пластину).

|
| а) b) |
Рис. 8
Методические указания к решению задач статики.
Решение задач статики, сводится к определению реакций опор, с помощью которых крепятся балки, жесткие рамы, всевозможные конструкции. Определение модулей и направлений сил реакций связей (опор) имеет первостепенное практическое значение, так как, зная реакции, будем знать и силы давления на связь. А это, в свою очередь, позволит, пользуясь законами сопротивления материалов, рассчитать прочность конструкции или сооружения.
Типы связей. Реакции связей
| Наименование связей и их обозначение на схемах | Реакции связей | ||||

| Реакция 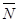 направлена к телу. Реакция направлена к телу. Реакция 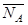 гладкой поверхности направлена по общей нормали к поверхностям соприкасающихся тел. Реакция гладкой поверхности направлена по общей нормали к поверхностям соприкасающихся тел. Реакция 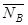 уступа направлена по нормали к поверхности опирающегося тела. уступа направлена по нормали к поверхности опирающегося тела.

| ||||
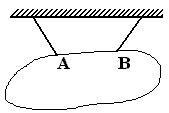
| Реакция  направлена вдоль нити от тела (нить работает только на растяжение) направлена вдоль нити от тела (нить работает только на растяжение)

| ||||
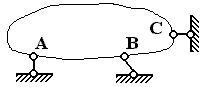
| Реакция  направлена вдоль стержня, стержень работает либо на растяжение, либо на сжатие. направлена вдоль стержня, стержень работает либо на растяжение, либо на сжатие.

| ||||
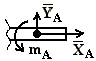
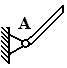
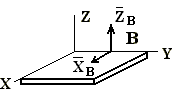
4. цилиндрический шарнир (подшипник)
А – ось подшипника перпендикулярна чертежу
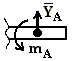
 В – ось подшипника совпадает с осью Y
В – ось подшипника совпадает с осью Y
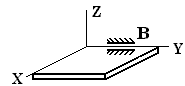
| Составляющие реакции лежат в плоскости, перпендикулярной оси шарнира.

| ||||
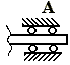
5. подвижная шарнирная опора (на катках)
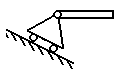
| Реакция направлена перпендикулярно опорной плоскости

| ||||
6. Заделка
| Реакции при действии на тело плоской системы сил
|
|
|
|
Порядок (план) решения задач.
Приступая к решению задания, необходимо разобраться в условии задачи и рисунке, а затем:
1. Составить расчетную схему, которая включает:
- объект равновесия,
- активные (заданные) силы,
- силы реакции, заменяющие действия отброшенных связей.
2. Определить вид полученной системы сил и выбрать, соответствующие ей, уравнения равновесия;
3. Выяснить, является ли задача статически определимой;
4. Составить уравнения равновесия и определить из них силы реакции;
5. Сделать проверку полученных результатов.
При замене связей (опор) силами реакций помнить:
- если связь препятствует перемещению тела только в одном каком-нибудь направлении, то направление ее реакции противоположно этому направлению;
- если же связь препятствует перемещению тела по многим направлениям, то силу реакции такой связи изображают ее составляющими, показывая их параллельно выбранным координатным осям 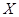 и
и 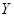 .
.
Решение уравнений равновесия будет тем проще, чем меньшее число неизвестных будет входить в каждое из них. Поэтому, при составлении уравнений равновесия следует:
1) координатные оси 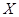 и
и 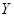 располагать так, чтобы одна из осей была перпендикулярна к линии действия хотя бы одной из неизвестных сил, в этом случае проекция неизвестной силы исключается из соответствующего уравнения равновесия;
располагать так, чтобы одна из осей была перпендикулярна к линии действия хотя бы одной из неизвестных сил, в этом случае проекция неизвестной силы исключается из соответствующего уравнения равновесия;
2) за центр моментов выбирать точку, в которой пересекаются линии действия наибольшего числа неизвестных сил реакций, тогда моменты этих сил не войдут в уравнение моментов.
Если сила 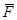 в плоскости
в плоскости 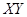 имеет две составляющие ее силы
имеет две составляющие ее силы  и
и  , то при вычислении момента силы
, то при вычислении момента силы 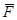 вокруг некоторой точки О, полезно применить теорему Вариньона, вычислив сумму моментов составляющих ее сил относительно этой точки (см. рис. 4).
вокруг некоторой точки О, полезно применить теорему Вариньона, вычислив сумму моментов составляющих ее сил относительно этой точки (см. рис. 4).
Если к телу в числе других сил приложена пара сил, то ее действие учитывается только в уравнении моментов сил, куда вносится момент этой пары, с соответствующим, знаком.
Система сходящихся сил
Система сил, линии действия которых пересекаются в одной точке, называется системой сходящихся сил.
Согласно аксиоме статики, равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах (рис.9).

Рис.9
Из треугольника 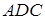 находим модуль равнодействующей по формуле
находим модуль равнодействующей по формуле
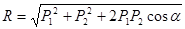 ,
,
где 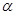 -угол между векторами
-угол между векторами  и
и 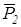 .
.
Применяя последовательно правило параллелограмма, можно найти равнодействующую скольких угодно сходящихся сил. Найдем сначала равнодействующую трех сил 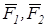 и
и 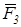 , приложенных в одной точке и не лежащих в одной плоскости (рис.10).
, приложенных в одной точке и не лежащих в одной плоскости (рис.10).
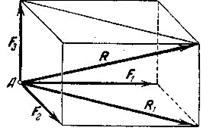
Рис.10
Сложив по правилу параллелограмма силы 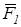 и
и 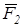 , получим их равнодействующую
, получим их равнодействующую  , а сложив затем
, а сложив затем  и
и 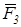 , найдем равнодействующую
, найдем равнодействующую 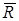 трех данных сил
трех данных сил 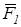 ,
, 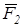 и
и 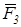 . Таким образом, равнодействующая трех сил, приложенных в одной точке и не лежащих в одной плоскости, равна по модулю и направлению диагонали параллелепипеда, построенного на этих трех силах (правило параллелепипеда). Заметим, что при нахождении равнодействующей двух сил нет надобности строить весь параллелограмм. Для этого из конца вектора первой силы
. Таким образом, равнодействующая трех сил, приложенных в одной точке и не лежащих в одной плоскости, равна по модулю и направлению диагонали параллелепипеда, построенного на этих трех силах (правило параллелепипеда). Заметим, что при нахождении равнодействующей двух сил нет надобности строить весь параллелограмм. Для этого из конца вектора первой силы 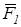 (рис.11) проводим вектор второй силы
(рис.11) проводим вектор второй силы 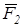 . Вектор, соединяющий начальную и конечную точки полученной ломаной линии будет представлять собой по модулю и направлению равнодействующую
. Вектор, соединяющий начальную и конечную точки полученной ломаной линии будет представлять собой по модулю и направлению равнодействующую 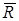 двух данных сил
двух данных сил 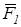 и
и 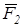 (правило треугольника).
(правило треугольника).
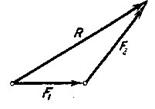
Рис.11
Как известно, в статике сила является скользящим вектором. Поэтому, точки приложения сходящихся сил можно перенести по линиям их действия в точку пересечения этих линий, а следовательно, систему сходящихся сил всегда можно заменить системой сил, приложенных в одной точке.
Пусть теперь нужно сложить несколько сил, например, четыре силы 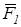 ,
, 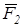 ,
, 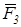 и
и 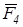 , приложенных в точке
, приложенных в точке 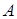 (рис.12). Применяя последовательно правило треугольника, получим ломаную линию
(рис.12). Применяя последовательно правило треугольника, получим ломаную линию 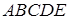 . Вектор
. Вектор 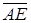 , соединяющий начальную и конечную точки ломаной линии, изображает искомую равнодействующую
, соединяющий начальную и конечную точки ломаной линии, изображает искомую равнодействующую 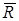 четырех сил
четырех сил 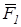 ,
, 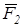 ,
, 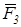 и
и 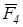 .
.
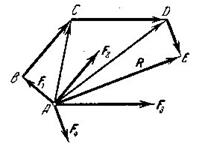
Рис.12
Таким образом, равнодействующая сходящихся сил изображается замыкающей стороной многоугольника сил, приложена в точке пересечения линий действия сил и равна их геометрической сумме
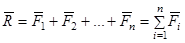 . (6)
. (6)
Спроектировав равенство (6) на координатные оси, и учитывая, что проекция суммы векторов на какую-нибудь ось равна алгебраической сумме проекций векторов на ту же ось, получим
 (7)
(7)
где 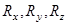 и
и 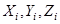 - проекции соответственно равнодействующей и сил системы на координатные оси.
- проекции соответственно равнодействующей и сил системы на координатные оси.
Модуль равнодействующей определяется по формуле
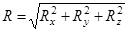 . (8)
. (8)
Для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая этих сил равнялась нулю.
Так как равнодействующая 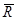 изображается вектором, замыкающим силовой многоугольник, то для того чтобы равнодействующая равнялась нулю, силовой многоугольник должен быть замкнутым, то есть конец вектора, изображающего последнюю силу, должен совпадать с началом вектора, изображающего первую силу.
изображается вектором, замыкающим силовой многоугольник, то для того чтобы равнодействующая равнялась нулю, силовой многоугольник должен быть замкнутым, то есть конец вектора, изображающего последнюю силу, должен совпадать с началом вектора, изображающего первую силу.
Таково условие равновесия системы сходящихся сил в геометрической форме. Выразим теперь то же условие аналитически.
Из (8) следует, что при равновесии должно иметь место равенство
 .
.
Так как все слагаемые в левой части не могут быть отрицательными, то это равенство справедливо только в случае, если 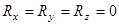 . С учетом (7), окончательно получим
. С учетом (7), окончательно получим
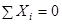 ,
, 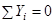 ,
, 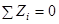 . (9)
. (9)
Следовательно, для равновесия системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех этих сил на каждую из трех координатных осей равнялась нулю.
Понятно, что в случае плоской системы сходящихся сил для равновесия должны быть выполнены только первые два из условий (9).
При решении задач статики иногда удобно пользоваться теоремой о трех силах: если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.
В большинстве случаев в задачах статики по заданным (известным) силам, приложенным к данному несвободному твердому телу, требуется определить неизвестные реакции связей, предполагая, что тело находится в покое и все приложенные к нему силы уравновешиваются. При аналитическом решении задачи эти силы находятся из уравнений (9), в левые части которых войдут, кроме заданных известных сил, и неизвестные реакции связей.
Рассмотрим примеры.
Пример 1. Шар веса 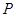 опирается в точке
опирается в точке 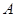 на наклонную плоскость, образующую с вертикалью угол
на наклонную плоскость, образующую с вертикалью угол 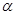 , и привязан к стене веревкой, которая образует с вертикалью угол
, и привязан к стене веревкой, которая образует с вертикалью угол 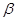 (рис.13а). Определить реакцию плоскости в точке
(рис.13а). Определить реакцию плоскости в точке 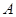 и натяжение веревки.
и натяжение веревки.
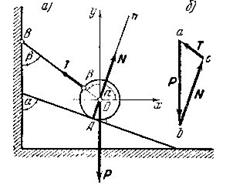
Рис.13
Решение: Обозначим искомую реакцию плоскости, направленную по нормали 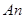 к этой плоскости, через
к этой плоскости, через 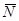 , а натяжение веревки – через
, а натяжение веревки – через 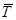 . Линия действия всех трех сил
. Линия действия всех трех сил 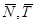 и
и 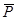 пересекаются в центре шара
пересекаются в центре шара  . Примем вертикаль и горизонталь в точке
. Примем вертикаль и горизонталь в точке 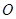 за координатные оси и найдем проекции сил
за координатные оси и найдем проекции сил 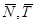 и
и 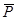 на эти оси:
на эти оси:
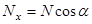 ,
, 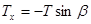 ,
,  ,
,
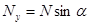 ,
, 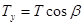 ,
, 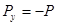 .
.
Так как данная система сходящихся сил является плоской, то условия равновесия (4) имеют вид
1) 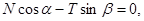
2) 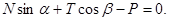
Умножив первое уравнение на 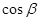 , а второе на
, а второе на 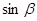 и сложив их, получим
и сложив их, получим
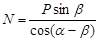 .
.
Затем из первого уравнения находим
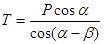 .
.
В случае, когда веревка, удерживающая шар, параллельна наклонной плоскости  , получим
, получим 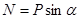 ,
, 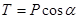 .
.
Для решения этой же задачи графическим способом, необходимо построить замкнутый силовой многоугольник. Построение силового многоугольника всегда нужно начинать с известных, заданных сил. Из произвольной точки  (рис.13б) проведем вектор
(рис.13б) проведем вектор 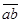 , параллельный данной силе
, параллельный данной силе 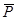 , длина которого в выбранном масштабе изображает модуль этой силы. Затем через точки
, длина которого в выбранном масштабе изображает модуль этой силы. Затем через точки 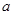 и
и 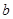 проводим прямые, параллельные линиям действия искомых сил
проводим прямые, параллельные линиям действия искомых сил 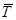 и
и  , которые пересекутся в точке
, которые пересекутся в точке 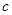 . Векторы
. Векторы 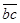 и
и  определяют искомые силы
определяют искомые силы  и
и 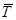 .Чтобы найти направление искомых сил на силовом треугольнике , нужно обойти этот треугольник по его периметру, причем направление этого обхода определяется направлением данной силы
.Чтобы найти направление искомых сил на силовом треугольнике , нужно обойти этот треугольник по его периметру, причем направление этого обхода определяется направлением данной силы 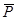 . Измерив длину сторон
. Измерив длину сторон 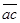 и
и 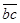 и зная масштаб, в котором построена сила
и зная масштаб, в котором построена сила 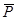 , найдем численные значения сил
, найдем численные значения сил 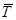 и
и  .
.
Пример 2. Определить реакции стержней, удерживающих грузы F1=70 кН и F2=100 кН (рис 14,а). Массой стержней пренебречь.
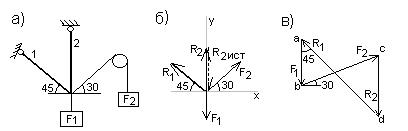
Рис.14
Указание. В данной задаче рассматривается равновесие плоской системы сходящихся сил и требуется определить реакции двух шарнирно соединенных между собой стержней, удерживающих два груза. Таким образом, к шарниру В в каждой задаче приложены четыре силы, из которых две неизвестны. Для задач такого типа универсальным является аналитический метод решения.
Последовательность решения задачи:
1. выбрать тело (точку), равновесие которого следует рассматривать;
2. освободить тело (шарнир В) от связей и изобразить действующие на него активные силы и реакции отброшенных связей. Причем реакции стержней следует направить от шарнира В, так как принять считать предположительно стержни растянутыми;
3. выбрать систему координат, совместив ее начало с точкой В, и составить уравнения равновесия, используя условия равновесия системы сходящихся сил на плоскости  ;
;
4. определить реакции стержней из решения указанной системы уравнений;
5. проверить правильность полученных результатов по уравнению, которое не использовалось при решении задачи, либо решить задачу графически.
Решение.
1. Рассматриваем равновесие шарнира В (рис 14,а)
2. Освобождаем шарнир В от связей и изображаем действующие на него активные силы и реакции связей (рис.14,б)
3. Выбираем систему координат и составляем уравнения равновесия для системы сил, действующих на шарнир В.

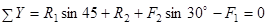
4. Определяем реакции стержней R1 и R2, решая уравнения.
Из уравнения 1: 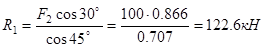
Подставляем найденное значение R1 в уравнение 2 и получаем
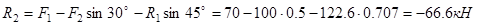
Знак минус перед значением R2 указывает на то, что первоначально выбранное направление реакции неверно – следует направить реакцию R2 в противоположную сторону, т.е. к шарниру В (на рис.14,б истинное направление реакции R2 показано штриховым вектором)
5. Проверяем правильность полученных результатов, решая задачу графически (рис. 14,в). Полученная система сил (рис.14,б) находится в равновесии, следовательно, силовой многоугольник, построенный для этой системы сил, должен быть замкнутым.
Строим силовой многоугольник в следующем порядке (рис.14,в): в выбранном масштабе (например, 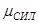 =2 кН/мм) откладываем заданную силу F1 (ab=F1), затем из точки b под углом 300 к горизонту откладываем силу F2 (bc=F2), далее из точек а и с проводим прямые, параллельные положениям стержней 1 и 2. Эти прямые пересекаются в точке d и в результате построения образуется замкнутый многоугольник a bcd, в котором сторона cd=R2, а сторона da=R1. Измерив длины этих сторон (в мм) и умножив на масштаб построения
=2 кН/мм) откладываем заданную силу F1 (ab=F1), затем из точки b под углом 300 к горизонту откладываем силу F2 (bc=F2), далее из точек а и с проводим прямые, параллельные положениям стержней 1 и 2. Эти прямые пересекаются в точке d и в результате построения образуется замкнутый многоугольник a bcd, в котором сторона cd=R2, а сторона da=R1. Измерив длины этих сторон (в мм) и умножив на масштаб построения 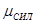 , получаем значения реакций стержней:
, получаем значения реакций стержней: 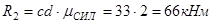
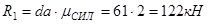
Графическое решение подтверждает правильность первого решения.
Плоская система сил
Пример 1. Определить реакции опор балки (рис.15, а).
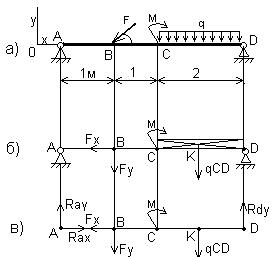
Рис.15
Указание. Во всех данных задачах требуется определить реакции опор балок. Учащимся необходимо приобрести навыки определения реакций опор, так как с этого начинается решение многих задач по сопротивлению материалов и деталям машин.
Последовательность решения задачи:
1. изобразить балку вместе с нагрузками;
2. выбрать расположение координатных осей, совместив ось х с балкой, а ось y направив перпендикулярно оси х;
3. произвести необходимые преобразования заданных активных сил: силу, наклоненную к оси балки под углом 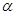 , заменить двумя взаимно перпендикулярными составляющими, а равномерно распределенную по закону прямоугольника нагрузку – ее равнодействующей, приложенной к середине участка распределения нагрузки;
, заменить двумя взаимно перпендикулярными составляющими, а равномерно распределенную по закону прямоугольника нагрузку – ее равнодействующей, приложенной к середине участка распределения нагрузки;
4. освободить балку от опор, заменив их действие реакциями опор, направленными вдоль выбранных осей координат;
5. составить уравнения равновесия статики для произвольной плоской системы сил таким образом и в такой последовательности, чтобы решением каждого из этих уравнений было определение одной из неизвестных реакций опор;
6. проверить правильность найденных опорных реакций по уравнению, которое не было использовано для решения задачи.
Решение.
1.Изобразим балку с действующими на нее нагрузками (рис.15,а)
2. Изобразим оси координат x и y
3. Силу F заменяем ее составляющими 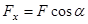 и
и  . Равнодействующая q С D равномерно распределенной нагрузки, приложенная в точке пересечения диагоналей прямоугольника (рис.15,б), переносится по линии своего действия в середину участка CD, в точку К.
. Равнодействующая q С D равномерно распределенной нагрузки, приложенная в точке пересечения диагоналей прямоугольника (рис.15,б), переносится по линии своего действия в середину участка CD, в точку К.
4. Освобождаем балку от опор, заменив их опорными реакциями (рис.15,в)
5. Составляем уравнения равновесия статики и определяем неизвестные реакции опор.
a) Из уравнения моментов всех действующих на балку сил, составленного относительно одной из точек опор, сразу определяем одну из неизвестных вертикальных реакций:

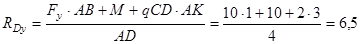 кН
кН
b) Определяем другую вертикальную реакцию:

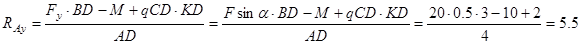 кН
кН
c) Определяем горизонтальную реакцию:
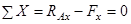 ;
; 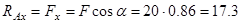 кН
кН
6. Проверяем правильность найденных результатов:
 .
.
Условие равновесия 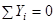 выполняется, следовательно, реакции опор найдены верно.
выполняется, следовательно, реакции опор найдены верно.
Пример 2. На вал (рис.16,а) жестко насажены шкив 1 и колесо 2. Определить силы F2, Fr2=0,4F2, а также реакции опор А и В если F1=100Н.
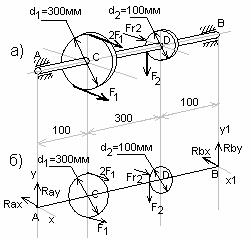
Рис.16
Указание.
Последовательность решения задачи:
1. изобразить на рисунке тело, равновесие которого рассматривается, с действующими на него активными и реактивными силами и выбрать систему координат;
2. из условия равновесия тала, имеющего неподвижную ось, определить значения сил F1, F2;
3. составить шесть уравнений равновесия;
4. решить уравнения и определить реакции опор;
5. проверить правильность решения задачи.
Решение.
1. Изображаем вал с всеми действующими на него силами, а также оси координат. (рис.16,б)
2. Определяем F2 и Fr2. Из условия равновесия тела, имеющего неподвижную ось:
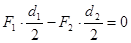 ;
;
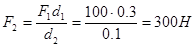 ;
;
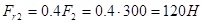
3. Составляем шесть уравнений равновесия:
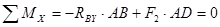 (1)
(1)
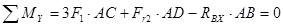 (2)
(2)
 (3)
(3)
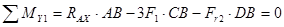 (4)
(4)
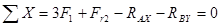 (5)
(5)
 (6)
(6)
4. Решаем уравнения (1), (2), (3), (4) и определяем реакции опор:
Из (1): 
Из (2): 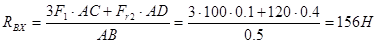
Из (3): 
Из (4): 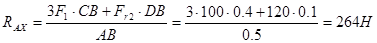
5. проверяем правильность найденных реакций опор. Используем уравнение (5)

 , следовательно, реакции RAX и RBX определены верно.
, следовательно, реакции RAX и RBX определены верно.
Используем уравнение (6):

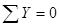 , следовательно, реакции RAY и RBY определены верно.
, следовательно, реакции RAY и RBY определены верно.
Данную задачу можно решать другим методом: спроектировать тело со всеми действующими на него активными и реактивными силами на три координатные плоскости, чтобы проще было составлять уравнения равновесия.
Система параллельных сил
Пусть на твердое тело действуют две параллельные силы 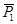 и
и  , направленные в одну сторону (рис.17).
, направленные в одну сторону (рис.17).
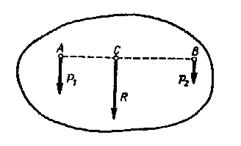
Рис.17
Равнодействующая 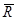 двух параллельных сил, направленных в одну сторону, параллельна этим силам и направлена в ту же сторону; модуль равнодействующей равен сумме модулей данных сил, а линия действия равнодействующей делит расстояние между точками приложения данных сил внутренним образом на части, обратно пропорциональные модулям этих сил, т.е.
двух параллельных сил, направленных в одну сторону, параллельна этим силам и направлена в ту же сторону; модуль равнодействующей равен сумме модулей данных сил, а линия действия равнодействующей делит расстояние между точками приложения данных сил внутренним образом на части, обратно пропорциональные модулям этих сил, т.е.
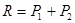 ;
; 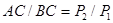 .
.
Используя известное свойство пропорции, можно получить
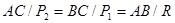 .
.
Пусть теперь имеем две параллельные силы 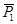 и
и  , приложенные в точках
, приложенные в точках 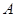 и
и  и направленные в противоположные стороны; такие силы называются антипараллельными (рис.18).
и направленные в противоположные стороны; такие силы называются антипараллельными (рис.18).

Рис.18
Предположим, что 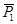 >
>  . Равнодействующая
. Равнодействующая 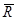 двух антипараллельных сил параллельна этим силам и направлена в сторону большей силы; модуль равнодействующей равен разности модулей данных сил, а линия ее действия делит расстояние между точками приложения данных сил внешним образом на части, обратно пропорциональные модулям этих сил, т.е.
двух антипараллельных сил параллельна этим силам и направлена в сторону большей силы; модуль равнодействующей равен разности модулей данных сил, а линия ее действия делит расстояние между точками приложения данных сил внешним образом на части, обратно пропорциональные модулям этих сил, т.е.
 ;
; 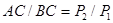 и
и  .
.
Как видно, в этом случае линия действия равнодействующей 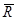 проходит через точку, лежащую вне отрезка
проходит через точку, лежащую вне отрезка 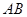 , и притом ближе к большей силе.
, и притом ближе к большей силе.
Рассмотрим систему параллельных сил 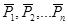 , приложенных в точках
, приложенных в точках 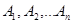 , приводящуюся к равнодействующей
, приводящуюся к равнодействующей 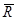 , приложенной в точке
, приложенной в точке  (рис.19).
(рис.19).
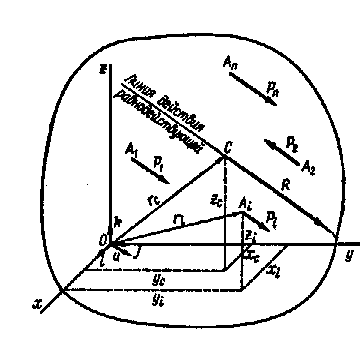
Рис.19
Положение центра параллельных сил  определится его радиусом-вектором
определится его радиусом-вектором 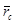 относительно начала координат
относительно начала координат 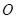 или тремя координатами
или тремя координатами 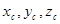 . Положение точки приложения каждой силы
. Положение точки приложения каждой силы 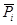 определяется радиусом-вектором
определяется радиусом-вектором 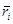 или координатами
или координатами 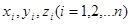 .
.
Опуская выкладки, приведем формулу, определяющую радиус-вектор центра параллельных сил
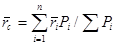 . (10)
. (10)
Спроектировав равенство (5) на оси координат, получим формулы для определения координат центра параллельных сил
 ;
; 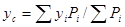 ;
;  . (11)
. (11)
В формулах (11) координаты 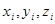 и значения сил
и значения сил 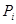 являются алгебраическими величинами. Заметим, что выбор направления, вдоль которого параллельные силы считаются положительными, произволен и на результатах вычисления координат по формулам (11) не отражается.
являются алгебраическими величинами. Заметим, что выбор направления, вдоль которого параллельные силы считаются положительными, произволен и на результатах вычисления координат по формулам (11) не отражается.
Пусть даны параллельные силы 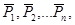 расположенные на плоскости
расположенные на плоскости 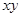 , и приложенные в точках
, и приложенные в точках  . Приведем силы к произвольному центру
. Приведем силы к произвольному центру 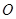 (рис.20). Получим в этом центре силу
(рис.20). Получим в этом центре силу  , равную главному вектору, и пару сил с моментом
, равную главному вектору, и пару сил с моментом 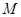 , равным главному моменту параллельных сил относительно центра приведения
, равным главному моменту параллельных сил относительно центра приведения
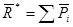 ;
;  . (12)
. (12)
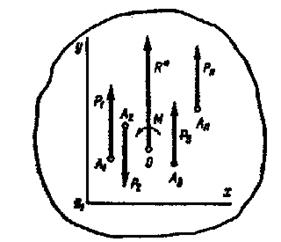
Рис.20
Для системы параллельных сил на плоскости имеем два условия равновесия
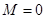 и
и  . (13)
. (13)
Так как ось 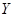 направлена параллельно силам, то из (12) и (13) уравнения равновесия для данной системы сил можно выразить в виде двух уравнений
направлена параллельно силам, то из (12) и (13) уравнения равновесия для данной системы сил можно выразить в виде двух уравнений
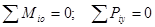 . (14)
. (14)
Уравнения (14) называются основными уравнениями равновесия параллельных сил на плоскости. Центр моментов для этой системы уравнений можно выбирать произвольно.
Для пространственной системы сил, параллельных, например, оси  , имеем три уравнения равновесия
, имеем три уравнения равновесия
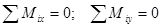 ;
;  .
.
Рассмотрим несколько примеров.
Пример 1.На тело действуют пять параллельных сил, имеющих модули  ,
,  и
и  , приложенных соответственно в точках
, приложенных соответственно в точках 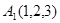 ,
, 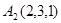 ,
, 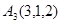 ,
, 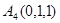 и
и 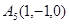 , причем первые четыре силы направлены в одну и ту же сторону, а последняя - в противоположную сторону. Найти координаты центра этой системы сил.
, причем первые четыре силы направлены в одну и ту же сторону, а последняя - в противоположную сторону. Найти координаты центра этой системы сил.
Решение. Полагая в формулах (14) для координат центра параллельных сил
 ,
, 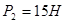 ,
, 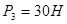 ,
, 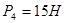 ,
,  и
и 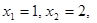
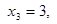
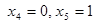 , получим
, получим
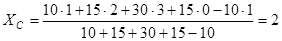 .
.
Аналогично, найдем две другие координаты точки 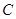
 .
.
Пример 2. К горизонтальной балке, лежащей на двух опорах, приложены вертикальные силы  и
и 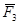 . Расстояния точек приложения этих сил от опор и расстояние между опорами указаны на рис.18. Определить реакции опор.
. Расстояния точек приложения этих сил от опор и расстояние между опорами указаны на рис.18. Определить реакции опор.
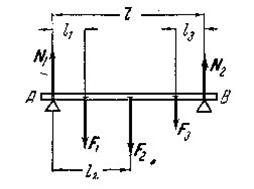
Рис.21
Решение. Обозначим реакции опор через 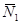 и
и  . Поскольку балка находится в равновесии, направив ось
. Поскольку балка находится в равновесии, направив ось 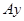 вертикально вверх, составим уравнения равновесия (9) для данной задачи
вертикально вверх, составим уравнения равновесия (9) для данной задачи
1) 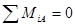
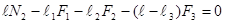
2) 
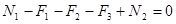
Из первого уравнения получим
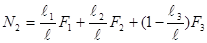 .
.
Подставив значение 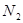 во второе уравнение, найдем
во второе уравнение, найдем 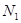
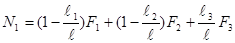 .
.
Дата добавления: 2020-11-27; просмотров: 582; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!