Классическое определение вероятности
Математика (05.11.2020)
Работу на проверку предоставить до 09.11.2020 (не позднее 10.00). Работа, отправленная позже указанной даты, проверяться не будет.
1. Теоретическая часть. Изучить тему «События и вероятности».
2. Подготовить сообщение на тему «История развития комбинаторики, теории вероятностей и статистики и их роль в различных сферах человеческой жизнедеятельности».
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
События и вероятности
Каждая наука, развивающая общую теорию какого-либо явления, содержит ряд основных понятий, на которых она базируется. Такие основные понятия существуют и в теории вероятностей. Современное изложение их основано на теории множеств. Однако вначале здесь мы будем придерживаться подхода, основанного на реальном содержании вводимых понятий и соотношений, что, несомненно, облегчит понимание основ теории вероятностей.
Одним из основных понятий теории вероятностей является случайное событие, или просто событие.
Классификация событий
Опытом, или испытанием, называется всякое осуществление определенного комплекса условий или действий, при которых происходит соответствующее явление. Возможный результат опыта называется событием. Например, опытом является подбрасывание монеты, а событием «герб», «цифра на верхней ее стороне» (когда монета упадет). Опытом является стрельба по мишени, извлечение шара из ящика и т.п. События будем обозначать заглавными буквами латинского алфавита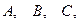 
…
|
|
|
Событие называется достоверным в данном опыте, если оно обязательно произойдет в этом опыте. Например, если в ящике находятся только голубые шары, то событие «из ящика извлечен голубой шар» является достоверным (в ящике нет шаров другого цвета).
Событие называется невозможным в данном опыте, если оно не может произойти в этом опыте. Так, если в ящике находятся только красные шары, то событие «из ящика извлечен голубой шар» является невозможным (таких шаров в ящике нет).
Событие называется случайным в данном опыте, если оно может произойти, а может не произойти в этом опыте. Например, если в ящике находятся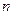 
голубых и 
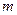красных шаров, одинаковых по размеру и весу, то событие «из ящика извлечен голубой шар» является случайным (оно может произойти, а может не произойти, поскольку в ящике имеются не только голубые, но и красные шары). Случайными событиями являются «герб» и « цифра на верхней ее стороне монеты при ее подбрасывании», «попадание и промах при стрельбе по мишени», «выигрыш по билету лотереи» и т.п.
Замечание. Приведенные примеры свидетельствуют о том, что одно и то же событие в некотором опыте может быть достоверным, в другом – невозможным, в третьем – случайным. Говоря о достоверности, невозможности, случайности события, имеют в виду его достоверность, невозможность, случайность по отношению к конкретному опыту, т.е. к наличию определенного комплекса условий или действий. Событие, которое происходит при осуществлении определенного комплекса условий, называется достоверным. Событие, которое никогда не происходит при выполнении комплекса условий, называется невозможным. Событие называется случайным при выполнении комплекса условий, если при выполнении этого комплекса оно то происходит, то не происходит.
|
|
|
Два событие называются совместными в данном опыте, если появление одного из них не исключает появление другого в этом опыте. Так, при подбрасывании двух симметричных монет, событие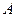 
– «герб на верхней стороне первой монеты» и 
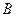– «цифра на верхней стороне второй монеты» являются совместными.
Два события называются несовместными, если они не могут произойти вместе при одном и том же испытании. Например, несовместными являются попадание и промах при одном выстреле.
Несколько событий называются несовместными, если они попарно несовместны.
|
|
|
Два события называются противоположными, если появление одного из них равносильно непоявлению другого. Так, противоположными являются события «герб» и «цифра» при одном подбрасывании симметричной монеты. Если одно из противоположных событий обозначено буквой 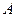, то другое обозначают 
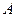. Например, если - «попадание», то - «промах» при одном выстреле по мишени.
Множество событий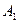 
, 
, … , 
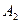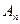. Называют полной группой событий, если они попарно-несовместны; появление одного и только одного из них является достоверным событием. Поясним понятие полной группы событий на следующем примере. Рассмотрим события, появляющиеся при подбрасывании игрального кубика (т.е. кубика, на гранях которого записаны цифры 1, 2, 3, 4, 5, 6 или изображены знаки, соответствующие этим цифрам.) Когда кубик упадет, то верхней гранью окажется грань с одной из этих цифр. Событие: «верхней гранью оказалась грань с цифрой 
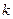» обозначим через 
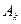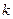( = 1, 2, 3, 4, 5, 6). События , , 
, 
, 
, 
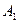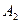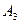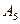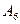образуют полную группу: они попарно-несовместны; появление одного и только одного из низ является достоверным событием (когда кубик упадет, то только одна из граней окажется верхней, на ней написана только одна из цифр от 1 до 6).
|
|
|
События считают равновозможными, если нет оснований полагать, что одно событие является более возможным, чем другие. Например, при подбрасывании монеты событие 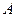(появление цифры) и событие 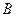(появление герба) равновозможны, так как предполагается, что монета изготовлена из однородного материала, имеет правильную цилиндрическую форму и наличие чеканки не влияет на то, какая сторона монеты (цифра или герб) окажется верхней. При подбрасывании игрального кубика события 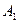, , 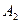, , 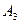, 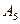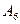являются равновозможными, поскольку предполагается, что кубик изготовлен из однородного материала, имеет правильную форму и наличие цифр (или очков) на гранях не влияет на то, какая из шести граней окажется верхней.
Каждое событие, которое может наступить в итоге опыта, называется элементарным исходом (элементарным событием, или шансом). Например, события 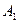, , 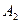, , 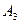, 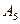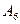- элементарные исходы при подбрасывании кубика.
Элементарные исходы, при которых данное событие наступает, называются благоприятствующими этому событию, или благоприятными шансами. Так, при подбрасывании игрального кубика элементарные исходы 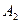, , 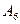являются благоприятствующими события «выпало четное число очков».
Пример 1. Подбрасываются два игральных кубика, подсчитываются суммы выпавших очков (суммы числа очков на верхних гранях обоих кубиков). Сумма выпавших очков на двух кубиках может меняться от 2 до 12. Записать полную группу событий в этом опыте.
Решение. Полную группу событий образуют равновозможные элементарные исходы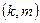 
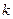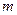, , =1,2,3,4,5,6, представленные в таблице 1.1. Элементарный исход 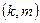означает, что на первом кубике выпало 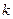очков, на втором 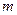очков ( 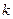, 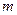=1,2,3,4,5,6).
| (1;1) | (2;1) | (3;1) | (4;1) | (5;1) | (6;1) |
| (1;2) | (2;2) | (3;2) | (4;2) | (5;2) | (6;2) |
| (1;3) | (2;3) | (3;3) | (4;3) | (5;3) | (6;3) |
| (1;4) | (2;4) | (3;4) | (4;4) | (5;4) | (6;4) |
| (1;5) | (2;5) | (3;5) | (4;5) | (5;5) | (6;5) |
| (1;6) | (2;6) | (3;6) | (4;6) | (5;6) | (6;6) |
Пример 2. Сколько элементарных исходов благоприятствует событию «на обоих кубиках выпало одинаковое число очков» при подбрасывании двух игральных кубиков?
Решение. Этому событию благоприятствуют 6 элементарных исходов: (1;1), (2;2), (3;3), (4;4), (5;5), (6;6).
Пример 3. Подбрасывается два игральных кубика. Какому событию благоприятствует больше элементарных исходов: «сумма выпавших очков равна 7», «сумма выпавших очков равна 8»?
Решение. Событию «сумма выпавших очков равна 7» благоприятствуют 6 исходов: (1;6), (2;5).(3;4), (4;3), (5;2), (6;1). Событию «сумма выпавших очков равна 8» благоприятствуют 5 исходов: (2;6), (3;5), (4;4), (5;3), (6;2). Следовательно, первому событию благоприятствует больше элементарных исходов.
Пример 4. Подбрасываются три игральных кубика, подсчитываются суммы очков, выпавших на них. Сколькими способами можно получить в сумме 5 очков, 6 очков?
Решение. Получить в сумме 5 очков можно 6 способами: (1;1;3), (1;3;1), (3;1;1), (1;2;2), (2;1;2), (2;2;1).Получить в сумме 6 очков можно 10 способами: (1;1;4), (1;4;1), (4;1;1), (1;2;3), (1;3;2), (2;1;3), (2;3;1), (3;1;2), (3;2;1), (2;2;2).
Классическое определение вероятности
Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных исходов опыта, в котором может появиться это событие. Вероятность события 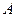обозначается через 
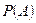(здесь 
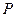- первая буква французского слова probabilite - вероятность). В соответствии с определением
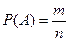(1.2.1)
где 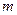- число элементарных исходов, благоприятствующих событию 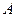; 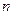- число всех равновозможных элементарных исходов опыта, образующих полную группу событий.
Это определение называется классическим. Оно возникло на начальном этапе развития теории вероятностей.
Вероятность события имеет следующие свойства:
1. Вероятность достоверного события равна единице. Обозначим достоверное событие буквой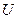 
. Для достоверного события 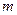= 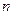, поэтому
. (1.2.2)
2. Вероятность невозможного события равна нулю. Обозначим невозможное событие буквой 
. Для невозможного события 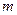=0, поэтому
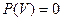. (1.2.3)
3. Вероятность случайного события выражается положительным числом, меньшим единицы. Поскольку для случайного события 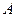выполняется неравенства 
, или 
, то
. (1.2.4)
4. Вероятность любого события 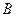удовлетворяет неравенствам
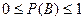. (1.2.5)
Это следует из соотношений (1.2.2) - (1.2.4).
Пример 1. В урне 10 одинаковых по размеру и весу шаров, из которых 4 красных и 6 синих. Из урны извлекается один шар. Какова вероятность того, что извлеченный шар окажется синим?
Решение. Событие «извлеченный шар оказался синим» обозначим буквой 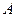. Данное испытание имеет 10 равновозможных элементарных исходов, из которых 6 благоприятствуют событию 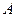. В соответствии с формулой (1.2.1) получаем
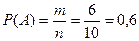
Пример 2. Все натуральные числа от 1 до 30 записаны на одинаковых карточках и помещены в урну. После тщательного перемешивания карточек из урны извлечена одна карточка. Какова вероятность того, что число на взятой карточке окажется кратным 5?
Решение. Обозначим через 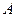событие «число на взятой карточке кратно 5». В данном испытании имеется 30 равновозможных элементарных исходов, из которых событию 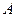благоприятствуют 6 исходов (числа 5, 10, 15, 20, 25, 30). Следовательно,
Пример 3. Подбрасывают два игральных кубика, подсчитывается сумма очков на верхних гранях. Найти вероятность события 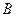, состоящего в том, что на верхних гранях кубиков в сумме будет 9 очков.
Решение. В этом испытании всего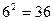 
равновозможных элементарных исходов. Событию 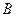благоприятствуют 4 исхода (3;6), (4;5), (5;4), (6;3), поэтому
.
Пример 4. Из слова дифференциал наугад выбрана одна буква. Какова вероятность того, что эта буква будет: а) гласной, б) согласной, в) буквой ч?
Решение. В слове дифференциал 12 букв, из них 5 гласных и 7 согласных. Буквы ч в этом слове нет. Обозначим события: 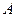- «гласная буква», 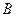- «согласная буква», 
- «буква ч». Число благоприятствующих элементарных исходов: 
=5 – для события ,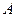 
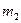=7 – для события , 
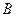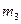=0 – для события . Поскольку 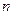=12, то
; 
; 
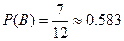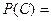0.
Комбинаторика и вероятность
Комбинаторика изучает способы подсчета числа элементов в конечных множествах. Формулы комбинаторики используются при непосредственном вычислении вероятностей.
Множества элементов, состоящие из одних и тех различных элементов и отличающиеся друг от друга только их порядком, называются перестановками этих элементов. Число всевозможных перестановок из 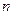элементов обозначается через 
; это число равно 
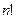(читается « n факториал»):
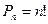(1.3.1)
где
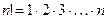. (1.3.2)
Например, 3!=1*2*3=6
4!=1*2*3*4=24
5!=1*2*3*4*5=120
Замечание 1: Для пустого множества принимается соглашение: пустое множество можно упорядочить только одним способом; по определению полагают 0!=1.
Размещениями называют множества, составленные из 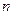различных элементов по 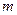элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений определяется формулой
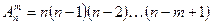(1.3.3)
Сочетаниями из 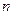различных элементов по 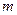называются множества, содержащие 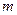элементов из числа 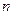заданных, и которые отличаются хотя бы одним элементом. Число сочетаний из 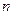элементов по 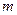обозначают: 
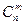или 
. Это число выражается формулой
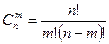(1.3.4)
Пример 1. На пяти одинаковых карточках написаны буквы И, К, М, Н, С. Карточки перемешиваются и наугад раскладываются в ряд. Какова вероятность того, что получится слово МИНСК?
Решение. Из пяти различных элементов можно составит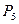 
перестановок: 
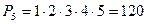. Значит, всего равновозможных исходов будет 120, а благоприятствующий данному событию – только один. Следовательно,
.
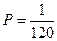Пример 2. Из букв слова ротор, составленного с помощью разрезной азбуки, наудачу последовательно извлекаются 3 буквы и складываются в ряд. Какова вероятность того, что получится слово тор?
Решение. Чтобы отличить одинаковые буквы друг от друга, снабдим их номерами: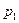 
, 
, 
, 
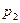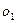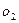. Общее число элементарных исходов равно: 
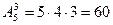. Слово ротор получится в 
случаях (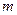 
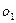
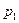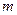
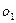
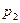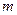
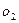
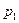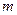
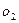
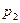, , , ). Искомая вероятность равна
.
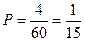При подсчете благоприятных случаев здесь воспользовались правилом произведения: буквы т можно выбрать одним способом, буквы о – двумя, букву р – двумя способами.
Дата добавления: 2020-11-27; просмотров: 253; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!