Основные свойства неопределенного интеграла.
Лекция (к занятию № 30)
Тема. Неопределенный интеграл и его свойства. Табличные интегралы. Геометрический смысл неопределенного интеграла.
План.
1. Понятие первообразной функции.
2. Неопределенный интеграл.
3. Основные свойства неопределенного интеграла.
4. Таблица простых интегралов.
5. Интегралы, не выражающиеся в элементарных функциях.
6. Непосредственное интегрирование.
Понятие первообразной функции.
Одной из главных задач дифференциального исчисления является задача нахождения производной (или дифференциала). На практике часто приходится решать обратную задачу: зная производную функции, найти эту функцию. Эта операция называется интегрированием.
По данному выражения  или,
или, 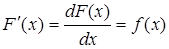
де¦(х) - известная функция, нужно найти функцию F (х). Искомая функция F (x) называется первообразной функцией по отношению к функции ¦(х). Дадим определение первообразной функции.
Определение 1. Первообразной функцией для данной функции ¦(х)на промежутке Х называется такая функция F (x), производная которой равняется ¦(х) (или, что, то же самое, дифференциал которой равен ¦(х)dx). Например, первообразной функцией для функции 5х4 является х5, поскольку (х5) ¦(х) = 5х4. Эта первообразная не единственная, а только одна из многих, так как функции х5 + C, где C - постоянная, тоже есть первообразной для ¦(х) = 5х4, потому что (х5 + C).= 5х4.
Теорема 1. Если на некотором промежутке функция F (x) является первообразной для функции¦(х), то для ¦(х) будет первообразной и любая функция вида
|
|
|
Ф (х) = F (x) + С (1)
где С - произвольная постоянная.
Доказательство. Пусть Ф(х) и F(х) - две функции, которые являются первообразными для функции ¦(х) на некотором промежутке. Тогда на этом промежутке, 
Откуда Ф (х) - F (x) = С и, тем самым, Ф (х) = F(x) - С.
Геометрически, соотношение (1) означает, что графики всех первообразных для данной функции ¦(х) представляют собой семейство таких кривых, которые могут быть получены с каждой из них путем ее сдвиг вдоль оси координат.
Неопределенный интеграл.
Определение 2. Совокупность всех первообразных функций для функции ¦(х) на промежутке Х называется неопределенным интегралом от функции ¦(х) на этом промежутке и обозначается символом
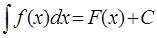 (2)
(2)
Функция ¦(х) называется подинтегральной функцией, а выражение ¦(х)dx называется подынтегральным выражением, знак ∫ называется знаком интеграла, переменная х - переменной интегрирования.
Операция нахождения первоначальной по ее производной или неопределенном интеграле по заданной подынтегральной функции называется интегрированием этой функции. Интегрирование является операцией, обратной дифференцированию. Для проверки правильности исчисления интеграл нужно продифференцировать и получить при этом подынтегральную функцию.
|
|
|
Пример 1. Найти интеграл ∫2х dx.
Решение. Одной из первоначальных есть функция х2. Откуда следует, что
∫2х dx = х2 + С
Пример 2. Вычислить. 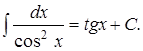
Решение. Находим функцию, производная которой равна 1/соs2х:
(tgх)¢= = 1/соs2х. Итак, 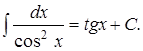
Основные свойства неопределенного интеграла.
1. Производная неопределенного интеграла равна подынтегральной функции, а дифференциал неопределенного интеграла равен подынтегральному выражению.
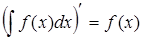 , (3)
, (3)
 , (4)
, (4)
Доказательство. Продифференцируем левую и правую части равенства (2): 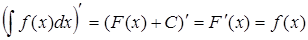
Аналогично, для дифференциала: 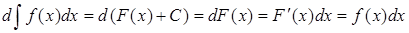
2. Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная:
∫dF (x) = F (x) + С (5)
Доказательство. По определению, ∫d¦(х)= F (x) + С, но d = F ((x) dх, тогда
∫dF = F (x) + С
3. Постоянный множитель можно выносить за знак неопределенного интеграла:
∫а¦(х)dх = а∫¦(х)dх (а ≠ 0). (6)
Доказательство. Пусть ∫¦(х)dх = F(x) + С. Тогда правую часть (6) можно записать так: а(F(x) + С) = а(x) + ас.. (6a)
При a ≠ 0, ас = const. Производная (6а) равна
(аF(х)+аС)¢ = а F¢(х) = а¦(х).
Согласно определению неопределенного интеграла, свойство доказано.
|
|
|
4. Неопределенный интеграл от суммы двух непрерывных функций равен сумме неопределенных интегралов от этих функций:
.  (7)
(7)
Доказательство. Пусть F1(х) - первообразная для ¦1(х), а F2(х) – первообразная для ¦2(х). Тогда правую часть равенства (7) можно записать в виде F1(х) ± F2(х) +С1 ± С2, где С1 и С2 - произвольные постоянные. Поскольку С1 ± С2 тоже будет произвольной постоянной, а производная от F1(х) ± F2(х) равна подинтегральной функции по левой части равенства
[F1(х) ± F2(х) ]¢= F1 ¢(х) ± F2 ¢(х) = ¦1(х) ± ¦2(х),
то согласно определению, свойство доказана.
Свойство 4, остается справедливого для любого конечного числа слагаемых.
Таблица простейших интегралов.
Поскольку интегрирование есть действие обратное дифференцированию, получим таблицу простейших интегралов, используя формулы дифференцирования.
1. 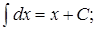
2. 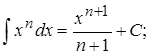
3. 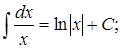
4. 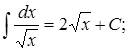
5. 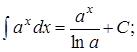
6. 
7. 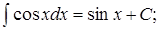
8. 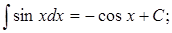
9. 
10. 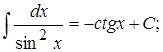
11. 
12. 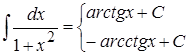
13. 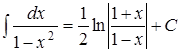
14. 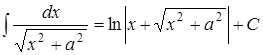
Эти интегралы называют табличными и их необходимо запомнить.
Дата добавления: 2020-11-27; просмотров: 81; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
