Оценка истинного значения измеряемой величины.
Лекция 6. Статистические оценки параметров распределения. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
Точечные статистические оценки 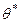 являются случайными величинами, поэтому приближенная замена неизвестного параметра распределения
являются случайными величинами, поэтому приближенная замена неизвестного параметра распределения 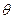 на
на 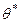 часто приводит к существенным ошибкам, особенно при малом объеме выборки. В этом случае применяют интервальные статистические оценки.
часто приводит к существенным ошибкам, особенно при малом объеме выборки. В этом случае применяют интервальные статистические оценки.
Интервальной называется оценка, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр. Интервальные оценки позволяют установить точность и надежность оценок.
Разность между статистической оценкой 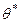 и оцениваемым ею параметром
и оцениваемым ею параметром 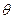 , взятая по абсолютной величине, называется точностью оценки, а именно
, взятая по абсолютной величине, называется точностью оценки, а именно
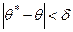 , (1)
, (1)
где 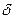 – точность оценки.
– точность оценки.
Так как 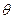 – случайная величина, то и
– случайная величина, то и 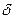 будет случайной величиной, поэтому неравенство (1) выполняется с определенной вероятностью.
будет случайной величиной, поэтому неравенство (1) выполняется с определенной вероятностью.
Вероятность, с которой берется неравенство (1), то есть
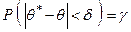 , (2)
, (2)
называется надежностью (доверительной вероятностью). Обычно надежность оценки задается наперед, причем в качестве 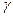 берут число, близкое к единице. Наиболее часто задают надежность, равную
берут число, близкое к единице. Наиболее часто задают надежность, равную 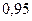 ;
; 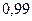 и
и 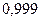 .
.
Равенство (2) можно записать так
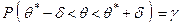 , (3)
, (3)
Интервал 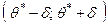 , покрывающий оцениваемый параметр
, покрывающий оцениваемый параметр 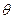 генеральной совокупности с заданной надежностью
генеральной совокупности с заданной надежностью 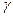 , называют доверительным.
, называют доверительным.
|
|
|
Доверительные интервалы для оценки математического ожидания 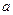 нормального распределения при известном среднем квадратическом отклонении
нормального распределения при известном среднем квадратическом отклонении 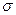 .
.
Пусть количественный признак 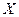 генеральной совокупности распределен нормально, причем среднее квадратическое отклонение этого распределения известно. Требуется оценить неизвестное математическое ожидание
генеральной совокупности распределен нормально, причем среднее квадратическое отклонение этого распределения известно. Требуется оценить неизвестное математическое ожидание 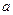 по выборочной средней
по выборочной средней 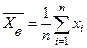 . Найдем доверительные интервалы, покрывающие параметр
. Найдем доверительные интервалы, покрывающие параметр 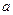 с надежностью
с надежностью 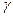 .
.
Будем рассматривать выборочную среднюю 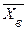 как случайную величину
как случайную величину 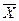 (
( 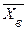 изменяется от выборки к выборке) и выборочные значения признака
изменяется от выборки к выборке) и выборочные значения признака 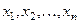 , как одинаково распределенные независимые случайные величины
, как одинаково распределенные независимые случайные величины  (эти числа также изменяются от выборки к выборке). Математическое ожидание каждой из этих величин равно
(эти числа также изменяются от выборки к выборке). Математическое ожидание каждой из этих величин равно 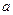 и среднее квадратическое отклонение –
и среднее квадратическое отклонение – 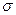 .
.
Если случайная величина 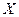 распределена нормально, то выборочная средняя
распределена нормально, то выборочная средняя 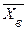 , найденная по независимым наблюдениям, также распределена нормально. Параметры распределения
, найденная по независимым наблюдениям, также распределена нормально. Параметры распределения 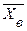 таковы
таковы
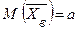 ,
, 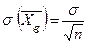 .
.
Потребуем, чтобы выполнялось соотношение
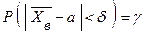 ,
,
где 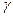 – заданная надежность.
– заданная надежность.
Пользуясь формулой
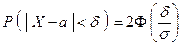 ,
,
|
|
|
заменив 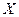 на
на 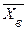 и
и 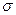 на
на 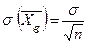 , получим
, получим
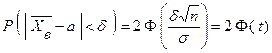 ,
,
где 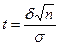 .
.
Найдя из последнего равенства 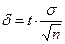 , можем написать
, можем написать
 ,
,
Окончательно имеем
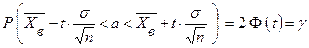 . (4)
. (4)
Смысл полученного соотношения таков: с надежностью 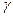 можно утверждать, что доверительный интервал
можно утверждать, что доверительный интервал  покрывает неизвестный параметр
покрывает неизвестный параметр 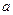 ; точность оценки
; точность оценки 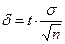 . Число
. Число 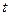 можно определить из равенства
можно определить из равенства 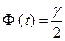 по таблице функции Лапласа.
по таблице функции Лапласа.
Итак, поставленная задача решена.
Замечание 1. Оценку 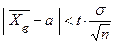 называют классической. Из формулы
называют классической. Из формулы 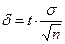 , определяющей точность классической оценки, можно сделать следующие выводы:
, определяющей точность классической оценки, можно сделать следующие выводы:
1) при возрастании объема выборки 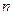 число
число 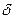 убывает и, следовательно, точность оценки увеличивается;
убывает и, следовательно, точность оценки увеличивается;
2) увеличение надежности оценки 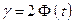 приводит к увеличению
приводит к увеличению 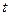 (
( 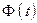 – возрастающая функция), а следовательно, и к возрастанию
– возрастающая функция), а следовательно, и к возрастанию 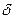 ; иными словами, увеличение надежности классической оценки влечет за собой уменьшение ее точности.
; иными словами, увеличение надежности классической оценки влечет за собой уменьшение ее точности.
Замечание 2. Если требуется оценить математическое ожидание с наперед заданной точностью 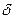 и надежностью
и надежностью 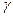 , то минимальный объем выборки, который обеспечит эту точность, находят по формуле
, то минимальный объем выборки, который обеспечит эту точность, находят по формуле
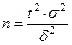 ,
,
которая является следствием равенства 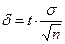 .
.
Доверительные интервалы для оценки математического ожидания 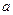 нормального распределения при неизвестном среднем квадратическом отклонении
нормального распределения при неизвестном среднем квадратическом отклонении 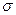 .
.
|
|
|
Пусть количественный признак 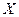 генеральной совокупности распределен нормально, причем среднее квадратическое отклонение
генеральной совокупности распределен нормально, причем среднее квадратическое отклонение 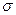 этого распределения неизвестно. Требуется оценить неизвестное математическое ожидание
этого распределения неизвестно. Требуется оценить неизвестное математическое ожидание 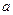 при помощи доверительных интервалов.
при помощи доверительных интервалов.
По данным выборки построим случайную величину
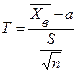 ,
,
которая имеет распределение Стьюдента с  степенями свободы; здесь
степенями свободы; здесь 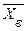 – выборочная средняя,
– выборочная средняя, 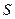 – исправленное среднее квадратическое отклонение,
– исправленное среднее квадратическое отклонение, 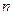 – объем выборки.
– объем выборки.
Дифференциальная функция
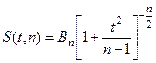 ,
,
где  .
.
Видно, что распределение Стьюдента определяется параметром 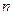 – объемом выборки (или, что то же, числом степеней свободы
– объемом выборки (или, что то же, числом степеней свободы  ) и не зависит от неизвестных параметров
) и не зависит от неизвестных параметров 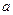 и
и 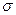 , что является его большим достоинством. Поскольку
, что является его большим достоинством. Поскольку 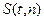 – четная функция от
– четная функция от 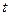 , вероятность выполнения неравенства
, вероятность выполнения неравенства  определяется так
определяется так
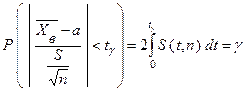 .
.
Заменив неравенство в круглых скобках равносильным ему двойным неравенством, получим
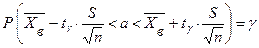 . (5)
. (5)
По заданным 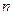 и
и 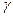 можно найти табличное значение
можно найти табличное значение 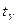 . Итак, доверительный интервал найден.
. Итак, доверительный интервал найден.
Замечание. Из предельных соотношений
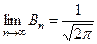 ,
, 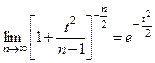
следует, что при неограниченном возрастании объема выборки 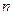 распределение Стьюдента стремится к нормальному. Поэтому при
распределение Стьюдента стремится к нормальному. Поэтому при 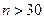 можно вместо распределения Стьюдента пользоваться нормальным распределением. Однако важно подчеркнуть, что для малых выборок (
можно вместо распределения Стьюдента пользоваться нормальным распределением. Однако важно подчеркнуть, что для малых выборок ( 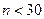 ), замена распределения нормальным приводит к грубым ошибкам, а именно – к неоправданному сужению доверительного интервала, то есть к повышению точности оценки.
), замена распределения нормальным приводит к грубым ошибкам, а именно – к неоправданному сужению доверительного интервала, то есть к повышению точности оценки.
|
|
|
То обстоятельство, что распределение Стьюдента при малой выборке дает широкий доверительный интервал, вовсе не свидетельствует о слабости метода Стьюдента, а объясняется тем, что малая выборка, разумеется, содержит малую информацию об интересующем нас признаке.
Построение доверительного интервала для оценки математического ожидания с помощью неравенства Чебышева при заданной надежности 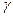 .
.
В том случае, когда отсутствует информация о законе распределения признака генеральной совокупности 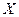 , оценивание вероятности события
, оценивание вероятности события 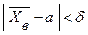 , где
, где 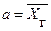 , и построение доверительного интервала для
, и построение доверительного интервала для 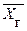 с заданной надежностью
с заданной надежностью 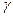 производится с использованием неравенства Чебышева при условии, что известно значение
производится с использованием неравенства Чебышева при условии, что известно значение 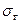 , а именно
, а именно
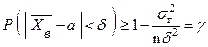 . (6)
. (6)
Из (6) определяем величину 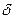
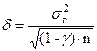 . (7)
. (7)
Доверительный интервал задается таким неравенством
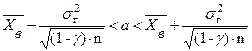 . (8)
. (8)
Когда 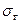 неизвестно, используем исправленное среднее квадратическое отклонение
неизвестно, используем исправленное среднее квадратическое отклонение 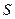 , а доверительный интервал имеет вид
, а доверительный интервал имеет вид
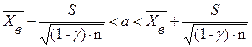 . (9)
. (9)
Пример. Получены данные со 100 наугад выбранных предприятий о возрастании выработки на одного работника 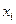 (в % относительно предыдущего года), которые имеют такое интервальное статистическое распределение
(в % относительно предыдущего года), которые имеют такое интервальное статистическое распределение
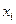 , %; , %; 
| 80 – 90 | 90 – 100 | 100 – 110 | 110 – 120 | 120 – 130 |
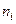
| 3 | 14 | 60 | 20 | 4 |
Используя неравенство Чебышева, построить доверительный интервал для 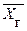 , если известно значение
, если известно значение 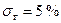 с надежностью
с надежностью 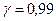 .
.
Решение. Для построения доверительного интервала с помощью неравенства Чебышева необходимо вычислить 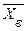 и
и 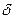 . Чтобы определить
. Чтобы определить 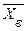 , перейдем от интервального к дискретному статистическому распределению, а именно
, перейдем от интервального к дискретному статистическому распределению, а именно
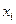
| 85 | 95 | 105 | 115 | 125 |
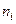
| 3 | 14 | 60 | 20 | 4 |
Тогда имеем
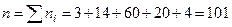 .
.
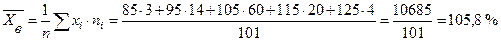 .
.
Используя (13.7), вычислим 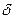
 .
.
По формуле (13.8) находим доверительный интервал
 ;
;
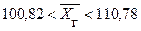 .
.
Оценка истинного значения измеряемой величины.
Пусть производится 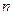 независимых равноточных измерений некоторой физической величины, истинное значение
независимых равноточных измерений некоторой физической величины, истинное значение 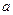 которой неизвестно. Будем рассматривать результаты отдельных измерений как случайные величины
которой неизвестно. Будем рассматривать результаты отдельных измерений как случайные величины  . Эти величины независимы (измерения независимы), имеют одно и то же математическое ожидание
. Эти величины независимы (измерения независимы), имеют одно и то же математическое ожидание 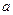 (истинное значение измеряемой величины), одинаковые дисперсии
(истинное значение измеряемой величины), одинаковые дисперсии 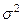 (измерения равноточны) и распределены нормально (такое допущение подтверждается опытом). Таким образом, все предположения, сделанные при выводе доверительных интервалов в § 2 – 4, выполняются и, следовательно, можно использовать полученные в них формулы. То есть, истинное значение измеряемой величины можно оценивать по среднему арифметическому результатов отдельных измерений при помощи доверительных интервалов. Поскольку обычно
(измерения равноточны) и распределены нормально (такое допущение подтверждается опытом). Таким образом, все предположения, сделанные при выводе доверительных интервалов в § 2 – 4, выполняются и, следовательно, можно использовать полученные в них формулы. То есть, истинное значение измеряемой величины можно оценивать по среднему арифметическому результатов отдельных измерений при помощи доверительных интервалов. Поскольку обычно 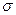 неизвестно, следует пользоваться формулами (13.5) и (13.9).
неизвестно, следует пользоваться формулами (13.5) и (13.9).
Доверительные интервалы для оценки среднего квадратического отклонения 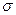 нормального распределения.
нормального распределения.
Пусть количественный признак 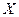 генеральной совокупности распределен нормально. Требуется оценить неизвестное генеральное среднее квадратическое отклонение
генеральной совокупности распределен нормально. Требуется оценить неизвестное генеральное среднее квадратическое отклонение 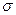 по исправленному выборочному среднему квадратическому отклонению
по исправленному выборочному среднему квадратическому отклонению 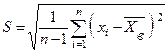 . Найдем доверительные интервалы, покрывающие параметр
. Найдем доверительные интервалы, покрывающие параметр 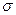 с заданной надежностью
с заданной надежностью 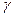 .
.
Потребуем, чтобы выполнялось соотношение
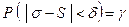
или
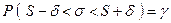 .
.
Преобразуем двойное неравенство 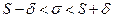 в равносильное
в равносильное
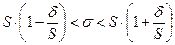 .
.
Положив  , получим
, получим
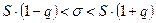 . (10)
. (10)
Необходимо найти 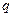 . С этой целью введем в рассмотрение случайную величину
. С этой целью введем в рассмотрение случайную величину
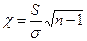 ,
,
где 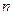 – объем выборки.
– объем выборки.
Дифференциальная функция распределения 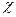 имеет вид
имеет вид
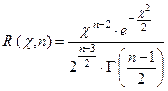 ,
,
Видно, что это распределение не зависит от оцениваемого параметра 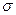 , а зависит только от объема выборки
, а зависит только от объема выборки 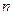 .
.
Преобразуем неравенство (10) так, чтобы оно приняло вид
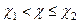 .
.
Вероятность этого неравенства равна заданной надежности 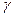 , то есть
, то есть
 .
.
Предполагая, что 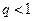 , перепишем неравенство (10) в виде
, перепишем неравенство (10) в виде
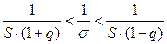 .
.
Умножив все члены неравенства на 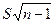 , получим
, получим
 ,
,
или
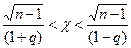 .
.
Вероятность того, что то неравенство, а следовательно, и равносильное ему неравенство (10) будет выполнено, равна
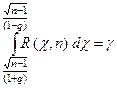 .
.
Из полученного уравнения можно по заданным 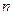 и
и 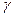 найти
найти 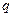 . Практически для отыскания
. Практически для отыскания 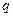 пользуются таблицей.
пользуются таблицей.
Вычислив по выборке 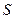 и найдя по таблице
и найдя по таблице 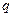 , получим искомый доверительный интервал (13.10), покрывающий
, получим искомый доверительный интервал (13.10), покрывающий 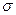 с заданной надежностью
с заданной надежностью 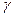 .
.
Замечание. Выше предполагалось, что 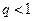 . Если
. Если 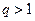 , то неравенство (10) примет вид (учитывая, что
, то неравенство (10) примет вид (учитывая, что 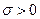 )
)
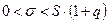 . (11)
. (11)
Доверительные интервалы для оценки дисперсии  и среднего квадратического отклонения
и среднего квадратического отклонения 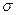 нормального распределения.
нормального распределения.
Пусть количественный признак 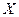 генеральной совокупности распределен нормально. Доверительный интервал для параметра
генеральной совокупности распределен нормально. Доверительный интервал для параметра  имеет вид
имеет вид
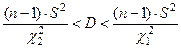 . (12)
. (12)
а для параметра 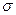 соответственно
соответственно
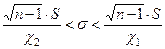 . (13)
. (13)
Значения величин 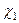 и
и 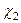 находятся по таблице значений
находятся по таблице значений 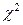 - распределения согласно равенствам
- распределения согласно равенствам
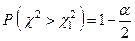 , (14)
, (14)
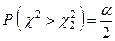 , (15)
, (15)
где 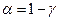 . Следует учитывать, что случайная величина
. Следует учитывать, что случайная величина 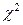 имеет
имеет 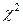 - распределение с
- распределение с 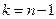 степенью свободы.
степенью свободы.
Пример. Проверена партия однотипных телевизоров 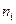 на чувствительность к видеопрограммам
на чувствительность к видеопрограммам 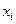 . Данные проверки представлены дискретным статистическим рядом распределения
. Данные проверки представлены дискретным статистическим рядом распределения
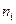
| 2 | 5 | 6 | 7 | 5 | 2 | 2 | 1 |
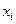 , мкв , мкв
| 200 | 250 | 300 | 350 | 400 | 450 | 500 | 550 |
С надежностью 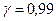 построить доверительные интервалы для
построить доверительные интервалы для 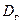 и
и 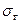 .
.
Решение. Для построения доверительных интервалов необходимо найти значения 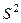 и
и  . Вычислим значение
. Вычислим значение 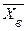 и
и 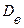
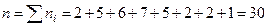 .
.
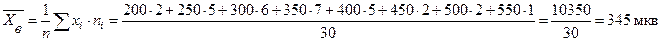 .
.
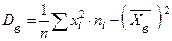 ;
;
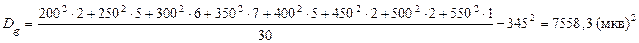 .
.
Находим исправленную дисперсию и исправленное среднее квадратическое отклонение
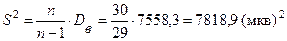 .
.
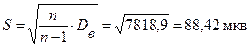 .
.
Так как 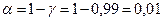 , то согласно (14) и (15) имеем
, то согласно (14) и (15) имеем
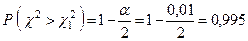 .
.
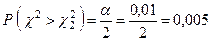 .
.
По таблице 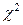 - распределения находим
- распределения находим
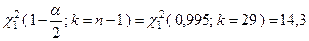 .
.

По формулам (12) и (13) искомые доверительные интервалы
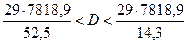 ;
;
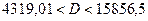 .
.
и
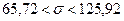 .
.
Дата добавления: 2020-11-27; просмотров: 164; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
