Эмпирический коэффициент асимметрии
Лекция 2. Вероятностное описание событий и процессов. Статистическая обработка экспериментальных данных. Оценивание показателей систем и определение их точности методами математической статистики.
Математическая статистика – это раздел математики, в котором изучаются методы обработки и анализа экспериментальных данных с помощью аппарата теории вероятностей.
Статистической совокупностью называют совокупность предметов или явлений, объединённых каким – либо общим признаком.
Результатом наблюдений над статистической совокупностью являются статистические данные. Обработка статистических данных методами математической статистики приводит к установлению определенных закономерностей, присущих массовым явлениям.
Генеральной совокупностью называется совокупность объектов или явлений, все элементы которой подлежат изучению при статистическом анализе.
В математической статистике генеральная совокупность понимается как совокупность всех мысленных наблюдений, которые могли быть произведены при выполнении данного комплекса условий. Изучение всей генеральной совокупности часто оказывается невозможным, в таком случае рассматривают некоторую часть объёма.
То есть, генеральная совокупность - это множество каких – либо однородных элементов, из которого по определенному правилу выделяется некоторое подмножество – выборка.
|
|
|
Выборочной совокупностью (выборкой) называют множество результатов наблюдений, случайно отобранных из генеральной совокупности. Выборка (случайная) обозначается X = (X1, X2,… Xn).
Таким образом, выборка представляет собой совокупный результат n независимых наблюдений над некоторой генеральной случайной величиной X.
Величина n– (количество проведенных измерений или наблюдений) называется объёмом выборки.
С точки зрения теории вероятностей, выборка – это n -мерный случайный вектор с одинаково распределёнными независимыми компонентами.
Любая конкретная выборка x = (x1, x2,… xn) (её также называют простой выборкой) есть реализация этой совокупности случайных величин.
Выборочное пространство – это пространство, состоящее из реализаций вектора X:
א = {x = (x1, x2,…xn)},
где xi – выборочное наблюдение (i = 1, 2,…n).
Таким образом, понятия выборочного пространства и генеральной совокупности совпадают.
Информация о генеральной совокупности, полученная на основе выборки, всегда будет обладать некоторой погрешностью, так как основывается на изучении только части объектов. Это выдвигает требования к отбору части объектов – выборка должна быть репрезентативной, то есть правильно отражать пропорции генеральной совокупности. Теоретически репрезентативность достигается случайностью отбора, но на практике зачастую прибегают к различным приемам неслучайного отбора. Основой математической статистики будет простая случайная выборка.
|
|
|
Характеристики (параметры) генеральной совокупности, оцененные с помощью выборки, называют выборочными характеристиками, и они, естественно, являются случайными величинами как функции от случайной выборки.
Задачи математической статистики состоят в обоснованном суждении об объективных свойствах генеральной совокупности по результатам случайной выборки (по значениям выборочных характеристик). Решение таких задач требует знания законов распределения выборочных характеристик.
На первом этапе статистической обработки производят ранжирование, то есть упорядочение данных. Упорядоченные по возрастанию числовых значений элементы выборки называют вариационным рядом X (1)≤ X(2)≤ …≤ X(n) .
Члены вариационного ряда называют порядковыми статистиками.
Крайние члены: X(1)= Xmin и X(n) = Xmax называют экстремальными значениями вариационного ряда.
Разность X(n)– X(1)= Xmax – Xmin называют размахом выборки.
|
|
|
Промежуток между экстремальными значениями вариационного ряда (X(1), X(n)) называют интервалом варьирования.
Если выборочные наблюдения в простой выборке представить в порядке неубывания числовых значений, то получится реализация вариационного ряда х(1) ≤ х(2) ≤ …≤ х( n ) .
При статистическом анализе дискретных случайных величин используют простую таблицу частот.
Если выборка содержит m £ n различных значений и значение х(i) встречается ni раз, тогда ni называется частотой, а сам неповторяющейся элемент вариационного рядах(i) – варианта.
Если для каждой варианты х(i) указать частоту её появления ni, то множество пар (х(i), ni) называется статистическим рядом.
Статистический ряд для дискретной случайной величины записывают в виде простой таблицы частот.
| № | значения | частоты |
| 1 | x min | n1 |
| … | … | … |
| m | x max | nm |
Очевидно, что сумма всех частот равна объёму выборки:
.
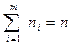Если генеральная случайная величина – непрерывная, то её интервал варьированияразбивают на небольшие интервалы, проводя группировку выборочных данных.
Число интервалов группировки m рассчитывают по формуле Стерджеса:
m » 1 + 1,4× lnn ,
|
|
|
тогда ширина (или величина) интервала равна
D =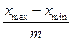 
,
где в числителе дроби стоитвариационный размах; xmax– значение Xmax; xmin – значение Xmin .
Сгруппированные данные записывают в виде таблицы:
| № интервала | Интервал | Частоты |
| 1 | (x min , x min + D) | n1 |
| 2 | (x min + D, x min + 2×D) | n2 |
| … | … | … |
| m | (x max – D x max) | nm |
Частота ni – количество данных, попавших в интервал. Таблицу такого вида называют интервальной. Иногда в интервальной таблице также указывают середины интервалов группировки.
Для графического изображения (представления) выборочных данных используют следующие характеристики: эмпирическую функцию распределения, гистограмму и полигон.
Эмпирическая функция распределения имеет вид: Fn(x) =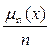 
, где m n(x) – число элементов выборки, оказавшихся меньше x ( – накопленная частота).
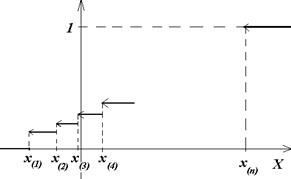
Для построения эмпирической функции распределения нанесём на ось OX члены вариационного ряда, затем построим ступенчатую функцию. Высота каждой ступеньки =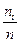 
.
На основе теоремы Бернулли для эмпирической функции распределения можно доказать следующую теорему. Теорема Гливенко: для любого действительного числа xверно:
Fn(x)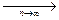 
F(x),
где F(x) – теоретическая функция распределения, Fn(x)– эмпиричес-кая функция распределения. (В утверждении теоремы имеется в виду поточечная сходимость последовательности функций).
Теорема Колмогорова: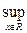 
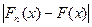= 0(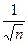 
).
То есть, если вокруг эмпирической функции распределения построить узкую зону, то с большой вероятностью можно утверждать, что функция распределения будет лежать в этой зоне.
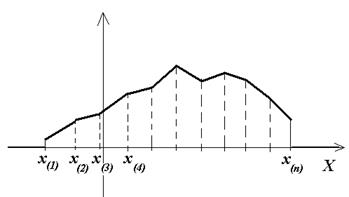Полигон частот – представляет собой ломаную, концы отрезков прямой имеют координаты (xi; 
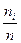). Полигон, как правило, служит для графического представления дискретного вариационного ряда. Для интервального ряда тоже строят полигон, только его ломанная проходит через точки, абсциссы которых являются серединами интервалов группировки.
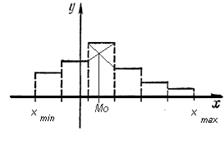
Гистограмма. При построении гистограммы используются сгруппированные данные. По оси OXоткладывают интервалы шириной D от х min до х max. На каждом интервале строят прямоугольник площадью pi = 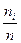(равной относительной частоте попадания в данный интервал), то есть, высота прямоугольника hi = 
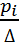.Объединение этих прямоугольников называется гистограммой выборки. Таким образом, площадь каждого прямоугольника гистограммы равна его частоте, а общая площадь равна единице.
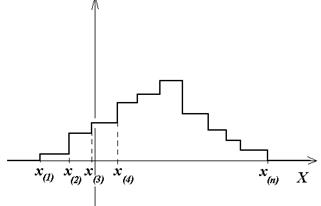
С увеличением объема выборки n и уменьшением длины интервала k гистограмма будет приближаться к кривой плотности распределения, поэтому гистограмму используют в качестве оценки для плотности распределения.
Вариационный ряд содержит достаточно полную информацию о генеральной случайной величине X, однако обилие числовых данных, с помощью которых он задаётся, усложняет их использование. На практике достаточно часто оказывается достаточным знание лишь сводных характеристик вариационного ряда: выборочных моментов, моды, медианы, асимметрии и эксцесса.
Расчёт статистических характеристик представляет собой второй после группировки данных этап обработки результатов наблюдений. Рассмотрим основные характеристики.
Выборочная (эмпирическая) средняя: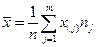 
,
где m – число интервалов группировки, x(j)– соответствующее значение варианты для дискретного случая или середина интервала группировки для непрерывного, nj – соответствующая частота. В частном случае, когда выборка содержит n различных значений (количество значений равно объёму выборки), все частоты nj = 1 и формула для выборочного среднего примет более простой вид: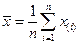 
.
Выборочная медиана – значение признака, приходящееся на середину вариационного ряда:
Медиану, как меру средней величины, используют в том случае, если крайние члены вариационного ряда по сравнению с остальными, оказались чрезмерно большими или малыми.
Выборочная мода – выборочное значение, которому соответствует наибольшая частота.
Моду можно найти по простой или интервальной таблице частот.
Моду легко найти графическим путем с помощью гистограммы.
Выборочная дисперсия: S2 =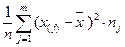 
.
Для практических вычислений S2 более удобной является следующая формула:
S2 =`x2 – (`x)2
(выборочная дисперсия равна разности среднего квадрата и квадрата выборочного среднего), где
.
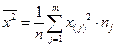Выборочное среднеквадратическое отклонение есть арифметический квадратный корень из дисперсии S.
Эмпирический коэффициент асимметрии
.
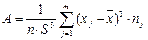Если A = 0, то распределение имеет симметричную форму.
При A > 0 говорят о положительной (или правосторонней) асимметрии.
При A < 0 говорят о отрицательной (или левосторонней) асимметрии.
Эмпирический эксцесс
.
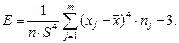Если E > 0, то полигон вариационного ряда имеет более крутую вершину по сравнению с нормальной (гауссовой) кривой.
Если E < 0, то полигон вариационного ряда имеет более пологую вершину по сравнению с нормальной (гауссовой) кривой.
Дата добавления: 2020-11-27; просмотров: 145; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!