Параллельность прямой и плоскости
Тема: Решение задач по теме: «Аксиомы стереометрии. Некоторые следствия из аксиом».
Дата: 30.10.2020 г.
Группа: ПЦ-265
Цель урока: систематизировать теоретические знания по теме: «Аксиомы стереометрии. Некоторые следствия из аксиом»; совершенствовать навыки решения задач по данной теме.
Студенты должны знать: понятия стереометрия, аксиомы стереометрии, следствия из аксиом.
Студенты должны уметь: вычислять площадь боковой поверхности цилиндра и конуса; вычислять площадь поверхности шара, вычислять площадь полной поверхности цилиндра и конуса, применять теоретический материал при решении задач по теме.
1. Актуализация опорных знаний:
Стереометрия— это раздел геометрии, в котором изучаются свойства фигур в пространстве. Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.
Простейшие фигуры в пространстве: точка, прямая, плоскость.
Плоскость.
Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.
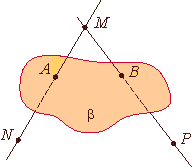На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д. Точки А и В лежат в плоскости β (плоскость β проходит
|
|
|
через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко
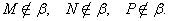это записывают так: А ∈ β, B ∈ β,
Аксиомы стереометрии и их следствия
| Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. | 
|
| Аксиома 2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую). | 
|
| Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются. |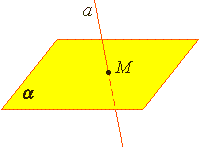 
|
| Аксиома 3. Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. В таком случае говорят, плоскости пересекаются по прямой. Пример: пересечение двух смежных стен, стены и потолка комнаты. |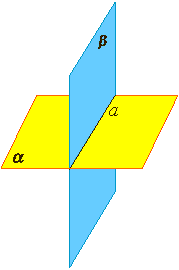 
|
| Теорема 1. Через прямую a и не лежащую на ней точку А проходит плоскость, и притом только одна. |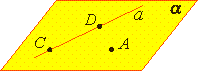 
|
| Теорема 2. Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна. |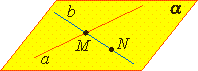 
|
Некоторые следствия из аксиом
|
|
|
Параллельные прямые в пространстве
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
| Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна. |
|
| Лемма о пересечении плоскости параллельными прямыми. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость. |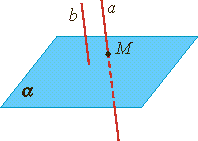 
|
| Теорема о трех прямых в пространстве. Если две прямые параллельны третьей прямой, то они параллельны (если a∥c и b∥c, то a∥b). |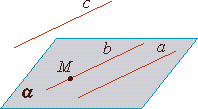 
|
Параллельность прямой и плоскости
Прямая и плоскость называются параллельными, если они не имеют общих точек.
| Признак параллельности прямой и плоскости Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости. | 
|
| Теорема. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. Теорема. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости. |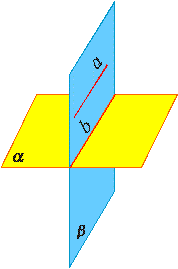 
|
Взаимное расположение прямых в пространстве
|
|
|
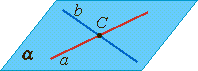
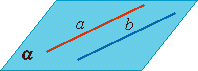
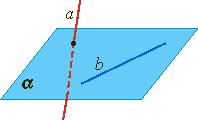
| Пересекающиеся прямые: лежат в одной плоскости, имеют одну общую точку. | Параллельные прямые: лежат в одной плоскости, не имеют общих точек (не пересекаются) | Скрещивающиеся прямые: не лежат в одной плоскости, не имеют общих точек (не пересекаются) |
| Параллельность плоскостей Две плоскости называются параллельными, если они не пересекаются, т.е. не имеют ни одной общей точки. α∥β. |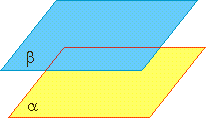 
|
| Признак параллельности двух плоскостей Теорема. Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости , то эти плоскости параллельны. Если а∥а1 и b∥b1, то α∥β. |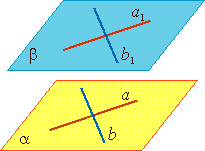 
|
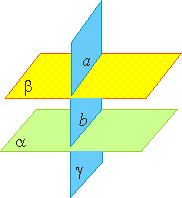Если α∥β и они пересекаются с γ, то а∥b.
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
| 
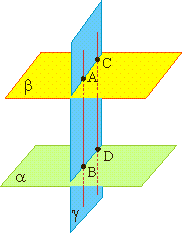Если α∥β и AB∥CD, то АВ = CD. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
|
Свойства параллельных плоскостей
|
|
|
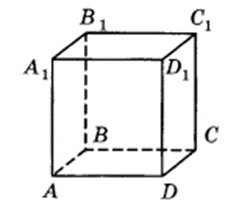№1. (устно) Прямая MN пересекает плоскость:
1) (АА1В1); 2) (ABC); 3) (AA1D1)? Разбор решения:
Внимательно рассмотрите рисунок, как вы видите прямая MN пересекает плоскости ABC и A1B1С1, рассмотрим варианты ответов, среди них есть вариант 2) (ABC), он и является верным.
Ответ: 2) (ABC);
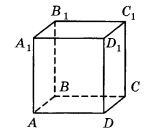№2. (устно) Пользуясь данным рисунком назовите три плоскости, содержащие прямую DС1
Решение: Внимательно рассмотрите прилагающийся рисунок, определите, где на нем располагается прямая DС1, как вы видите из рисунка он располагается в плоскостях:1)DD1С1С; 2)D1С1С; 3) DСС1. Их и запишем в ответ.
Ответ: 1)DD1С1С; 2)D1С1С; 3) DСС1
Решение задач
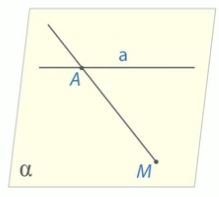1) Дана прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие через данную точку и пересекающие данную прямую, лежат в одной плоскости.
Решение: Нам дана прямая а и некоторая точка М, которая не лежит на этой прямой. Нам нужно доказать, что все прямые, которые проходят через точку М и пересекают прямую а лежат в некоторой единственной плоскости.
Мы знаем, что в силу 1 теоремы через прямую а и точку М проходит единственная плоскость, обозначим через. Теперь возьмем произвольную прямую, которая проходит через точку М и пересекает прямую а, например, в точке А. Прямая МА лежит в плоскости , потому что две ее точки М и А, лежат в этой плоскости. Значит, и вся прямая лежит в плоскости, в силу 2 аксиомы.
Итак, мы взяли произвольную прямую, которая удовлетворяет условиям задачи, и доказали, что она лежит в плоскости. Значит, все прямые, проходящие через точку М и пересекающие прямую а лежат в плоскости, что и требовалось доказать.
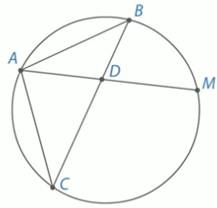2) Верно ли утверждение: а) если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости; б) если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости?
Решение:
а) Пусть дана окружность и точки А, В, С. В случае если только две точки В и С принадлежат некоторой плоскости, то совсем необязательно, что и любая другая точка окружности лежит в этой плоскости. Поэтому, данное утверждение неверно. Ответ: нет.
б) Даны три точки окружности А, В, и С. В силу аксиомы 1, через эти три различные точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. Назовем эту плоскость.
Теперь докажем, что любая точка М окружности лежит в плоскости. Соединим М с А, получим точку D. Вся прямая АD лежит в плоскости, потому что две ее точки А и D лежат в плоскости. Значит, и точка М окружности лежит в плоскости. Значит, данное утверждение верно.
Ответ: да.
3) Точки А, В, С и D не лежат в одной плоскости. а) Могут ли какие-то три из них лежать на одной прямой? б) Могут ли прямые АВ и СD пересекаться?
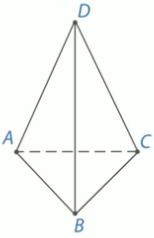Решение: а) Предположим, что любые три точки, например, А, В, С лежат на одной прямой. Тогда через эту прямую и точку D проходит плоскость, и все 4 точки лежат в этой плоскости, что противоречит условию; Ответ: нет.
б) Нет, так как через пересекающиеся прямые можно провести плоскость, а тогда, в этой плоскости содержатся все 4 точки, что противоречит условию.
Ответ: нет.
4) Через 3 точки, если они не лежат на одной прямой, можно провести плоскость, и притом только одну, в силу аксиомы А1. Ответ: да.
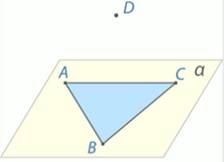б) Верно ли, что любые 4 точки лежат в одной плоскости?
Через 3 точки можно провести плоскость, а 4 точку можно взять и в этой плоскости, и вне нее. Значит, ответ отрицательный.
Ответ: нет.
в) Верно ли, что любые 4 точки не лежат в одной плоскости?
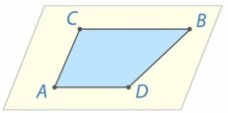Приведем конкретный пример. Рассмотрим плоский четырехугольник, в плоскости этого четырехугольника лежат 4 точки. Итак, ответ на этот вопрос отрицательный, нет. Ответ: нет.
г) Верно ли, что через любые 3 точки проходит плоскость, и притом только одна?
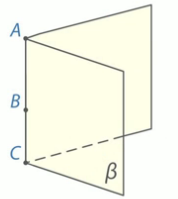Приведем пример. Возьмем 3 точки А, В, С, лежащие на одной прямой. Через них можно провести плоскость, плоскость. Через 3 точки, лежащие на одной прямой, можно провести бесконечное количество плоскостей.
Ответ: нет
Домашнее задание
Критерии оценивания:
Оценка «отлично» - выставляется обучающемуся, если правильно решены все задания, выполнены в полной мере, изложены логично.
Оценка «хорошо» - выставляется обучающемуся, если допущены незначительные погрешности в задании.
Оценка «удовлетворительно» - выставляется обучающемуся, если ответ на вопрос нелогичный, не полный.
Оценка «неудовлетворительно» - выставляется обучающемуся, если задания не решены.
ВНИМАНИЕ!!!
Уважаемые студенты, практическое задание необходимо выполнить в рабочей тетради (сфотографировать) или в формате Документа Word. Отправлять для проверки в личные сообщения на страницу ВКонтакте: https://vk.com/kolomiyetssg?z=photo95751036_324720501%2Falbum95751036_0%2Frev
Преподаватель: Коломиец Светлана Григорьевна
Дата добавления: 2020-11-23; просмотров: 125; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!