Задания самостоятельной работы.
Практическая работа № 15
Тема: «Нахождение неопределенных интегралов методом непосредственного интегрирования и методом введения новой переменной»
Цели:
· закрепить и систематизировать теоретические знания,
· формировать умения и навыки решения задач по нахождению неопределённого интеграла методом непосредственного интегрирования и методом введения новой переменной.
В результате выполнения работы студент должен знать определение, свойства и табличные данные неопределённого интеграла.
Должен уметь находить неопределённый интеграл методом непосредственного интегрирования.
План выполнения практической работы
1. Повторение основных теоретических сведений по данной теме
2. Изучение методических рекомендаций по решению задач и выполнение упражнений и задач.
3. Выполнение практической самостоятельной работы по вариантам.
4. Письменные ответы на контрольные вопросы
Задания для практической работы .
Краткие теоретические сведения.
1.3 Таблица неопределенных интегралов
Каждая из нижеследующих формул верна на каждом промежутке, принадлежащем области определения подынтегральной функции:
1 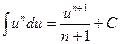
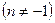 .
.
2 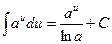
 .
.
3 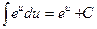 .
.
4  .
.
5  .
.
6  .
.
7  ,
,  ,
, 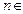
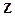 .
.
8  ,
, 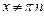 ,
, 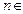
 ..
..
9 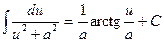 ,
, 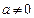 .
.
10 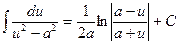 ,
, 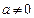 .
.
11 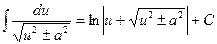 ,
,  ,
, 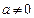 .
.
12 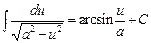 ,
, 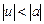 ,
, 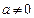 .
.
13 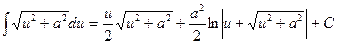 ,
, 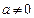
14 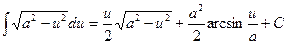 ,
, 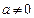
Простейшие свойства неопределенного интеграла, которые позволят интегрировать не только основные элементарные функции.
|
|
|
1. Производная от неопределенного интеграла равна подынтегральной функции:

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению:

3. Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной:

4. Постоянный множитель можно выносить за знак интеграла:
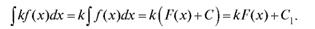
5. Интеграл от суммы или разности двух функций равен сумме или разности интегралов от этих функций:
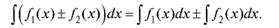
6. Формула интегрирования остается справедливой, если переменная интегрирования является функцией: если  то
то
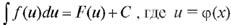 - произвольная функция, имеющая непрерывную производную. Это свойство называется инвариантностью.
- произвольная функция, имеющая непрерывную производную. Это свойство называется инвариантностью.
Метод замены переменной
Существуют две формулы замены переменной в неопределенном интеграле:
1) 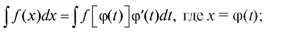 2)
2) 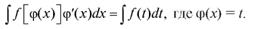
Здесь 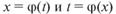 суть монотонные дифференцируемые функции своих переменных.
суть монотонные дифференцируемые функции своих переменных.
Искусство применения метода состоит, в основном, в выборе функций  так, чтобы новые интегралы являлись табличными или сводились к ним. В окончательном ответе следует вернуться к старой переменной.
так, чтобы новые интегралы являлись табличными или сводились к ним. В окончательном ответе следует вернуться к старой переменной.
Заметим, что подведение под знак дифференциала является частным случаем замены переменной.
|
|
|
Методические рекомендации по решению упражнений и задач.
Пример 1.

Решение. Здесь следует ввести новую переменную t так, чтобы избавиться от квадратного корня. Положим x + 1 = t, тогда x = t2 + 1, а dx = 2tdt:

Пример 2.

Решение. Заменив x - 2 на t, получим в знаменателе одночлен и после почленного деления интеграл сведется к табличному от степенной функции:

2. Используя основные правила интегрирования и таблицу интегралов, найдите следующие неопределенные интегралы:
а)  ; б)
; б) 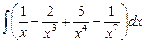 ; в)
; в)  ; г)
; г) 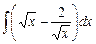 ;
;
Задания самостоятельной работы.
1 вариант
Найдите следующие неопределенные интегралы:
1) 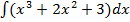 ;
2) ;
2) 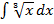 ;
3) ;
3)  ;
4) ;
4) 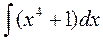 ;
5) ;
5) 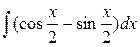 ;
6) ;
6)  Найти неопределенные интегралы методом подстановки.
1.
Найти неопределенные интегралы методом подстановки.
1. 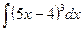 .
2. .
2. 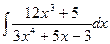
| 2 вариант
Найдите следующие неопределенные интегралы:
1) 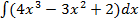 ;
2) ;
2) 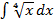 ;
3) ;
3) 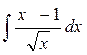 4)
4) 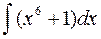 ;
5) ;
5) 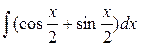 6)
6) 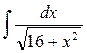 Найти неопределенные интегралы методом подстановки.
1.
Найти неопределенные интегралы методом подстановки.
1. 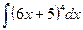 .
2. .
2. 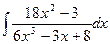 . .
|
3 вариант
Найдите следующие неопределенные интегралы:
1) 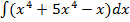 ;
2) ;
2) 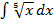 ;
3) ;
3) 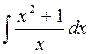 ;
4) ;
4) 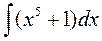 ;
5) ;
5)  ;
6) ;
6) 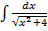 Найти неопределенные интегралы методом подстановки.
1.
Найти неопределенные интегралы методом подстановки.
1. 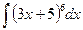 .
2. .
2. 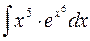 . .
| 4 вариант
Найдите следующие неопределенные интегралы:
1) 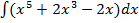 ;
2) ;
2) 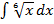 ;
3) ;
3) 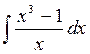 ;
4) ;
4) 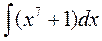 ;
5) ;
5) 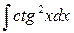 ;
6) ;
6) 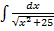 Найти неопределенные интегралы методом подстановки.
1.
Найти неопределенные интегралы методом подстановки.
1. 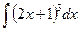 .
2. .
2.  . .
|
Контрольные вопросы
|
|
|
1) Что называется неопределённым интегралом?
2) В чём состоит геометрический смысл неопределенного интеграла?
3) Свойства неопределенного интеграла?
4) Какие методы нахождения неопределённых интегралов вы освоили?
5) В чём суть метода замены переменной?
Дата добавления: 2020-11-23; просмотров: 140; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
