VI. Более сложные задачи. Задачи ЕГЭ разных лет.

Геометрическая прогрессия

Ребята! Сегодня мы с вами повторяем такую важную тему, как геометрическая прогрессия. С прогрессией человечество на практике встречалось постоянно, и достаточно часто, в неблагоприятных ситуациях.

Например, обычные домовые или полевые мыши, уничтожающие урожай, за год приносят 5-10 приплодов по 3-12 детёнышей в каждом, половой зрелости они достигают через месяц после рождения, а беременность длится 19—21 день. Таким образом, от одной пары получаем 100 детенышей. Одна мышь съедает 3 грамма зерна в сутки, а портит в 10 раз больше. Попробуйте подсчитать сколько зерна перепортит и съест полсотни мышек, запертых в амбаре и защищенных его стенами от хищников. Мыши нередко становились причиной голода, от которого вымирали селения.

От чумы, оспы и других болезней умирало семь- девять человек из 10.Наиболее массовую смертность пандемия чумы принесла в средине XIV века, прокатившись по всей Евразии и унеся по самым скромным подсчетам историков жизни 60 млн. человек. Во все последующие века также наблюдались крупные вспышки чумы, последняя из которых была отмечена в 1910-1911 годах в северо-восточной части Китая.

Эти и многие другие процессы описываются геометрической прогрессией. Но нельзя связывать прогрессию только с неблагоприятными ситуациями. Например, при денежных вкладах в банк, полученная в итоге сумма рассчитывается именно геометрической прогрессией. Результаты рекламной компании (как и слухи) распространяется в обществе именно по такому правилу.

Первый и второй блок содержат теоретический материал по теме, знание которого обязательно. Изучите его и при необходимости обратитесь к видеоурокам.

В третьем и четвертом блоках вашему вниманию предлагаются задачи, направленные на повторение и отработку основных формул. Для этого предназначены задачи группы 1-5. Решать их необходимо только в том случае, если рассмотрение решений разобранных задач вызывает затруднения. Подобные задания входили в ОГЭ первая часть.

Пятый блок содержит задачи, описывающие реальные жизненные ситуации, а также исторические задачи. Они входили в олимпиады разных лет.

Задачи шестого блока предназначены для решения на этом занятии, решения и ответы высылайте на электронную почту ddut_maths@rambler.ru.

Телефон для связи +79211396057

Группы 6 - 7. Похожие задачи размещены в ЕГЭ – задание 11

Группа 8. Похожие задачи размещены в ЕГЭ – задания 19, 18.

I. Повторите необходимую теорию и формулы по теме.

Основная теория и формулы

Определение: Геометрической прогрессией называют числовую последовательность 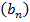, каждый следующий член которой получается из предыдущего умножением его на постоянное число, не равное нулю.

Это число называют знаменателем геометрической прогрессии и обозначают буквой q.

Например , последовательность 33; 66; 1212; 2424; 4848… является геометрической прогрессией, потому что каждый следующий элемент отличается от предыдущего в два раза (иначе говоря, может быть получен из предыдущего умножением его на два):

Как и любую последовательность, геометрическую прогрессию обозначают маленькой латинской буквой. Числа, образующие прогрессию, называют ее членами (или элементами). Их обозначают той же буквой, что и геометрическую прогрессию, но с числовым индексом, равным номеру элемента по порядку.

Если в геометрической прогрессии (b_n) известен первый член b₁ и знаменатель q, то возможно найти любой член прогрессии.

b₂=b₁⋅q;

b₃=b₂⋅q=b₁⋅q⋅q=b₁⋅q²;

b₄=b₁⋅q³

и т. д.

Общий член геометрической прогрессии b_n можно вычислить, используя формулу:

b_n = b₁⋅qⁿ⁻¹, где

n — порядковый номер члена прогрессии,

b₁ — первый член последовательности,

q — знаменатель.

Сумма первых n членов геометрической прогрессии

Сумму первых n членов геометрической прогрессии S_nможно найти, если вычислить её члены b₁, b₂... b_n и затем их значения сложить.

Вычисляя сумму первых n членов геометрической прогрессии, удобнее использовать

1-ю формулу:

n — количество членов последовательности (порядковый номер),

b₁ — первый член последовательности,

b_n — n-ый член последовательности,

q — знаменатель.

Решая задачи, удобнее использовать 2-ю формулу: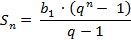

II. При необходимости изучите видеоматериал

https://www.youtube.com/watch?v=0nj5a1n0AY8 (продолжительность 6:47)

https://www.youtube.com/watch?v=j1CQ_y5BPU0 (продолжительность 5:50)

https://foxford.ru/courses/1598/lessons/34781 (продолжительность 1:19:41 )

III. Рассмотрите примеры решения некоторых примеров.

Задача 1. Выписаны первые три члена геометрической прогрессии: -5; 15; -45; …

Найдите её пятый член. Найдите сумму первых пяти её членов.

Решение:

b ₁ = - 5

b ₂ = 15

b ₃ = - 45

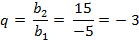
Ответ: ,

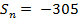
Задача 2. Геометрическая прогрессия задана условиями: 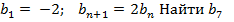и сумму первых семи её членов.

Решение:

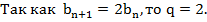Найти нужно седьмой член, тогда n= 7

Известно, что b₁= - 2, b_n = b₁⋅qⁿ⁻¹, тогда

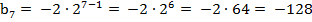Для нахождения суммы семи членов прогрессии, используем формулу
, b₁= - 2, 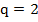, n = 7, получим:

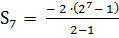Ответ: ,

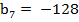
Задание 3. Геометрическая прогрессия задана условием b_n = 88∙2ⁿ. Найдите b_4.

Решение: если n = 1, то b₁ = 88∙2¹ = 88∙2 = 176,

если n = 2, то b₂ = 88∙2² = 88∙4 = 352,

если n = 3, то b₃ = 88∙2³ = 88∙8 = 704,

если n = 4, то b₄ = 88∙2⁴ = 88∙16 = 1408.

Ответ: 1408.

Задача 4. Выписано несколько последовательных членов геометрической прогрессии. Найдите член прогрессии, обозначенный буквой x.

…; 189; x; 21; …

Решение:

b ₂ = 189

b ₃ = х

b ₄ = 21

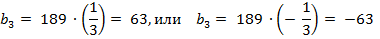
Ответ: 63 или – 63.

Геометрическая прогрессия задана условием … n n = 175 1 1) 5 æ ö ç ÷ è ø b - × - . Найдите . b4 n n 2) b =51,5 2 × -( ) . Найдите . b4 n n 3) b =64,5 2 × -( ) . Найдите .

Задача 5. В геометрической прогрессии сумма первого и второго членов равна 144, а сумма второго и третьего членов равна 48. Найдите первые три члена этой прогрессии

Решение: Запишем условие задачи в виде системы уравнений:

Используя формулы b₂=b₁⋅q; b₃= b₁⋅q⋅q=b₁⋅q², получим

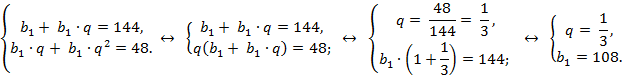
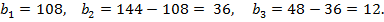
Ответ: 108, 36, 12, …

IV. Задачи для самостоятельного решения

Группа 1. Выписаны первые три члена геометрической прогрессии:

1) −84; 42; −21; … Найдите её пятый член. Найдите сумму первых пяти её членов.

2) −175; −140; −112; … Найдите её пятый член. Найдите сумму первых пяти её членов.

3) −250; 150; −90; … Найдите её пятый член. Найдите сумму первых пяти её членов.

4) 7; 14; 28; … Найдите её пятый член. Найдите сумму первых пяти её членов.

Группа 2.

1) Геометрическая прогрессия задана условиями: 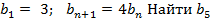и сумму первых пяти её членов.

2) Геометрическая прогрессия задана условиями: и сумму первых шести её членов.

3) Геометрическая прогрессия задана условиями: и сумму первых шести её членов.

4) Геометрическая прогрессия задана условиями: 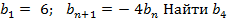и сумму первых четырех её членов.

Группа 3.1) Геометрическая прогрессия задана условием b_n = 62,5∙2ⁿ. Найдите b_4.

2) Геометрическая прогрессия задана условием b_n = 40∙( - 2)ⁿ. Найдите b_5.

3) Геометрическая прогрессия задана условием b_n = -175∙(0,2)ⁿ. Найдите b_3.

4) Геометрическая прогрессия задана условием b_n = 81 . Найдите b_3.

Группа 4. Выписано несколько последовательных членов геометрической

прогрессии. Найдите член прогрессии, обозначенный буквой x.

1) …; 162; x; 18; …

2) …; - 3; x; - 27; …

3) …; -1; x; -49; …

4) …; -6; x; - 24; …

Задача 5. В геометрической прогрессии сумма первого и второго членов равна…

1) 75, а сумма второго и третьего членов равна 150. Найдите первые три члена этой прогрессии.

2) 200, а сумма второго и третьего членов равна 50. Найдите первые три члена этой прогрессии

3) 144, а сумма второго и третьего членов равна 48. Найдите первые три члена этой

прогрессии

V. Геометрическая прогрессия в истории обмана …

Задача 1. Организатор финансовой пирамиды начинает вовлекать в свою организацию и говорит, что, если внести указанную плату по указанным адресам по 1 рублю, а затем заплатить ещё по 5 таким же адресам, вычеркнув первый адрес и дописав свой последним, то через некоторое время вы получите уйму денег. Хотя желающих разбогатеть по щучьему веленью немало, но в выигрыше оказываются только учредители такой игры. Почему?

Решение.

Дело в том, что число участников увеличивается в 5 раз с каждым кругом. Если пятёрка устроителей подпишет, допустим, 120 человек со своими адресами, то в первом круге участвуют 120 человек, во втором – 600, в третьем – 3 000, …, в десятом – 234 375 000 человек; это намного больше населения страны.

Ответ: Так что участник, включившийся в восьмом или девятом круге, уже ничего не получит.

Задача 2. Приходит как-то раз к одному богатому купцу мужик и предлагает сделку. Давай, говорит, в течение месяца я буду приносить тебе каждое утро по 100 000 руб., а ты мне взамен в первый день отдашь 1 коп., а в каждый последующий в 2 раза больше. Во второй день - 2 коп., в третий - 4 коп. и т.д.» Подумал купец и подписал договор. Кому выгодна сделка?

Решение: Сумма, которую получит купец S=100 000руб 30дней=3 000 000руб Сумма, которую получит мужик

1-ый день-1 коп

2-ой день-2 коп

3-ий день-4 коп

4-ый день-8 коп

5-ый день-16 коп

6-ой день-32 коп

7-ой день-64 коп

8-ой день-128 коп

9-ый день-256 коп

10-ый день-512 коп

11-ый день-1 024 коп

12-ый день-2 048 коп

13-ый день-4 096 коп

14-ый день-8 192 коп

15-ый день-16 384 коп

Получаем: b₁ = 1; q = 2 Найти: S₃₀ - ? Тогда S₃₀= 10 737 418 руб. 23 коп.

Купец получил – 3 000 000 р, мужик – 10 737 418 р. 23 коп., разница составляет – 7 737 418 руб. 23 коп.

Ответ: прибыль получил мужик.

…и биологии.

Задача 3. Бактерия, попав в живой организм, к концу 20-й минуты делится на две бактерии, каждая из них к концу следующих 20 минут делится опять на две и т.д. Найдите число бактерий, образующихся из одной бактерии к концу суток.

Решение:

В сутках 1 440 минут, каждые двадцать минут появляется новое поколение, то есть - за сутки 72 поколения.

По формуле суммы n первых членов геометрической прогрессии, у которой b1=1, q=2, n=72, находим, что

S72=2⁷²- 1= 4 722 366 482 869 645 213 696 - 1= 4 722 366 482 869 645 213 695.

Ответ: 4 722 366 482 869 645 213 695

VI. Более сложные задачи. Задачи ЕГЭ разных лет.

Группа 6

Задача 1. Карабас Барабас в первый год работы кукольного театра получил прибыль в размере 5000 золотых. Каждый следующий год его прибыль увеличивалась на 300% по сравнению с предыдущим годом. Сколько золотых заработал Карабас Барабас за третий год?

Решение.

Поскольку каждый год прибыль увеличивалась на 300%, она увеличивалась в 4 раза по сравнению с предыдущим годом (100% изначального дохода + 300% увеличения). Следовательно, перед нами геометрическая прогрессия.

Известно, что b₁= 5000, 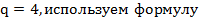b_n = b₁⋅qⁿ⁻¹, тогда

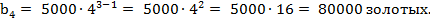
Ответ: 80000 золотых.

Группа 6. Задачи для самостоятельного решения

1) Кот Матроскин от своей коровы Мурки получил в 2000 году 5 000 литров молока. Каждый следующий год удой увеличивалась на 7% по сравнению с предыдущим годом. Сколько литров молока составил удой за 2002 год?

2) Шарик, получив в подарок фоторужье, в 1980 сделал 1400 фотографий. Каждый следующий год, по мере увеличения опыта, число сделанных им фотографий увеличивалась на 16% по сравнению с предыдущим годом. Сколько рублей фотографий сделал Шарик за 1984 год?

3) Скрудж Макдак получил в 1991 году прибыль в размере 1100000 рублей. Каждый следующий год его прибыль увеличивалась на 42% по сравнению с предыдущим годом. Сколько рублей заработал Скрудж Макдак за 1996 год?

4) Бизнесмен Бубликов получил в 2000 году прибыль в размере 1300000 рублей. Каждый следующий год его прибыль увеличивалась на 7% по сравнению с предыдущим годом. Сколько рублей заработал Бубликов за 2002 год

Задача 2. Компания "Альфа" начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 5000 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 200% от капитала предыдущего года. А компания «Бета» начала инвестировать средства в другую отрасль в 2003 году, имея капитал в размере 10000 долларов, и, начиная с 2004 года, ежегодно получала прибыль, составляющую 400% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2006 года, если прибыль из оборота не изымалась?

Решение.

Каждый год прибыль компании «Альфа» составляла 200% от капитала предыдущего года, значит, капитал каждый год составлял 300% от капитала предыдущего года q = 3. В конце 2006 года на счёте компании «Альфа» была сумма

долларов.

Каждый год прибыль компании «Бета» составила 400% от капитала предыдущего года, значит, капитал каждый год составлял 500% от капитала предыдущего года q = 5. В конце 2006 года на счёте компании «Бета» была сумма

долларов.

1 250 000 – 1 215 000 = 35 000.

Таким образом, капитал компании «Бета» был на 35 000 долларов больше.

Ответ 35 000.

. Задачи для самостоятельного решения

1) Компания "Альфа" начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 3000 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 100% от капитала предыдущего года. А компания "Бета" начала инвестировать средства в другую отрасль в 2003 году, имея капитал в размере 5000 долларов, и, начиная с 2004 года, ежегодно получала прибыль, составляющую 200% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2006 года, если прибыль из оборота не изымалась?

2) Компания "Альфа" начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 3500 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 100% от капитала предыдущего года. А компания "Бета" начала инвестировать средства в другую отрасль в 2005 году, имея капитал в размере 4000 долларов, и, начиная с 2006 года, ежегодно получала прибыль, составляющую 300% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2009 года, если прибыль из оборота не изымалась?

3) Компания "Альфа" начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 5000 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 100% от капитала предыдущего года. А компания "Бета" начала инвестировать средства в другую отрасль в 2004 году, имея капитал в размере 6000 долларов, и, начиная с 2005 года, ежегодно получала прибыль, составляющую 200% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2007 года, если прибыль из оборота не изымалась?

Группа 7

Задача 3. Дано квадратное уравнение aх² - bх + c = 0 где a, b, c — натуральные числа, не превосходящие 200. Также известно, что числа a, b и c попарно отличаются друг от друга не менее, чем на 2.

а) Может ли такое уравнение иметь корень 9?

б) Может ли такое уравнение иметь корень 135?

в) Какой наибольший целый корень может иметь такое уравнение?

Решение

а) Да, например, 2х² – 20х +18 = 0

б) Пусть уравнение aх² + bх + c = 0 имеет корень 135. Тогда a135² + bх135 + c = 0 (*) откуда

c = b135 – a135² а значит, число с кратно 135. Среди натуральных чисел, не больших 200, такое число только одно: с = 135. Подставляя в (*) вместо с число 135 и сокращая на 135, получаем a135 – b +1 = 0 откуда b = 135a + 1. Если а больше или равно 2 то b больше или равно 270, что невозможно; поэтому a = 1 и b = 136. Найденные числа b и с отличаются на 1, что противоречит условию. Таким образом, заданное уравнение не может иметь корнем число 135.

в) Рассуждая аналогично решению пункта б), докажем, что данное уравнение не может иметь целый корень, больший 100. Для этого достаточно заменить в решении пункта б) число 135 на произвольное целое число, большее 100, от этого рассуждение не изменится.

Корень, равный 100, у данного уравнения быть может: уравнение х² - 102х + 200 = 0 имеет корень 100 и полностью удовлетворяет условию задачи.

Ответ: а) да, например, б) нет; в) 100.

Задача 4. Найдите все значения параметра а, при которых множество решений неравенства содержит все члены некоторой бесконечной убывающей геометрической прогрессии с первым членом, равным 2,5, и положительным знаменателем.

Решение: Допустим, что все члены геометрической прогрессии 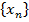с первым членом

х₁ = 2,5, и положительным знаменателем удовлетворяет неравенству:

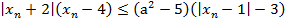Так как все члены прогрессии положительны, то можем записать:

Для х₁ = 2,5, то

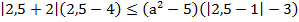
4,5 ∙(- 1,5) ≤ (а² -5)(-1,5) тогда (а² -5) ≤ 4,5 или а²≤ 9,5.

Получили необходимое условие для выполнения задачи.

Рассмотрим модуль .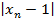

При подмодульное выражение отрицательно. Пусть 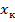первый член прогрессии, который меньше 1, тогда получаем

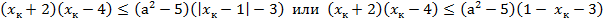
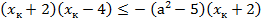
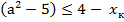
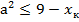
Так как первый член прогрессии и знаменатель положительны, то 0 < х < 1 и 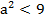, то получаем более точную оценку. Докажем, что она достаточна.

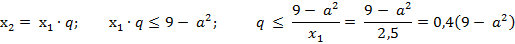
По рассмотренному выше 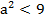, то есть 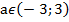. Для таких значений а найдется положительное q, удовлетворяющее неравенству.

Прогрессия убывающая, т.е. каждый член прогрессии будет меньше предыдущего, то условие 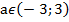можно считать не только необходимым, но и достаточным.

Ответ: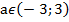
Задачи для самостоятельного решения

1) Найдите все значения параметра а, при которых множество решений неравенства 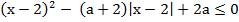содержит все члены некоторой бесконечной убывающей геометрической прогрессии с первым членом, равным 2,9, и положительным знаменателем

2) Найдите все значения параметра а, при которых множество решений неравенства 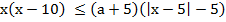содержит все члены некоторой бесконечной убывающей геометрической прогрессии с первым членом, равным 9,8, и положительным знаменателем

Ответы на задания и решения высылать на электронную почту ddut_maths@rambler.ru

Дата добавления: 2020-11-23; просмотров: 76; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!