Задачи для самостоятельного решения.
Вероятность P (A) события A «наугад кинутая точка на область G попадет в область g вычисляется по формуле
P( A) = mesg/ mesG
При этом область g называется благоприятной для события . Символом mes обозначается мера области, которая может быть длинной отрезка, площадью фигуры, объемом тела и т.п.
Задача 1. На отрезок [0;1] наудачу бросается точка. Какова вероятность того, что она попадёт в промежуток [0.4; 0.7] ?

Поскольку на отрезке бесконечно много точек, то здесь нельзя применить формулу p(A) = m/n (ввиду бесконечно большого значения «эн») и поэтому на помощь приходит другой подход, называемый геометрическим определением вероятности.
Задача 2. В прямоугольник 5*4 см2 вписан круг радиуса 1,5 см. Какова вероятность того, что точка, случайным образом поставленная в прямоугольник, окажется внутри круга?
Решение: P = Sкруга/S прямоуг = π*1,5*1,5/(4*5) = 0,353
Задача 3. Какова вероятность Вашей встречи с другом, если вы договорились встретиться в определенном месте, с 12.00 до 13.00 часов и ждете друг друга в течение 5 минут?
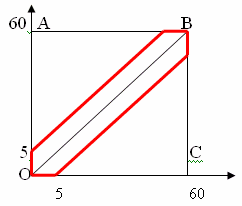
Решение: Используем геометрическое определение вероятности события A = (Встреча с другом состоится). Обозначим за х время прихода одного и у время прихода другого друга, 0≤х,у≤60 (минут). В прямоугольной системе координат этому условию удовлетворяют точки, лежащие внутри квадрата ОАВС. Друзья встретятся, если между моментами их прихода пройдет не более 5 минут, то есть y−x<5,y>x, для одного друга, и x−y<5,x>y для другого. Этим неравенствам удовлетворяют точки, лежащие в области G, очерченной красным. Тогда вероятность встречи равна отношению площадей области GG и квадрата, то есть
|
|
|
P(A) = SG/SOABC = (60⋅60−55⋅55)/60⋅60=23/144=0,16.
Ответ: 0,16
Задача 4. . На отрезке АВ длиной l независимо одна от другой поставлены 2 точки L и
M , положение каждой из которых равновозможно на AB . Найти вероятность того,
что точка L будет ближе к точке M , чем к точке A .
Решение. Используем геометрическое определение вероятности. Пусть точка L имеет координату
x, точка M имеет координату y (считаем, что A имеет координату 0, B имеет
координату т ). Точки x y, выбираются произвольно и независимо в отрезке [0; т].
Введем прямоугольную систему координат с осями Ox y, в этом случае можно считать,
что точка (x, y) выбирается произвольным образом из квадрата т × т .
Теперь найдем область этого квадрата, которая соответствует всем точкам, удовлетворяющим условию: «точка L будет ближе к точке М, чем к точке А». Это условие выполняется, если длина LM < LA, то есть |x − y |< x . Раскрываем модуль:
1) Пусть x >y , тогда получаем x− y< x, − y< 0 и y > 0. То есть, этому условию удовлетворяют все точки, лежащие в квадрате ниже прямой y= x.
|
|
|
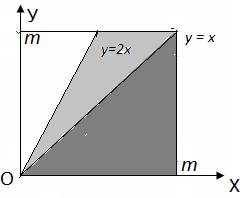
2) Пусть x< y , тогда получаем − x + y < x, y < 2x . То есть, этому условию удовлетворяют все точки, лежащие в квадрате выше прямой y= x и ниже прямой y = 2 x.
Тогда, по геометрическому определению вероятности искомая вероятность равна отношению площади заштрихованной фигуры (точки которой благоприятствуют событию) к площади всего квадрата (множество возможных значений), то есть
P = Sфигуры/Sквад = (т∙ т – 0,5т∙0,5т)/ т∙т = 0,75
Ответ 0,75
Задача 5. Метровую ленту случайным образом разрезают ножницами. Найти вероятность того, что длина обрезка составит не менее 80 см.
Решение: «чего тут сложного? Вероятность равна 1/5-й». Это автоматическая ошибка, которую допускают по небрежности. Да, совершенно верно – длина обрезка составит не менее 80 см, если от ленты отрезать не более 20 сантиметров. Но здесь часто забывают, что искомый разрез можно сделать как с одного конца ленты, так и с другого:
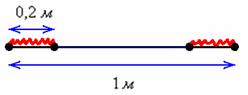
Рассмотрим событие: А – длина обрезка составит не менее 0,8 м. Поскольку ленту можно разрезать где угодно, то общему числу исходов соответствует её длина: L= 1м. Благоприятствующие событию А участки разреза отмечены на рисунке красным цветом и их суммарная длина равна: l = 0,2 + 0,2 = 0,4 м По геометрическому определению:
|
|
|
Р(А) = l/ L = 0,4 м/1 м = 0,4.
Задача 6. После бури на участке между 40-м и 70-м километрами телефонной линии произошёл обрыв провода. Какова вероятность того, что он произошёл между 50-м и 55-м километрами линии?
Решение: используем геометрическое определение вероятности. Общему числу исходов соответствует участок длиной L = 70 – 40 = 30 км, благоприятствующему количеству исходов – участок длиной l = 55 – 50 = 5 км. Таким образом: Р = l/ L = 5/30 = 1/6 – вероятность того, что обрыв провода произошёл между 50-м и 55-м километрами линии.
Ответ: 1/6
Задача 7. В треугольник со сторонами а = 9, в = 13, с = 16 вписан круг. Точка М произвольно ставится в треугольник. Найти вероятность того, что точка попадёт в круг.
Решение: поскольку точка ставится в треугольник, а круг лежит внутри, то общему числу исходов соответствует площадь треугольника, а множеству благоприятствующих исходов – площадь вписанного круга. Что тут сказать? Ищем площади:
Если даны длины сторон треугольника, то его площадь удобно найти по формуле Герона
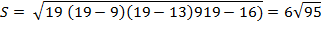
Площадь вписанного круга найдём по формуле S кр = πR2 где R = S∆/р – его радиус.
Итак, S = 180π/19. По геометрическому определению: р = Sкр/S∆ ≈0,51 – вероятность того, что точка М попадёт во вписанный круг.
|
|
|
Ответ: 0,51
Задачи для самостоятельного решения.
1. На плоскости начерчены две концентрические окружности, радиусы которых 6 и 12 см соответственно. Какова вероятность того, что точка, брошенная наудачу в большой круг, попадет в кольцо, образованное указанными окружностями?
2. В круг радиуса 5 см вписан правильный треугольник. Найти вероятность того, что точка, брошенная в этот круг, попадет в данный треугольник.
3. В шар вписана правильная треугольная пирамида. Передвигающийся по транспортной ленте шар случайно попадает под точечный луч лазера. Найти вероятность попадания точечного луча лазера в пирамиду.
4. В прямоугольник С вершинами R(-2, 0), L(-2,9), М(4, 9), N(4, 0) брошена точка. Найти вероятность того, что ее координаты будут удовлетворять неравенствам 0 ≤ y ≤ 2x − x2+8.
5. Метровый шнур случайным образом разрезают ножницами. Найти вероятность того, что длина обрезка составит не менее 80 см.
6. Машенька и Володя условились встретиться в памятника А.С. Пушкина через десять лет после окончания школы, но оба забыли точное время встречи. Тем не менее каждый из них был уверен, что второй ждет его между 12 и 13 часами дня. Пришедший первым ждет второго в течение пятнадцати минут, после чего уходит. Найти вероятность того, что Мария и Владимир встретятся, если каждый из них наудачу выбирает момент своего прихода (в промежутке от 12 до 13 часов).
Ответы на задания высылать на электронную почту ddut_maths@rambler.ru
Онлайн урок состоится в понедельник в zoom
Тема занятия «Решение задач по теории вероятностей»
Дата добавления: 2020-11-23; просмотров: 1840; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
