СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
ОПРЕДЕЛЕННЫЙ ИНТЕГРА.»
I. Определение криволинейной трапеции.
Изучая геометрию, научились находить площади фигур, границами которых являются ломаные линии, а также площадь круга и его частей.
В математике разработаны методы, позволяющие вычислять площади фигур, границами которых являются кривые линии (части парабол, гипербол, синусоид и т.д.).


 Теперь, используя знания о первообразной функции, мы научимся находить площади фигур, называемых криволинейными трапециями.
Теперь, используя знания о первообразной функции, мы научимся находить площади фигур, называемых криволинейными трапециями.
Пусть дана функция y=f(x). Рассмотрим график функции на промежутке [a; b].
ОПРЕДЕЛЕНИЕ: Криволинейной трапецией называется фигура, ограниченная отрезком [ a; b] оси 0х, прямыми х=а и х= b и графиком непрерывной и не меняющей на отрезке [ a; b] знака функции y= f( x).
II. Площадь криволинейной трапеции (I-я формула).
Рассмотрим криволинейную трапецию, ограниченную графиком функции y=f(x), прямыми х=а и х=b и отрезком [a; b] оси абсцисс.
Пусть 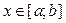 . Площадь криволинейной трапеции, заштрихованной на
. Площадь криволинейной трапеции, заштрихованной на
|
|
|
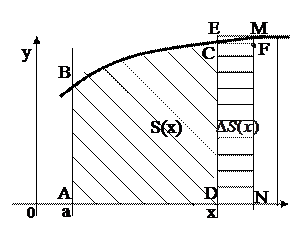
Между функцией y=f(x), одной из границ данной криволинейной трапеции и
ее площадью существует связь, которую можно записать в виде следующего равенства:
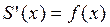
Это равенство означает, что переменная площадь S( x) есть первообразная для функции f( x). Поэтому площадь криволинейной трапеции может быть вычислена при помощи интегрирования.
|
|
|
Используя полученное равенство 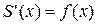 , где
, где 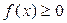 на промежутке [a; b], выведем формулу для вычисления площади криволинейной трапеции.
на промежутке [a; b], выведем формулу для вычисления площади криволинейной трапеции.
Т.к. согласно основному свойству первообразных функция имеет множество первообразных, отличающихся друг от друга постоянным слагаемым, пусть S(x) и F(x) – две первообразных функции f(x),
тогда S(x)=F(x)+C для всех 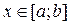 .
.
Подставив в равенство S(x)=F(x)+C вместо х число а, получим
S (a) =F (a) +C.
Но S(x) – это площадь, значит, S(a)=0, следовательно,
F (a) +C=0, C= - F (a).
Таким образом, S(x)=F(x) – F(a). Искомую площадь криволинейной трапеции получим путем подстановки в последнее равенство х=b:
S=F (b) – F (a).
III. Определенный интеграл. Формула Ньютона – Лейбница.
Выведем еще одну формулу для нахождения площади криволинейной трапеции.
 Рассмотрим положительную и непрерывную функцию
Рассмотрим положительную и непрерывную функцию
y=f(x), определенную на [a; b]
|
Разделим отрезок
[a; b] на n равных частей:
абсциссы точек деления x1 , х2 ,…,хn-1 , а соответствующие ординаты f(x1), …, f(xn-1).
Зная, что x1 - x0=x2 – x1=…=xn - xn-1=  x, и что хi – xi-1=
x, и что хi – xi-1=  обозначим
обозначим
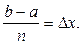
На каждом из отрезков построим прямоугольник, длина которого  х, а высота на каждом [xk-1; xk] равна f(xk-1).
х, а высота на каждом [xk-1; xk] равна f(xk-1).
|
|
|
Тогда площади каждого такого прямоугольника S=f(xk-1) 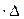 x, а площадь всей получившейся ступенчатой фигуры равна:
x, а площадь всей получившейся ступенчатой фигуры равна:
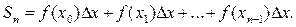
Короче эта сумма записывается так:

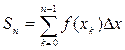 - эта интегральная сумма, где
- эта интегральная сумма, где
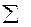 - «сигма» (греческая буква) – означает, что вычисляется сумма однотипно образованных слагаемых. Изменяя k от 0 до n-1, получим последовательно все члены рассматриваемой суммы.
- «сигма» (греческая буква) – означает, что вычисляется сумма однотипно образованных слагаемых. Изменяя k от 0 до n-1, получим последовательно все члены рассматриваемой суммы.
Очевидно, что, увеличивая n – число отрезков деления [a; b], мы уменьшаем длину каждого из них, причем эта длина стремится к нулю.
Тогда площадь ступенчатой фигуры сколь угодно близко приближается к площади данной криволинейной трапеции, т.е. существует 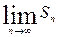 .
.
ОПРЕДЕЛЕНИЕ. Интегралом функции f( x) от а до b называется предел интегральной суммы:
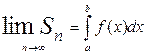 - «интеграл от а до b эф от икс де икс».
- «интеграл от а до b эф от икс де икс».
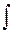 - S – «summa» - лат.;
- S – «summa» - лат.;
integer – «весь, целый» - лат. (введен в1696 г. И.Б.Бернулли)
символ 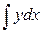 введен в 1686 г. Лейбницем;
введен в 1686 г. Лейбницем;
f(x) – подынтегральная функция;
f(x)dx ~ f(xk)  x – подынтегральное выражение
x – подынтегральное выражение
dx – дифференциал аргумента;
а – нижний предел интегрирования;
b – верхний предел интегрирования.
А теперь замечаем, что предел интегральной суммы  для неотрицательной и непрерывной на промежутке [a; b] функции f(x) равен площади соответствующей криволинейной трапеции, т.е.
для неотрицательной и непрерывной на промежутке [a; b] функции f(x) равен площади соответствующей криволинейной трапеции, т.е.
|
|
|
Sкрив.трап=  .
.
Но ранее для площади криволинейной трапеции была получена формула
Sкрив.трап=F(b) – F(a), где
F(x) – одна из первообразных функции y=f(x).
Таким образом, получим формулу:
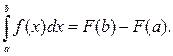 Эта формула называется формулой Ньютона-Лейбница.
Эта формула называется формулой Ньютона-Лейбница.
Замечание: Для вычисления площади криволинейной трапеции используют формулу Ньютона-Лейбница  В этой формуле:::
В этой формуле:::
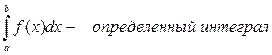 - читается - «интеграл от а до b эф от икс де икс», где .
- читается - «интеграл от а до b эф от икс де икс», где .
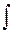 - S – «summa» - лат. – знак интеграла
- S – «summa» - лат. – знак интеграла
integer – «весь, целый» - лат. (введен в1696 г. И.Б.Бернулли)
символ 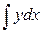 введен в 1686 г. Лейбницем;
введен в 1686 г. Лейбницем;
f(x) – подынтегральная функция;
f(x)dx – подынтегральное выражение
dx – дифференциал аргумента;
а – нижний предел интегрирования;
b – верхний предел интегрирования.
При нахождении площади криволинейной трапеции для удобства вычислений эту формулу используют в следующем виде:
Sкрив.трап= 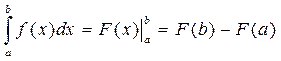 . .
|
СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
1)  ;
;
2) 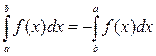 ;
;
3)  ;
;
4) если a < c < b, то 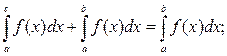
5) 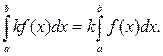
IV. Методы интегрирования определенного интеграла.
|
|
|
Замечание. Обычно рассматривают те же три наиболее применяемые метода интегрирования, которые отрабатывались при изучении неопределенного интеграла: непосредственное интегрирование, замена переменной, интегрирование по частям.
1. Метод непосредственного интегрирования – применяются свойства и таблица неопределенных интегралов, свойства определенных интегралов и формула Ньютона-Лейбница.
Пример:
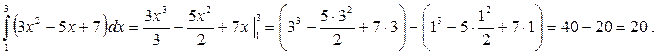
2. Метод интегрирования по частям – для определенного интегралаприменяется с использованием формулы вида 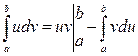 , как и для неопределенного интеграла, если под знаком интеграла стоит произведение функций.
, как и для неопределенного интеграла, если под знаком интеграла стоит произведение функций.
Примеры: 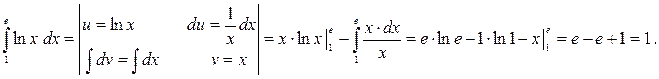
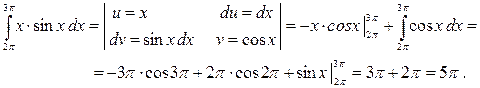
Метод замены переменной.
ТЕОРЕМА. Пусть дан интеграл 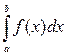 , где
, где  - непрерывная на отрезке
- непрерывная на отрезке  функция. Сделаем замену переменной
функция. Сделаем замену переменной 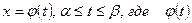 - непрерывно дифференцируемая на отрезке
- непрерывно дифференцируемая на отрезке 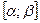 функция. Если:
функция. Если:
1). при изменении переменной 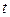 от
от 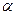 до
до 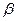 переменная
переменная  изменяется от
изменяется от  до
до 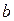 , т.е.,
, т.е.,  ;
;
2). сложная функция определена и непрерывна на отрезке 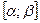 ,
,
то имеет место равенство 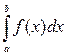 =
= 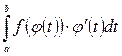 .
.
Замечание. Теорема предполагает, что, в отличие от метода замены переменной при интегрировании неопределенного интеграла, когда после интегрирования выполняли переход к старой переменной, в данном случае заменяют также и пределы интегрирования, т.е., находят  , что исключает обратный переход к старой переменной.
, что исключает обратный переход к старой переменной.
Пример:
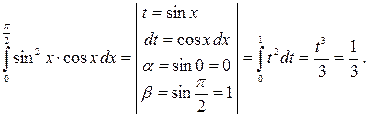
Дата добавления: 2020-11-23; просмотров: 43; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!