Свойства скалярного произведения
Занятие по математике №32 Группа 2ЖЗ Дата проведения: 30.10.20г.
Тема. Скалярное произведение векторов
Просмотреть видеофильм данной темы по ссылке: https://www.youtube.com/watch?v=dV9QjM60Qyw
Тема данного занятия: «Скалярное произведение векторов». Для вас эти слова не должны быть новыми: в планиметрии мы уже говорили о скалярном произведении. Вспомним, что скалярным произведением двух векторов на плоскости называется число, равное произведению длин данных векторов на косинус угла между ними. Также мы выводили формулу для нахождения скалярного произведения векторов в координатах: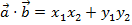 
, где 
; 
.
Угол между векторами
Введем понятие угла между векторами – оно, как и многое на этом уроке, будет абсолютно аналогичным тому, что было на плоскости.
Пусть даны два вектора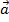 
, 
. Отложим их от некоторой точки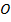 
пространства: 
; 
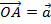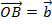. Тогда угол между векторами – это угол 
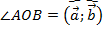. (См. Рис. 1.) Угол может быть прямым, тупым или острым.
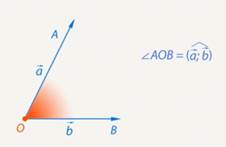
Рис. 1. Угол между векторами
Если векторы сонаправлены, то будем считать, что угол между ними равен 
. (См. Рис. 2.)
Рис. 2. Угол между сонаправленными векторами
Если угол между векторами равен 
, такие векторы называют перпендикулярными. (См. Рис. 3.)
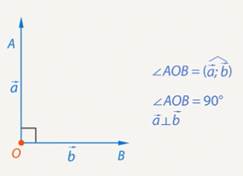
Рис. 3. Перпендикулярные векторы
Если векторы направлены в разные стороны, тогда угол между ними 
. (См. Рис. 4.)
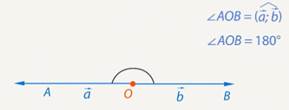
Рис. 4. Угол между противоположно направленными векторами
|
|
|
Скалярное произведение векторов
Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними: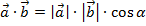 
.
Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно (т. к. 
). (См. Рис. 5.)
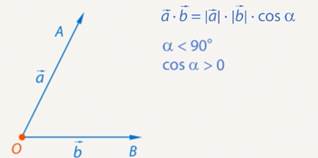
Рис. 5. Случай, когда скалярное произведение положительно
Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно (т. к.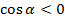 
). (См. Рис. 6.)
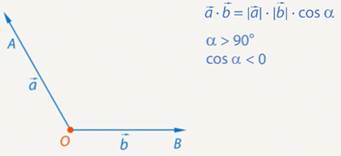
Рис. 6. Случай, когда скалярное произведение отрицательно
Если угол между векторами прямой, то скалярное произведение равно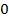 
(т. к. 
). (См. Рис. 7.)
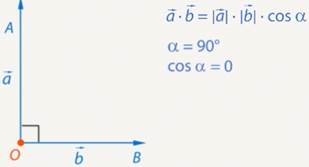
Рис. 7. Случай, когда скалярное произведение равно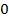
Скалярное произведение через координаты векторов и нахождения косинуса угла между векторами
Важный момент: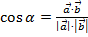 
.
Произведение длин в координатах, мы уже искать умеем – знаменатель сможем преобразовать. А как преобразовать числитель?
Если 
; 
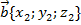, то 
. Формула аналогична плоскостной и доказывается точно так же.
Тогда формула для нахождения косинуса угла между векторами выглядит так:
.
И это очень важный момент. Теперь, если у нас даны две произвольные прямые, каждая задана двумя точками, мы можем найти соответствующие направляющие векторы этих прямых (см. Рис. 8) и посчитать косинус угла между ними по выведенной формуле.
|
|
|
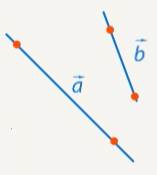
Рис. 8. Угол между произвольными прямыми
Но не стоит забывать, что есть отличие между углом между векторами и углом между прямыми. Угол между прямыми может быть острым или прямым, а угол между векторами может быть еще и тупым. Поэтому соответствующий косинус, который мы найдем у векторов, надо будет взять по модулю, чтобы при необходимости вместо тупого угла найти смежный с ним острый угол.
Свойства скалярного произведения
Остановимся на свойствах скалярного произведения; они абсолютно аналогичны тому, что было в планиметрии.
1. 
(причем 
)
2. 
.
3. ( 
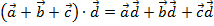
4. 
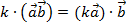, где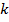 
– число, 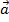, – векторы.
Доказываются эти утверждения аналогично планиметрическим.
Примеры
Задача 1. Найти угол между векторами 
, 
.
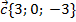Решение. Вспомним, что 
.
По формулам: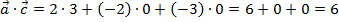 
; 
.
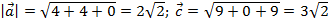Тогда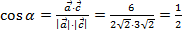 
.
Значит, 
.
Ответ: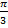 
.
Задача 2. В единичном кубе 
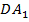найти угол между прямыми 
и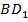 
. (См. Рис. 9.)
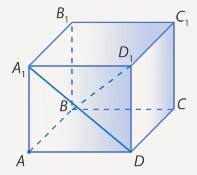
Рис. 9. Иллюстрация к условию
Решение. Сразу отметим, что требуется найти угол между прямыми, то есть угол между ними будет острым. Значит, если косинус получится отрицательным, то надо взять его по модулю, найдя смежный острый угол.
Способ 1. Введем систему координат. (См. Рис. 10.)
|
|
|
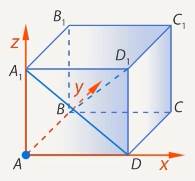
Рис. 10. Ввели систему координат
Найдем координаты интересующих нас точек: 
, 
, 
, 
.
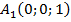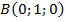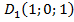Теперь найдем координаты векторов: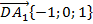 
, 
.
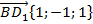Тогда нужно найти косинус угла между данными векторами: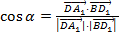 
. Тогда 
.
Значит, 
. Тогда эти векторы перпендикулярны, а тогда и угол между исходными прямыми – прямой, то есть .
Способ 2. Перенесем вектор 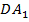параллельно так, чтобы точка 
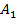совместилась с точкой 
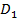, получим вектор 
, тогда найдем угол между 
и 
. (См. Рис. 11.)
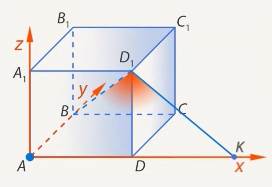
Рис. 11. Иллюстрация ко второму способу решения
Способ 3. Используем теорему о трех перпендикулярах. Проекцией прямой 
на плоскость передней грани является прямая 
, которая перпендикулярна 
(как диагональ квадрата). (См. Рис. 12.) Значит, исходные прямые перпендикулярны.
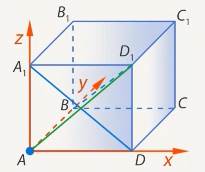
Рис. 12. Прямая 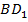и ее проекция
Ответ: .
В правильной треугольной призме 
, все ребра которой равны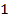 
, найдите косинус угла между прямым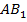и 
и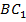 
. (См. Рис. 13.)
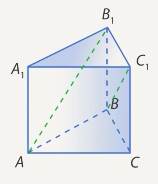
Рис. 13. Иллюстрация к задаче
Решение. 1. Введем систему координат. (См. Рис. 14.)
Рис. 14. Ввели систему координат
Если сделать выносной рисунок основания призмы, получим уже понятный плоскостной рисунок. (См. Рис. 15.) Тогда мы сможем найти координаты всех интересующих нас точек.
|
|
|
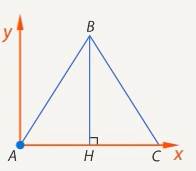
Рис. 15. Выносной рисунок основания призмы
Точка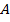 
имеет координаты 
. Точка 
– 
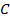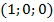. Точка 
– 
.
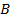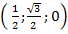Тогда точка 
имеет координаты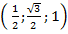 
, а точка 
– 
.
2. Найдем координаты векторов 
и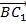 
:
, 
.
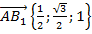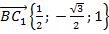3. Найдем длины векторов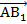 
и :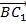
.
.
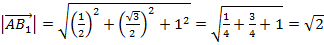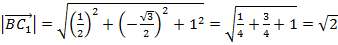4. Найдем скалярное произведение векторов и :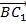
5. Найдем косинус угла между прямым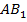и и :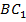
, 
, 
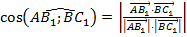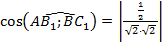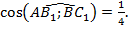
Ответ: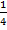 
.
Заключение
На этом занятии мы ввели понятие скалярного произведения для пространства, выяснили, что скалярное произведение обладает теми же свойствами и соответствующими формулами, что и для плоскости. Разобрали формулу скалярного произведения через координаты, поняли, как искать угол между векторами через координаты и между прямыми через координаты, не забыв, что в определенных условиях возникает модуль. То есть если косинус угла между векторами отрицателен, скалярное произведение векторов отрицательно (а мы ищем угол между прямыми), то соответствующий косинус, который тоже будет отрицателен, надо взять по модулю.
Дата добавления: 2020-11-23; просмотров: 65; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!