Построение разверток поверхностей геометрических тел.
Г.
Проецирование геометрических тел. Построение развёртки поверхности геометрического тела .
Проецирование геометрических тел.
Формы деталей, встречающихся в технике, представляют собой сочетание различных геометрических тел или их частей.
Для выполнения и чтения чертежей деталей нужно знать, как изображаются геометрические тела.
Построение проекций прямого цилиндра с вертикальной осью (рис. 1, а) начинают с изображения основания цилиндра, представляющего собой круг. Поскольку круг расположен параллельно плоскости проекций π1 и, следовательно, изображается на ней без искажений, его горизонтальная проекция – круг, а фронтальная и профильная – горизонтальные отрезки прямых, равные диаметру круга. Фронтальная и профильная проекции цилиндра очерчиваются отрезками прямых, представляющими проекции его основания и крайних образующих. На всех проекциях проводят оси симметрии. Размеры цилиндра определяются диаметром его основания и высотой.
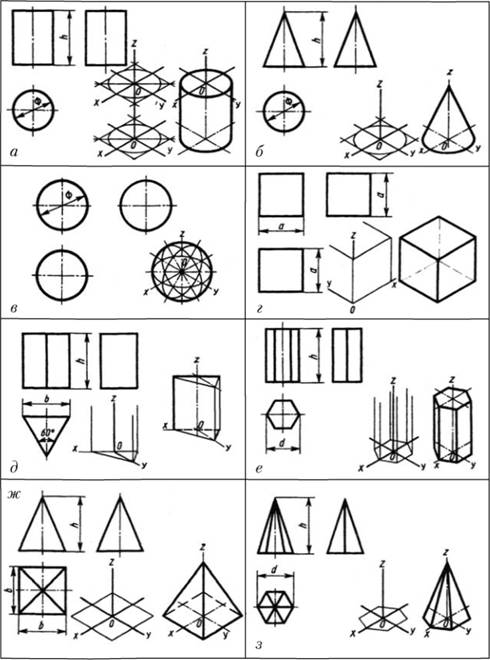
Рисунок 1 - Проекции геометрических тел
Фронтальная и профильные проекции цилиндра одинаковы, поэтому в данном случае профильная проекция лишняя. На рис. 1 чертежи всех геометрических тел выполнены в трех проекциях лишь с той целью, чтобы показать, какие проекции эти тела имеют.
Одно изображение конуса вращения (рис. 1, б) сходно с изображением цилиндра. Так, на горизонтальной проекции конус изображен кругом. На нем наносят центровые линии. Диаметр круга равен диаметру основания конуса. Два других изображения конуса – равнобедренные треугольники. На этих проекциях также наносят оси симметрии. Для конуса указывают диаметр его основания и высоту.
|
|
|
На рис. 1, в представлены чертеж и наглядное изображение шара. Все проекции шара – окружности. Диаметр их равен диаметру шара. На каждом изображении проводят центровые линии.
Так же как и шар, куб имеет три одинаковые проекции (рис. 1, г). Все грани его – квадраты. Размеры куба определяют три измерения: длину, ширину и высоту, равные между собой.
Построение изображений правильной треугольной призмы (рис. 1, д) следует начинать с основания – равностороннего треугольника. На фронтальной плоскости проекций задняя грань призмы изображается в натуральную величину, две передние – с искажением ширины. На профильной проекции ширина прямоугольника равна высоте фигуры основания призмы. На горизонтальной и фронтальной проекциях проводят осевые линии, на профильной проекции ось симметрии отсутствует. Для правильной треугольной призмы указывают ее высоту, длину стороны основания и угол.
Построение прямоугольных проекций правильной шестиугольной призмы (рис. 1, е) также начинают с вычерчивания вида сверху, который представляет собой правильный шестиугольник. На главном виде средняя грань изображается в натуральную величину, а ширина боковых граней искажена. На профильной проекции грани изображаются искаженными по ширине. Размеры правильной шестиугольной призмы определяют ее высотой и шириной, равной удвоенной длине стороны основания.
|
|
|
На рис. 1, ж приведены три проекции и наглядное изображение правильной четырехугольной пирамиды. Основание ее, параллельное горизонтальной плоскости проекций, проецируется на нее в натуральную величину, т.е. изображается квадратом. Боковые ребра, идущие из вершин основания к вершине пирамиды, изображаются диагоналями. Фронтальная и профильная проекции представляют собой равнобедренные треугольники, высота которых равна высоте пирамиды. На всех проекциях должны быть нанесены оси симметрии. Для правильной четырехугольной пирамиды указывают длины двух сторон основания и высоту.
Аналогичны изображения правильной шестиугольной пирамиды (рис. 1, з). Горизонтальной проекцией ее является правильный шестиугольник с диагоналями, изображающими боковые ребра пирамиды. На фронтальной проекции видны три грани, а на профильной – две. На всех проекциях проводят оси симметрии. Размеры правильной шестиугольной пирамиды определяются ее высотой и шириной, равной удвоенной длине стороны основания.
|
|
|
Построение разверток поверхностей геометрических тел.
Для изготовления кожухов машин, ограждений станков, вентиляционных устройств, трубопроводов и других изделий необходимо из листового материала вырезать их развертки.
Разверткой поверхности многогранника называют плоскую фигуру, полученную в результате последовательного совмещения с плоскостью чертежа всех граней многогранника.
Построение разверток поверхности многогранников состоит из определения натуральной величины граней и построения на плоскости в последовательном порядке всех граней. Размеры граней, если они спроецированы не в натуральную величину, находят способами вращения или перемены плоскостей проекций, приведенными в предыдущем параграфе.
Рассмотрим построение разверток некоторых простейших тел.
Развертка поверхности прямой призмы представляет собой плоскую фигуру, составленную из боковых граней – прямоугольников и двух равных между собой многоугольников оснований. Для примера взята правильная шестиугольная призма (рис. 2, а).
|
|
|
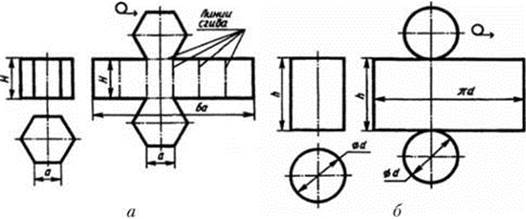
Рисунок 2 - Построение разверток поверхностей призмы и цилиндра
Боковые грани призмы представляют собой равные между собой прямоугольники шириной а и высотой Н, а основания – правильные шестиугольники со стороной, равной а. Так как размеры граней известны, построение развертки нетрудно выполнить. Для этого на горизонтальной прямой последовательно откладывают шесть отрезков, равных стороне основания а шестиугольника, т.е. 6а. Из полученных точек восставляют перпендикуляры длиной, равной высоте призмы Я. Соединяя полученные отрезки, проводят вторую горизонтальную прямую. Полученный прямоугольник (H × 6a) является разверткой боковой поверхности призмы. Затем на одной оси пристраивают фигуру оснований – два шестиугольника со сторонами, равными а. Контур обводят сплошной основной линией, a линии сгиба – штрихпунктирной тонкой с двумя точками.
С помощью подобного построения можно вычертить развертки прямых призм с любой фигурой в основании. Разница будет лишь в количестве и ширине граней боковой поверхности.
Аналогично строится и развертка поверхности цилиндра (рис. 2, б). Только ширина ее равняется πd (длине окружности основания).
Развертка поверхности правильной пирамиды представляет собой плоскую фигуру, составленную из боковых граней – равнобедренных или равносторонних треугольников и правильного многоугольника основания. Для примера взята правильная четырехугольная пирамида (рис. 3, a). Решение задачи осложняется тем, что неизвестна величина боковых граней пирамиды, так как их ребра не параллельны ни одной из плоскостей проекций. Поэтому начинают построение с определения величины ребра SА способом вращения. Определив длину наклонного ребра SA, равную s'a'1, проводят из произвольной точки 5, как из центра, дугу окружности радиусом s'a'1. По этой дуге откладывают четыре отрезка равных стороне основания пирамиды, которое на чертеже спроецировалось в истинную величину. Найденные точки соединяют прямыми с точкой s. Получив таким образом развертку боковой поверхности, пристраивают к основанию одного из треугольников квадрат, равный основанию пирамиды.
Развертка поверхности прямого кругового конуса представляет собой плоскую фигуру, состоящую из кругового сектора и круга (рис. 3, б).
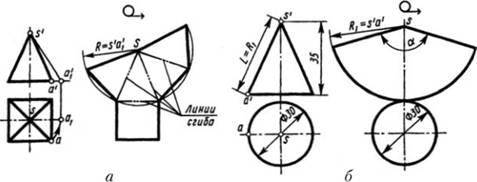
Рисунок 3 - Построение разверток поверхностей пирамиды и конуса
Построение выполняют следующим образом. Проводят осевую линию и из точки, взятой на ней, как из центра, очерчивают радиусом R1, равным образующей конуса s'a'1, дугу окружности. Затем подсчитывают угол сектора по формуле α = 360° • R/L, где R – радиус окружности основания конуса; L – длина образующей боковой поверхности конуса. В примере α = 360° • 15/38 ≈ 142,2°.
Этот угол строят симметрично относительно осевой линии с вершиной в точке S. К полученному сектору пристраивают круг с центром на осевой линии и диаметром, равным диаметру основания конуса.
Домашнее задание.
1. Кратко законспектировать материал на тему: «Проецирование геометрических тел. Построение развёртки поверхности геометрического тела».
2. Выучить материал из учебника Хаскин ,А.М. Черчение: учебник для техникумов/ А.М. Хаскин; Под ред. А.В. Блиока. - 3-е изд., перераб. и доп. - К. : Вища школа, 1979. - с.127-150.
3. Ответить на следующие вопросы:
3.1. Как построить развёртку треугольной прямоугольной призмы?
3.2. Каков алгоритм построения проекций конуса? Цилиндра?
3.3. Как построить развёртку конуса?
Дата добавления: 2020-11-23; просмотров: 533; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
