Наибольшее и наименьшее значение функции.
Рассмотрим случай, когда функция y=f(x) непрерывна на интервале [a;b]. Как известно, такая функция достигает своего наибольшего и наименьшего значения, которые называют также абсолютными экстремумами функции на этом интервале и обозначают соответственно
; 
.
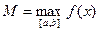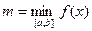Пусть функция y=f(x) непрерывна на интервале [a;b], дифференцируема во всех точках этого интервала и имеет на нем конечное число критических точек первого рода. Нужно найти ее наибольшее и наименьшее значение на интервале [a;b].
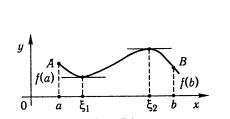
Рис.10.
Понятно, что для точки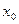 
, где функция достигает своего наибольшего или наименьшего значения могут быть такие случаи:
- если функция монотонна на отрезке [a;b], то своего наименьшего или наибольшего значения она достигает на концах отрезка:
а) если функция возрастающая, то f(a)- ее наименьшее значение, а f(b) - наибольшее ;
б) если функция убывающая, то f(a)- ее наибольшее значение, а f(b) - наименьшее;
- если функция не является монотонной, то своего наибольшего значения она достигает или в одной из точек максимума, или на одном из концов отрезка, а своего наименьшего значения достигает или в одной из точек минимума, или на одном из концов отрезка.
Непрерывная на интервале функция может и не иметь абсолютных е
экстремумов.
Нахождение наибольшего и наименьшего значения функции на заданном интервале.
Чтобы найти наибольшее и наименьшее значение функции на заданном интервале нужно:
|
|
|
1) Найти критические точки функции y=f(x) на интервале [a;b];
2) Вычислить значения функции во всех критических точках, которые принадлежат данному интервалу, и на концах данного интервала;
3) Из полученных значений выбрать наибольшее и наименьшее.
Нахождение наибольшего и наименьшего значений функции широко используется при решении многих практических задач. При этом часто используется свойство функции:
Если функция непрерывна на некотором (открытом или закрытом) интервале и имеет на нем единственный экстремум, то он является ее наименьшим значением в случае минимума и наибольшим – в случае максимума.
3. Решение задач оптимизации.
Задачи на нахождение наибольшего и наименьшего значений функции называют задачами на минимум и максимум, или задачами оптимизации. Обратим внимание, что практический интерес имеют не сами минимумы и максимумы, а значения аргумента, при которых они достигаются.
Рассмотрим одну из задач оптимизации.
Задача.
Из круглого бревна диаметром 6 см. нужно изготовить балку прямоугольного сечения так, чтобы площадь сечения была максимальной.
Решение:
Обозначим через х (см.) одну из сторон прямоугольника в сечении круглого бревна, а другую сторону прямоугольника найдем по теореме Пифагора:
|
|
|
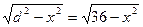
Площадь прямоугольного сечения найдем по формуле:
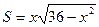
Исследуем функцию S(x) на наибольшее значение на интервале ( 0; 6 ) с помощью производной:
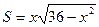
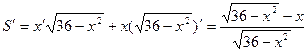
Приравниваем значение производной к нулю и найдем критические точки функции: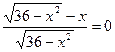 
36 - х² - х² =0
36 = 2х²
18 = х²
х = - 4,2 значение не принадлежит интервалу (0; 6 )
х = 4,2
f´(3) = 5- 9/5 =3,2 ; f´ (5) = - 5,3
Значит при х = 4,2 функция достигает наибольшего значения, то есть одна из сторон прямоугольного сечения бревна имеет значение х = 4,2 (см). Найдем другую сторону прямоугольника
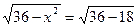= 4,2(см).
Ответ: площадь сечения будет наибольшей, если оно будет иметь размеры:
4,2 Х 4,2 (см).
Задания для закрепления и самоконтроля:
1) Найти наименьшее и наибольшее значение функции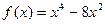 
на отрезке [-1;3] .
Ответ: 
; 
.
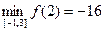2) Найти наибольшее и наименьшее значение функции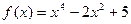 
на интервале [-2;3] .
Ответ: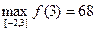 
.
Контрольные вопросы.
1. Какие функции называются монотонными?
2. Какие функции называются возрастающими?
3. Какие функции называются убывающими?
4. Как называются точки, в которых функция имеет производную равную нулю?
5. Как определить наибольшее и наименьшее значение функции на заданном интервале?
|
|
|
6. Где находятся наибольшие и наименьшие значения монотонной на заданном интервале функции?
7. Если функция на интервале имеет единственный экстремум, то как определить наибольшее и наименьшее значение функции на данном интервале?
Литература:
В.П.Дубовик, И.И.Юрик «Высшая математика», К., 2003, ст.246-248, ст.253-260.
Дата добавления: 2020-11-23; просмотров: 59; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!