Дифференциальные уравнения движения Эйлера и Навье-Стокса

Основы гидродинамики

При истечении жидкости движущей силой является разность давлений, которая создается с помощью насосов или компрессоров, а также вследствие разности уровней жидкости (по принципу самотека).

Для гидромеханических процессов можно выделить три задачи:

1. Внутренняя задача гидродинамики .

Которая описывает движение жидкостей и газов внутри труб и каналов.

2. Внешняя задача гидродинамики .

Которая описывает движение частиц в газообразной или жидкой средах (обтекание жидкостями различных тел).

3. Смешанная задача гидродинамики .

Которая описывает движение жидкостей или газов через пористый слой.

Все явления связанные с движением жидкости или газа, обычно описывается системой дифференциальных уравнений, включающих уравнения движения (Навье-Стокса) и уравнение неразрывности (сплошности) потока.

Уравнение неразрывности потока

Рассмотрим поток, для которого соблюдается условие сплошности (неразрывности) движения, т.е. не образуются пустоты, незаполненные жидкостью.

Выделим внутри потока неустановившегося движения сжимаемой жидкости элементарный параллелепипед объемом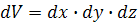

Обозначим составляющую скорости потока вдоль оси в точках на левой грани параллелепипеда

Тогда:

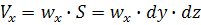
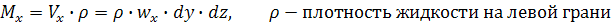
За промежуток времени :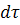

Приход: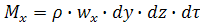

На правой грани плотность и скорость могут отличаться:

· Скорость ;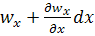

· Плотность .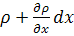

Тогда через правую грань параллелепипеда за время 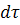вытечет жидкости:

Расход:

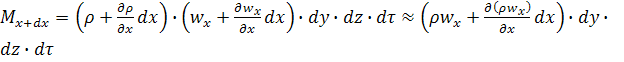
(величинами малых порядков пренебрегаем)

Считается, что

Приращение массы жидкости в параллелепипеде вдоль оси х:

По аналогии будет для осей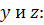

Где

Общее накопление массы в параллелепипеде за время 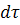равно сумме ее приращений вдоль всех осей координат:

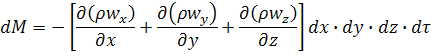
Изменение массы в полностью заполненном жидкостью объеме параллелепипеда при его неизменных размерах возможно только вследствие изменения плотности жидкости в этом же объеме во времени:

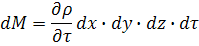
Приравнивая и сокращая на 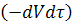, получаем:

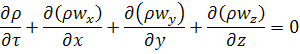
Это дифференциальное уравнение неразрывности потока для неустановившегося движения сжимаемой жидкости.

Для установившегося потока плотность не меняется во времени 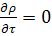, т.е. массы втекающей и вытекающей жидкости равны, и изменения массы в параллелепипеде не происходит:

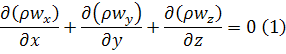
Для установившегося движения несжимаемой жидкости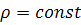

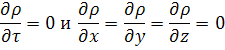
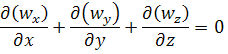
Это дифференциальное уравнение неразрывности потока несжимаемой жидкости.

В интегральной форме (проинтегрировав уравнение 1) для одномерного потока вдоль оси 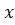, проходящего через сечение :

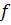При

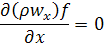
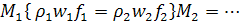
Это уравнение постоянства расхода для установившегося движения.

При установившемся движении жидкости, полностью заполняющей трубопровод, через каждое его поперечное сечение проходит в единицу времени одно и то же количество жидкости.

Для несжимаемой жидкости:

Уравнение расхода

Расход жидкости – количество ее, протекающее через поперечное сечение потока в единицу времени:

- объемный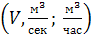

- массовый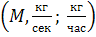

Расход 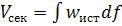; где 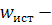истинная скорость

Поскольку скорость потока изменяется по сечению трубы (и в ряде случаев закон распределения скоростей неизвестен), для упрощения в расчетах используют понятие «средняя» скорость: .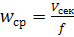

Тогда уравнение объемного расхода

Массовый расход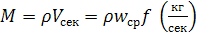

Величина представляет собой массовую скорость: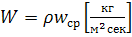

Скорости капельных жидкостей в различных поперечных сечениях трубопровода обратно пропорциональны площадям этих сечений.

Уравнение постоянства расхода является частным случаем закона сохранения массы и выражает материальный баланс потока.

При кипении уравнение неразрывности нарушается.

Дифференциальные уравнения движения Эйлера и Навье-Стокса

Баланс действующих в потоке сил выражается в случае движения идеальной жидкости уравнениями Эйлера, в случае движения реальной (вязкой) жидкости – уравнениями Навье-Стокса.

Рассмотрим общий случай – неустановившегося движения вязкой несжимаемой 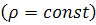жидкости.

Выделим в потоке элементарный параллелепипед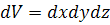

На этот элемент жидкости действует следующие силы:

1. Сила тяжести.

2. Поверхностные силы:

а) Нормальные силы 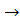давление

б) Касательные силы трение

При равновесии касательные силы равны нулю

Рассмотрим проекции сил тяжести и давления.

На ось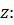

Сила тяжести:

Сила давления:

- На нижнюю грань:

- На верхнюю грань:

Сумма равна:

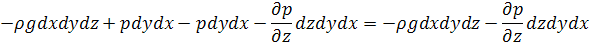
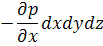
На ось

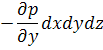
Для учета сил вязкости рассмотрим одномерное движение в направлении оси

Действие сил трения проявляется в возникновении касательных напряжений 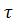(силе трения на единицу поверхности) на поверхности верхней и нижней граней.

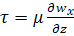уравнение Ньютона

Направление касательных сил ( ):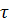

Более быстрые вышележащие слои «разгоняют» параллелепипед, а более медленные нижележащие слои «затормаживают» его.

Проекция равнодействующих сил трения на ось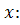

Подставим значение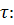

Для трехмерного потока составляющая скорости будет меняться по всем трем осям координат:

Проекция на ось

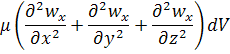
Сумма частных вторых производных по осям координат – оператор Лапласа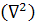

Следовательно:

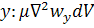
на ось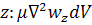

В соответствии с основным принципом динамики сумма проекций сил на оси координат равна произведению массы жидкости на проекции ускорения на оси координат:

масса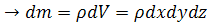

ускорение для неустановившегося потока полная (субстанциональная) производная скорости по времени:

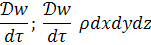
Сокращая на :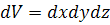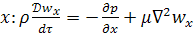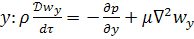

на ось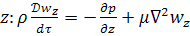

⁼ .

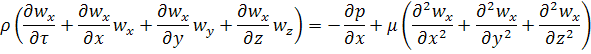
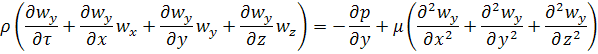
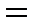
Это уравнение Навье-Стокса, описывающее движение вязкой несжимаемой жидкости.

Оно описывает баланс сил тяжести, вязкости и гидростатического давления в неустановившемся потоке несжимаемой жидкости.

Уравнения Навье-Стокса совместно с уравнением неразрывности дают возможность решить основную задачу гидродинамики – определить поля скоростей, давления и плотности в жидкости, движущейся под действием заданных сил.

Однако уравнение Навье-Стокса в большинстве случаев не может быть решено в общем виде. Решение получено только для некоторых простейших случаев движения жидкости.

Преобразование уравнения Навье-Стокса возможно методами теории подобия.

Для идеальной жидкости вязкость отсутствует и уравнение Навье-Стокса преобразуется в дифференциальное уравнение движения Эйлера.

Для неустановившегося движения:

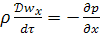
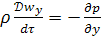
Раскрывая производные:

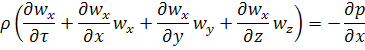
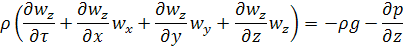
Это дифференциальное уравнение Эйлера для неустановившегося движения идеальной жидкости.

Для установившегося потока локальные изменения скорости равны нулю:

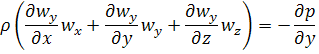
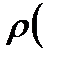
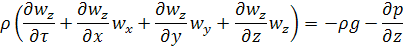
Ошибка была в уравнении 3!!!

Это дифференциальные уравнения Эйлера для установившегося потока.

Эти диф. уравнения являются основой для расчета процессов (интегрированием или чаще при помощи теории подобия).

Дата добавления: 2020-11-15; просмотров: 326; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!