О расширении множества натуральных чисел

Большинство применений математики связано с измерением вели­чин. Однако для этих целей натуральных чисел недостаточно: не всег­да единица величины укладывается целое число раз в измеряемой величине. Чтобы в такой ситуации точно выразить результат измере­ния, необходимо расширить запас чисел, введя числа, отличные от натуральных. К этому выводу люди пришли еще в глубокой древно­сти: измерение длин, площадей, масс и других величин привело снача­ла к возникновению дробных чисел - получили рациональные числа, а в V в до н.э. математиками школы Пифагора было установлено, что существуют отрезки, длину которых при выбранной единице длины нельзя выразить рациональным числом. Позднее, в связи с решением этой проблемы, появились числа ирра­циональные. Рациональные и иррацио­нальные числа назвали действительными. Строгое определение действительного числа и обоснование его свойств было дано в XIX в.

 

Взаимосвязи между различными множествами чисел (N, Z, Q и R) можно изобразить наглядно при помощи кругов Эйлера (рис 26).

 

Действительные числа – не последние в ряду различных чисел. Процесс, начавшийся с расширения множества натуральных чисел, продолжается и сегодня ­– этого требует развитие различных наук и самой математики.

 

Знакомство учащихся с дробными числами происходит, как правило, в начальных классах. Затем понятие дроби уточняется и расширяется в средней школе. В связи с этим учителю необходимо владеть понятием дроби и рационального числа, знать правила выполнения действий над рациональными числами, свойства этих действий. Все это нужно не только для того, чтобы математически грамотно ввести понятие дроби и обучать младших школьников выполнять с ними действия, но и, что не менее важно, видеть взаимосвязи множеств рациональных и действительных чисел с множеством натуральных чисел. Без их понимания нельзя решить проблему преемственности в обучении математике в начальных и последующих классах школы.

 

Расширение множества N натуральных чисел будет происходить в такой последовательности: сначала строится множество 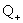положительных рациональных чисел, затем показывается, как его можно расширить до множества 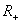положительных действительных чисел, и, наконец, описывается расширение множества 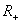до множества R всех действительных чисел.

Действительные числа

Одним из источников появления десятичных дробей является деление натуральных чисел, другим – измерение величин. Выясним, например, как могут получиться десятичные дроби при измерении длины отрезка.

 

Пусть x – отрезок, длину которого надо измерить, e – единичный отрезок (рис.29). Длину отрезка x обозначим буквой X, а длину отрезка e – буквой E.

 

 

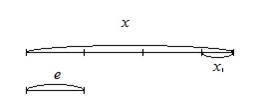
Пусть отрезок x состоит из n отрезков равных e, и отрезка 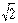, который короче отрезка e (рис.) т.е. . Числа n и n+1 есть приближенные значения длины отрезка x при единице длины E с недостатком и с избытком с точностью до 1.

 

Чтобы получить ответ с большей точностью, возьмем отрезок 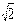– десятую часть отрезка e и будем укладывать его в отрезке 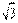. При этом возможный два случая.

 

1) Отрезок 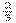уложился в отрезке 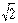точно n раз. Тогда длина n отрезка x выражается конечной десятичной дробью: 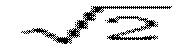. Например, .

 

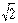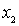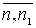2) Отрезок оказывается состоящим из n отрезков, равных , и отрезка , который короче отрезка . Тогда , где и 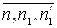- приближенные значения длины отрезка x с недостатком и с избытком с точностью до 0,1.

 

Ясно, что во втором случае процесс измерения длины отрезка x можно продолжать, взяв новый единичный отрезок 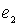- сотую часть e.

 

На практике этот процесс измерения длины отрезка на каком-то этапе закончится. И тогда результат измерения длины отрезка будет либо натуральное число, либо конечная десятичная дробь. Если же представить этот процесс измерения длины отрезка в идеале (как и делают в математике), то возможны два исхода:

 

1) На k-том шагу процесс измерения окончится. Тогда длина отрезка x выразится конечной десятичной дробью вида .

 

2) Описанный процесс измерения длины отрезка x продолжается бесконечно. Тогда отчет о нем можно представить символом , который называют бесконечной десятичной дробью.

 

Как убедиться в возможности второго исхода? Для этого достаточно произвести измерение длины такого отрезка, для которого известно, что его длина выражена, например, рациональным числом 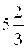. Если бы оказалось, что в результате измерения длины такого отрезка получается конечная десятичная дробь, то это означало бы, что число 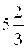можно представить в виде конечной десятичной дроби, что невозможно: .

 

Итак, при измерении длин отрезков могут получиться бесконечные десятичные дроби. Но всегда ли эти дроби периодические? Ответ на этот вопрос отрицателен: существуют отрезки, длины которых нельзя выразить бесконечной периодической дробью (т.е. положительным рациональным числом) при выбранной единице длины. Это было важнейшим открытием в математике, из которого следовало, что рациональных чисел недостаточно для измерения отрезков.

 

Теорема. Если единицей длины является длина стороны квадрата, то длина диагонали этого квадрата не может быть выражена положительным рациональным числом.

 

Доказательство. Пусть длина стороны квадрата выражается числом 1. Предположим противное тому, что надо доказать, т.е., что длина диагонали AC квадрата ABCD выражается несократимой дробью . Тогда по теореме Пифагора, выполнялось бы равенство . Из него следует, что . Значит, 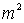- четное число, тогда и число m – четно (квадрат нечетного числа не может быть четным). Итак, . Заменив в равенстве число m на 2p, получаем, что 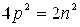, т.е. 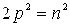. Отсюда следует, что четно, следовательно, n – четное число. Таким образом, числа m и n четны, значит, дробь можно сократить на 2, что противоречит предположению о ее несократимости. Установленное противоречие доказывает, что если единицей длины является длина стороны квадрата, то длину диагонали этого квадрата нельзя выразить рациональным числом.

 

Из доказанной теоремы следует, что существуют отрезки, длины которых нельзя выразить положительным числом (при выбранной единице длины), или, другими словами, записать в виде бесконечной периодической дроби. И значит, получаемые при измерении длин отрезков бесконечные десятичные дроби могут быть не периодическими.

 

Считают, что бесконечные непериодические десятичные дроби являются записью новых чисел – положительных иррациональных чисел. Так как часто понятия числа и его записи отождествляют, то говорят, что бесконечные непериодические десятичные дроби – это и есть положительные иррациональные числа.

 

Мы пришли к понятию положительного иррационального числа через процесс измерения длин отрезков. Но иррациональные числа можно получить и при извлечение корней из некоторых рациональных чисел. Так, 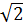, , 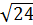- это иррациональные числа. Иррациональными являются также lg 5, sin 31, числа π=3,14…, e=2,7828… и другие.

 

Множество положительных иррациональных чисел обозначают символом J+.

 

Объединение двух множеств чисел: положительных рациональных и положительных иррациональных называют множеством положительных действительных чисел и обозначают R+. Таким образом, Q+ 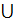J+ = R+.

 

Любое положительное действительное число может быть представлено бесконечной десятичной дробью – периодической (если оно является рациональным), либо непериодической (если оно является иррациональным).

 

Действия над положительными действительными числами сводится к действиям над положительными рациональными числами.

 

Для этого надо ввести понятие приближенного значения действительного числа по недостатку и по избытку.

 

Пусть a=n, n1 n2… nk… - некоторое действительное число. Приближенным значением числа a по недостатку с точностью до 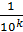называется число ak=n, n1 n2… nk (т.е. приближенное значение числа a по недостатку получается, если взять целую часть и первые k цифр после запятой, а все остальные цифры отбросить).

 

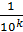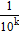Приближенным значением числа a=n, n1 n2… nk… по избытку с точностью до называется число =n, n1 n2… nk+ (т.е. приближенное значение числа a по избытку получается, если в записи n, n1 n2… nk последнюю цифру увеличить на 1).

 

Для любого действительного числа a справедливо неравенство ak a< .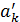

 

Например, десятичным приближением числа =1,73205… по недостатку с точностью до 0,001 является число 1,732, а по избытку – число 1,733.

 

Видим, что десятичные приближения действительного числа являются конечными десятичными дробями. На этом и основываются, определяя действия над положительными действительными числами.

 

Пусть даны действительные числа a и b, ak и bk – их приближенные значения по недостатку, 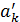и - приближенные значения по избытку.

 

Суммой положительных действительных чисел a и b называется такое число a+b, которое удовлетворяет следующему неравенству:

 

ak +bk 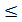a+b < + .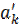

 

Найдем, например, сумму 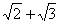с точностью до 0,001. Возьмем десятичные приближения данных чисел с точностью до 0,001:

 

,

 

.

 

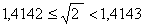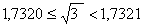Тогда , а с точностью до 0,001.

 

Произведением положительных действительных чисел a и b называется число , которое удовлетворяет следующим условиям:

 

.

 

Найдем, например, произведение 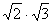с точностью до 0,1. Возьмем десятичные приближения данных чисел с точностью до 0,01:

 

,

 

.

 

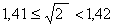Тогда , а 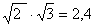с точностью до 0,01.

 

Для любых положительных действительных чисел выполняются следующие равенства:

 

1) ;

 

2) ;

 

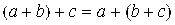3) ;

 

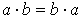4) ;

 

5) .

 

Вычитание положительных действительных чисел определяется как действие, обратное сложению. Для нахождения значения разности по недостатку и по избытку пользуются известными зависимостями между компонентами действий:

 

.

 

Деление положительных действительных чисел определяется как действие, обратное умножению.

Понятие дроби

Пусть требуется измерить длину отрезка x с помощью единичного отрезка e (рис.27). При измерении оказалось, что отрезок x состоит из трех отрезков, равных e, и отрезка, который короче отрезка e. В этом случае длина отрезка x не может быть выражена натуральным числом.

 

 

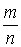
Однако если отрезок e разбить на 4 равные части, то отрезок x окажется состоящим из 14 отрезков, равных четвертой части отрезка e. И тогда, говоря о длине отрезка x, мы должны указать два числа 4 и 14: четвертая часть отрезка e укладывается в отрезке точно 14 раз. Поэтому условились длину отрезка x записывать в виде , где E – длина единичного отрезка e, а символ называть дробью.

 

В общем виде понятие дроби определяют так.

 

Пусть даны отрезок x и единичный отрезок e, длина которого E. Если отрезок x
состоит из m отрезков, равных n-ой части отрезка e, то длина отрезка x может быть представлена в виде , где символ называют дробью (и читают “эм энных”).

 

В записи дроби числа m и n – натуральные, m называется числителем, n – знаменателем дроби.

 

Дробь называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателя или равен ему.

 

Ранее показано, что четвертая часть отрезка e уложилась в отрезке x точно 14 раз. Очевидно, это не единственный вариант выбора такой части отрезка e, которая укладывается в отрезок x целое число раз. Можно взять восьмую часть отрезкаe, тогда отрезок x будет состоять из 28 таких частей и его длина будет выражаться дробью . Можно взять шестнадцатую часть отрезка
e, тогда отрезок x будет состоять из 56 таких частей и его длина будет выражаться дробью .

 

Вообще длина одного и того же отрезка x при заданном единичном отрезке e может выражаться различными дробями, причем, если длина выражена дробью , то она может быть выражена и любой дробью вида , где k
– натуральное число.

 

Теорема. Для того чтобы дроби и выражали длину одного и того же отрезка, необходимо и достаточно, чтобы выполнялось равенство .

 

Доказательство этой теоремы мы опускаем.

 

Две дроби и называются равными, если .

 

Если дроби равны, то пишут .

 

Например, , так как , а , потому что , а и .

 

Из сформулированных выше теоремы и определения следует, что две дроби равны тогда и только тогда, когда они выражают длину одного и того же отрезка.

 

Нам известно, что отношение равенства дробей рефлексивно, симметрично и транзитивно, т.е. является отношением эквивалентности.

 

Из определения равных дробей вытекает основное свойство дроби. Напомним его.

 

Если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится дробь, равная данной.

 

На этом свойстве основано сокращение дробей и приведение дробей к общему знаменателю.

 

Сокращение дробей – это замена данной дроби другой, равной данной, но с меньшим числителем и знаменателем.

 

Если числитель и знаменатель дроби одновременно делятся только на единицу, то дробь называют несократимой. Например, – несократимая дробь, так как её числитель и знаменатель делятся одновременно только на единицу, т.е D(5, 17) = 1.

 

Приведение дробей к общему знаменателю – это замена данных дробей равными им дробями, имеющими одинаковые знаменатели. Общим знаменателем двух дробей и является общее кратное чисел и , а наименьшим общим знаменателем – их наименьшее кратное K(n, q).

 

Приведем к наименьшему общему знаменателю дроби и .

 

Решение. Разложим числа 15 и 35 на простые множители: , . Тогда . Поскольку , то , .

 

---

Дата добавления: 2020-11-15; просмотров: 367; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!