Выполнение контрольной работы
Конспект урока математики
Дата
| 95 | 96 | 97 | 98 |
| 26.10.20 |
Группа № 95 мастер по ремонту и обслуживанию автомобилей 1 курс
Группа №96 профессия повар, кондитер курс1
Группа №97 профессия машинист крана(крановщик) 1 курс
Группа №98 профессия тракторист-машинист сельскохозяйственного производства
Курс
Тема: « Контрольная работа №2 «Степенная функция »
Урок №25
Форма работы: индивидуальная, дистанционное обучение.
Тип урока: урок контроля и учета знаний, умений и навыков
Цель урока: закрепление теоретического материала; совершенствование навыков решения задач по теме» Степенная функция
Используемая литература: Математика : алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа.
10-11 классы: учеб.для общеобразоват.организаций: базовый и углубл.уровени./Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.- 5 изд.- М.: Просвещение , 2018г
Интернет- ресурсы : Математика в Открытом колледже: http://www.mathematics.ru
Ход занятия
1. Организационный этап.
Мотивационный модуль. Ребята, для успешного выполнения контрольной работы, необходимо повторить теоретический материал по теме « Степенная функция»
|
|
|
Определение. Функция вида у=хn, где n- любое действительное число, называют степенной функцией.
При n=2, y=x2 — парабола.
При n=3, y=x3 — кубическая парабола.
График степенной функции y=xn, где n — чётное число (4,6,8...), принимает вид параболы.
Рисунок 2 – график функции y=xn, где n — чётное число
График степенной функции y=xn, где n — нечётное число (5,7,9...), принимает вид кубической параболы.
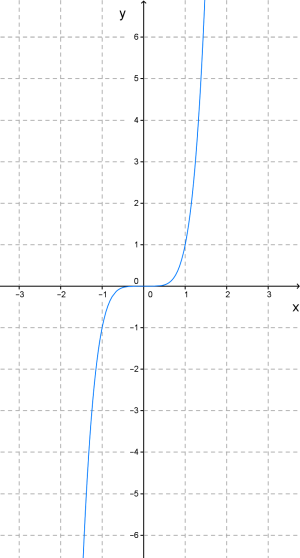
Рисунок 3 – график функции y=xn, где n — нечётное число
Если показатель степени — целое отрицательное число, то степенная функция задаётся формулой y=x−n или y=1/xn.
График степенной функции y=x−n, в случае, когда n — чётное число (4,6,8...), принимает вид:
Рисунок 4 – график функции y=x−n, при n — чётное число
Например, такой вид принимают графики функций y=x−4,y=x−8.
График степенной функции y=x−n, в случае, когда n — нечётное число (5,7,9...), принимает вид гиперболы:
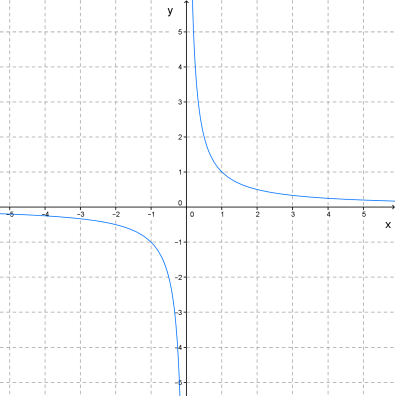
Рисунок 5 – график функции y=x−n, при n — нечётное число
Например, такой вид принимают графики функций y=x−5,y=x−11.
Функции такого вида называются дробно-линейными.
Рассмотрим графики степенных функций y=xm/n с положительным дробным показателем m/n.
|
|
|
1. Степенная функция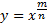 
, где 
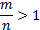> неправильная дробь (числитель больше знаменателя).
График — ветвь параболы:
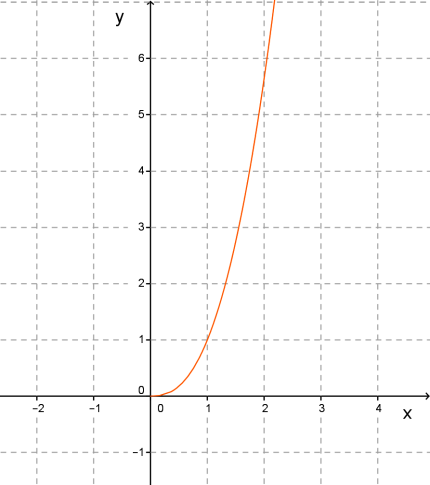
Рисунок 6 – 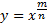, где
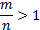
Свойства функции 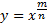, где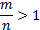
1.D(f)=[0;+∞);
2.E(f)=[0;+∞);
3. не является ни чётной, ни нечётной;
4. возрастает при x∈[0;+∞);
5. не имеет наибольшего значения, yнаим=0;
6. не ограничена сверху, ограничена снизу;
7. выпукла вниз;
8. непрерывна.
2. Степенная функция 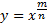, где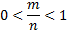 
— правильная дробь (числитель меньше знаменателя).
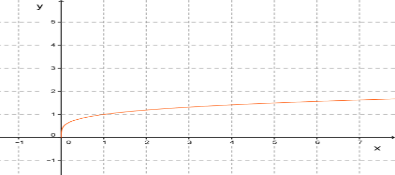
Рисунок 7 - функция 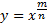, где
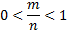
Свойства функции 
, где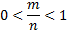
1.D(f)=[0;+∞);
2.E(f)=[0;+∞);
3. не является ни чётной, ни нечётной;
4. возрастает при x∈[0;+∞);
5. не имеет наибольшего значения, yнаим=0;
6. не ограничена сверху, ограничена снизу;
7. выпукла вверх;
8. непрерывна.
Рассмотрим степенные функции с отрицательным дробным показателем степени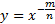 
График — ветвь гиперболы.
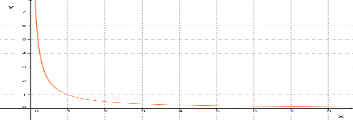
Рисунок 8 - функция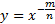
График имеет горизонтальную асимптоту у=0 и вертикальную асимптоту х=0.
Свойства функции .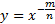
1.D(f)=(0;+∞);
2.E(f)=(0;+∞);
3. не является ни чётной, ни нечётной;
4. убывает при x∈(0;+∞);
5. не имеет ни наибольшего, ни наименьшего значения;
6. не ограничена сверху, ограничена снизу;
|
|
|
7. выпукла вниз;
8. непрерывна.
Итак, на основании всего вышеперечисленного, можно сделать вывод в виде таблицы:
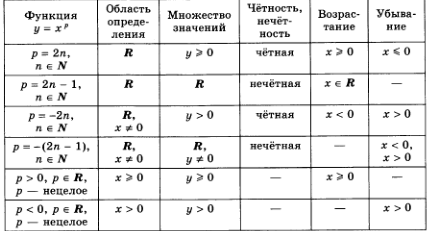
Выполнение контрольной работы
Контрольная работа № 2
Тема «Степенная функция»
Вариант – 1
1. Найти область определения функции
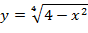
2. Изобразить эскиз графика функции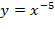 
1) Выяснить, на каких промежутках функция убывает.
2) Сравнить числа:
А)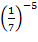 
и 1; б) 
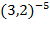и 
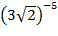
3. Решить уравнение:
1) 
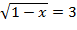2) 
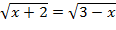3) 
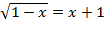
4) 
4. Найти функцию, обратную к функции
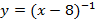
указать её область определения и множество занчений.
5. Решить неравенство 
Контрольная работа № 2
Тема «Степенная функция»
Вариант – 2
1. Найти область определения функции
2. Изобразить эскиз графика функции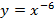 
1) Выяснить, на каких промежутках функция возрастает.
2) Сравнить числа: а)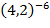 
и 1; б) 
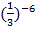и 
3. Решить уравнение:
1) 
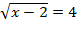2) 
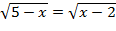3) 
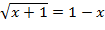
4) 
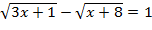
4. Найти функцию, обратную к функции
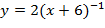
указать её область определения и множество занчений.
5. Решить неравенство 
Выполненную работу отправить личным сообщение в ВК
Дата добавления: 2020-11-15; просмотров: 84; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!