Раздел 3. Основы математического анализа
Тема 3.1. Функции одной действительной переменной. Предел функции.
План.
1) Понятие функции одной действительной переменной. Понятие предела функции в точке.
2) Вычисление пределов.
3) Приращение функции. Непрерывность функции.
1.
Переменная 
называется функцией переменной 
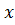, если каждому допустимому 
соответствует единственное значение .
Число А называется пределом функции 
в точке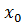 
, если для любого числа 
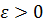существует число 
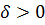такое, что для всех , удовлетворяющих условию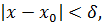 
выполняется неравенство
.
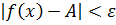Обозначение:
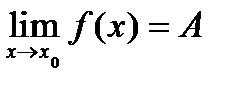
Теоремы о пределах.
1) 
2) 
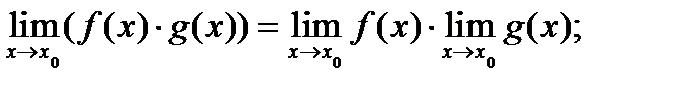
3) 
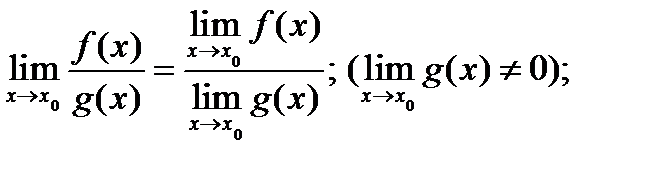
4) 
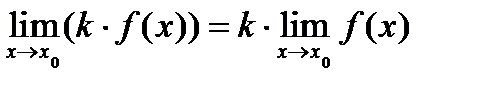
2.
Равенства на память
Неопределенности
Методы вычисления пределов
1) Вместо подставить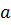 
.
2) При неопределенности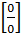 
сократить функцию.
3) При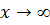 
разделить числитель и знаменатель на высшую степень переменной.
4) Если переменная под знаком корня, то умножить на сопряженное выражение.
Пример. Вычислить пределы: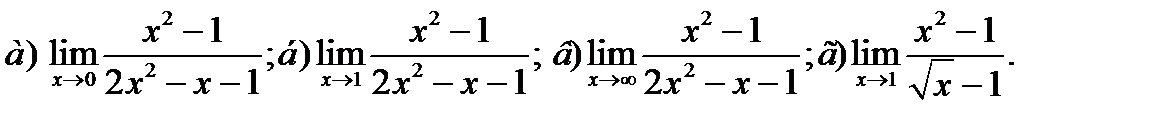 
Решение.
3.
- первоначальное значение аргумента.
- новое значение аргумента.
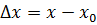– приращение аргумента.
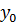- первоначальное значение функции.
- новое значение функции.
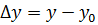– приращение функции.
Функция называется непрерывной в точке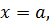 
если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, то есть 
.
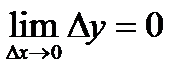Точка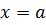 
называется точкой непрерывности. В противном случае она называется точкой разрыва.
|
|
|
Функция называется непрерывной на промежутке, если она непрерывна в каждой точке этого промежутка.
Пример.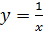 
имеет точку разрыва 
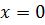, непрерывна на промежутке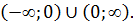 
Тема 3.2. Производная функции.
План
1) Понятие производной. Ее физический и геометрический смысл.
2) Формулы дифференцирования.
3) Производная сложной функции.
1.
- определение производной функции в точке.
Операция нахождения производной называется дифференцированием.
Физический смысл производной состоит в том, что мгновенная скорость материальной точки при прямолинейном неравномерном движении равна производной от пути по времени.
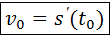
Геометрический смысл производной состоит в том, что ее значение в точке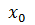 
равно угловому коэффициенту касательной, проведенной к графику данной функции в данной точке.
| y |
|
|
|
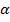
| x |
| 0 |
2.
Формулы дифференцирования:
( u ± v ) ¢ = u ¢ ± v ¢ ;
(uv) ¢ =u ¢ v + v ¢ u;
(cu) ¢ =cu ¢ ;
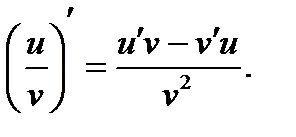
Таблица производных основных элементарных функций:
1) 
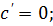
2) 
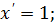
3) 
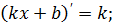
4) 
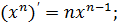
5) 
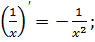
6) 
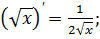
7) 
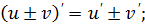
8) 
9) 
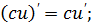
10) 
;
11) 
12) 
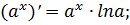
13) 
14) 
;
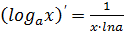15) 
;
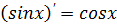16) 
17) 
18) 
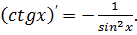
Пример. Найти производные функций:
|
|
|
Решение.
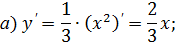
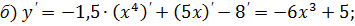
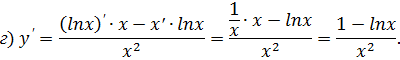
3.
Функция называется сложной, если ее аргументом является функция.
Пример. Назвать функции:
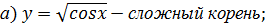
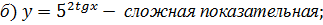
Производная сложной функции равна произведению производных всех функций в нее входящих.
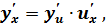
где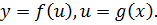 
Пример. Найти производные функций:
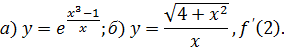
Решение.
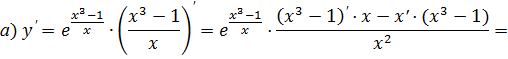
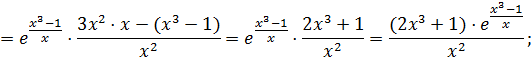
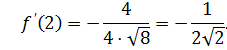
Тема 3.3.Неопределенный интеграл
План.
1) Понятие первообразной и неопределенного интеграла. Свойства неопределенного интеграла.
2) Методы интегрирования неопределенного интеграла.
1.
Первообразной для функции f ( x ) называется функция F ( x ), для которой при любом допустимом значении х справедливо равенство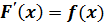 
Пример. Найти три первообразных для функции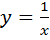 
.
Решение.
Действительно,
.
Неопределенным интегралом 
называется совокупность всех первообразных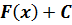 
.
Пример.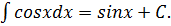 
Дата добавления: 2020-11-15; просмотров: 51; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!