Силы инерции при ускоренном поступательном движении системы отсчета

⇐ ПредыдущаяСтр 2 из 2

Рассмотрим шарик, подвешенный на нити, точка подвеса которого 0' движется с ускорением 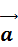относительно некоторой инерциальной системы отсчета К. Нить подвеса отклоняется от вертикали на некоторый угол .

Угол этот таков, чтобы равнодействующая 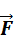силы натяжения нити 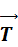и силы тяжести 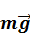привела к движению шарика с ускорением :

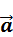откуда

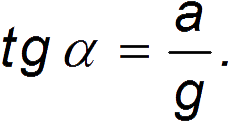
Так выглядит описание явления с точки зрения наблюдателя в инерциальной системе отсчета К (рис. 4.1).

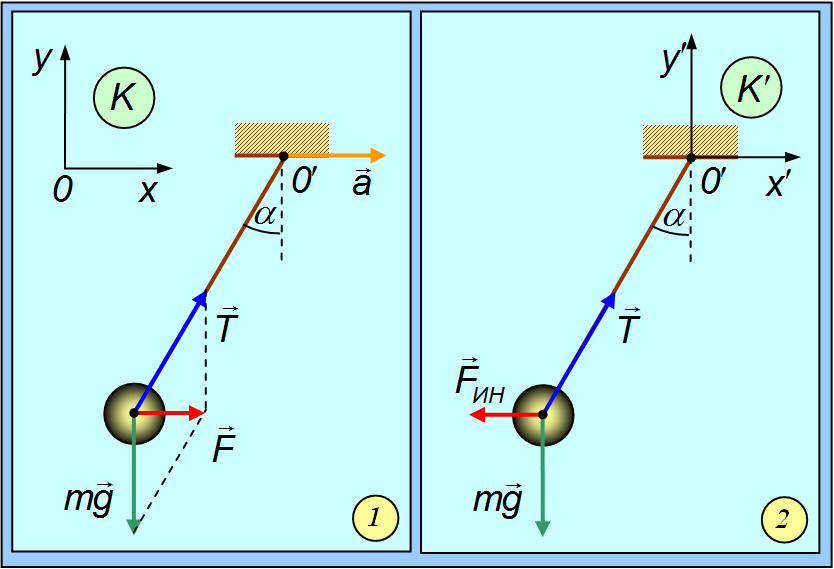
Рис. 4.1. Движение шарика на нити, точка подвеса которого движется с ускорением: 1 — с точки зрения наблюдателя в инерциальной системе отсчета; 2 — с точки зрения наблюдателя в движущейся неинерциальной системе отсчета

Свяжем теперь систему отсчета К' с точкой подвеса 0'. Эта система будет неинерциальной, так как она движется с ускорением 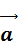относительно инерциальной системы К.

Мы пользуемся нерелятивистской механикой, так что угол отклонения нити, равно как и силы , для обоих наблюдателей одинаковы. Но для наблюдателя К' шарик находится в покое.

С другой стороны, наблюдатель К' видит, что результирующая сил 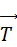и 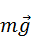не равна нулю. Поэтому наблюдатель К' приходит к выводу, что в его системе отсчета действует какая-то сила — сила инерции 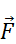_ин , которой не было в инерциальной системе отсчета К. Выражение для силы инерции получаем из условия равновесия шарика в системе К', то есть из равенства нулю трех сил:

Отсюда

и из уравнения второго закона Ньютона для тела следует выражение для силы инерции при поступательном движении неинерциальной системы отсчета с ускорением a:

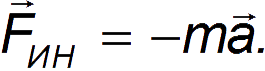
Центробежная сила инерции

Представим себе диск, равномерно вращающийся с угловой скоростью ω. Вместе с диском вращается надетый на спицу шарик, соединенный с центром диска пружиной (рис. 8.3).

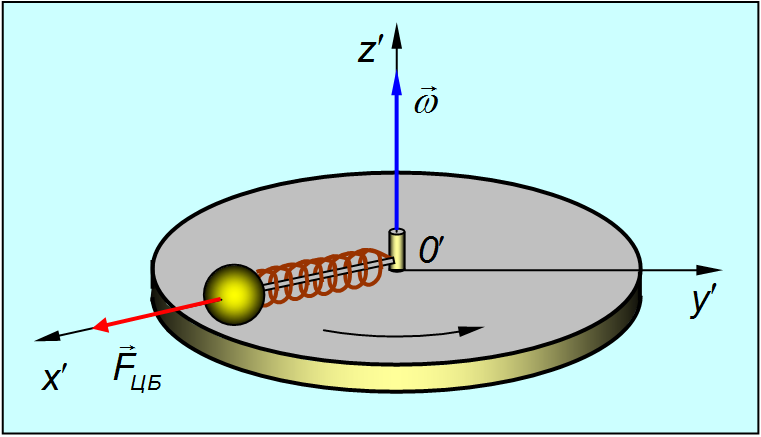
Рис. 4.3. Центробежная сила инерции в системе отсчета, связанной с вращающимся диском

Шарик покоится относительно диска и занимает на спице такое положение, при котором сила натяжения пружины F _пр оказывается равной произведению массы шарика m на нормальное (центростремительное) ускорение (при равномерном вращении диска тангенциальное ускорение шарика, очевидным образом, равно нулю)

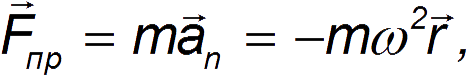
где — радиус-вектор, проведенный к шарику из центра диска (см. рис. 8.3).

Но так рассуждает наблюдатель, смотрящий на вращение диска из инерциальной системы отсчета.

Свяжем с диском вращающуюся неинерциальную систему отсчета К', в которой диск вместе с шариком покоится. Условие равновесия шарика в этой системе имеет вид:

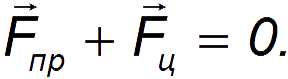
Наблюдатель во вращающейся системе отсчета объясняет равновесие шарика наличием силы инерции

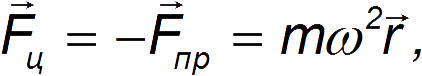
направленной от центра диска 0' по радиус-вектору .

Сила инерции, действующая на материальную точку в равномерно вращающейся с угловой скоростью ω системе отсчета, называется центробежной силой инерции:

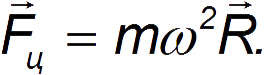
Здесь — вектор, проведенный к материальной точке от оси вращения ортогонально последней. Мы ввели его, чтобы отличить от радиус-вектора в том случае, когда начало координат лежит на оси вращения, но не в плоскости вращения материальной точки.

Сила Кориолиса

В предыдущем параграфе было рассмотрено тело, неподвижное во вращающейся системе отсчета. Если во вращающейся системе отсчета тело движется, то, помимо центробежной силы, на него будет действовать ещё одна сила инерции, называемая силой Кориолиса или кориолисовой силой инерции.

Пусть шарик массой движется без трения вдоль радиуса диска (рис. 8.5) с постоянной скоростью , направленной в некую точку на краю диска.

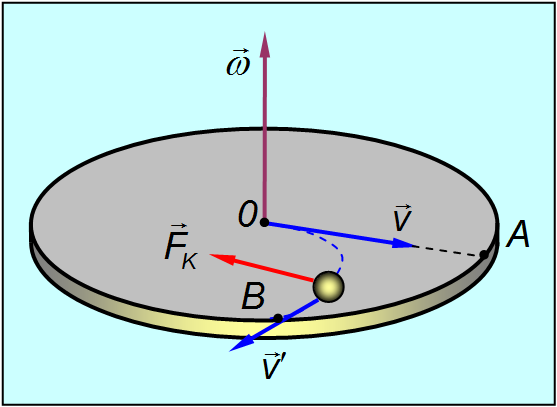
Рис. 4.5. Отклонение шарика, движущегося во вращающейся системе отсчета

Если диск не вращается, то шарик движется по радиусу и попадает в точку А. Если же диск привести во вращение с угловой скоростью ω, то к моменту достижения шариком края диска на месте точки А окажется другая точка В.

Если шарик оставляет след, то он прочертит свою траекторию относительно диска — кривую линию ОВ.

При этом на шарик не действуют никакие видимые силы, и относительно инерциальной системы он по-прежнему движется с постоянной скоростью .

Однако скорость шарика относительно диска изменяла свое направление. Значит, в системе отсчета, связанной с вращающимся диском, на шарик действовала сила инерции, не параллельная скорости .

Эта сила не была направлена по радиусу, откуда следует, что эта сила отлична от рассмотренной выше центробежной силы инерции. Ее и называют силой Кориолиса.

Найдем выражение для силы Кориолиса в частном случае (рис. 8.7), когда частица массой движется относительно вращающейся системы отсчета К' равномерно по окружности, лежащей в плоскости, перпендикулярной к оси вращения , с центром на оси вращения.

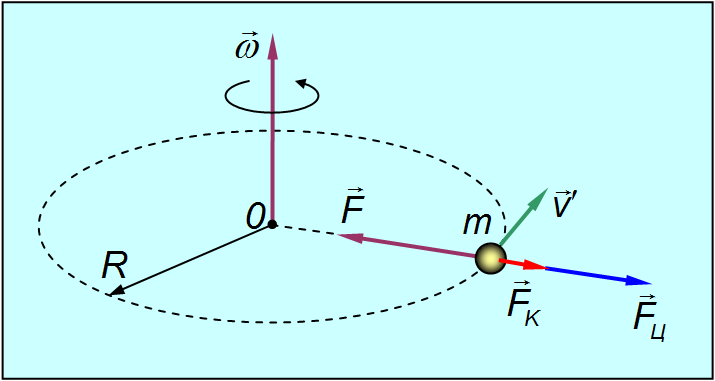
Рис. 4.6 К выводу выражения для силы Кориолиса

Скорость частицы относительно вращающейся системы К' обозначим через . В неподвижной (инерциальной) системе отсчета К частица также движется по окружности, но ее линейная скорость равна

где — угловая скорость вращающейся системы, R — радиус окружности. Для того, чтобы частица двигалась относительно неподвижной системы отсчета K по окружности со скоростью v = v +ω R, на нее должна действовать направленная к центру окружности сила F (например, натяжение нити), причем величина этой силы равна

Относительно вращающейся системы отсчета K' в этом случае частица движется с ускорением

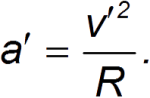
Из полученного выше уравнения второго закона Ньютона для частицы получаем:

Слева стоит произведение массы на ускорение частицы во вращающейся системе отсчета. Значит, справа должны стоять силы, на нее действующие. Первое слагаемое понятно: это сила натяжения нити, которая одинакова как для инерциальной, так и для неинерциальной систем. С третьим слагаемым мы тоже уже имели дело: это направленная по радиусу (от центра) центробежная сила инерции. Второе слагаемое и есть сила Кориолиса. В данном случае она также направлена от центра, но зависит от скорости частицы. Модуль кориолисовой силы в этом примере равен 2 mv ' ω . Ее направление совпадает с движением штопора, ручка которого поворачивается от вектора скорости v ' к вектору угловой скорости ω.

Можно показать, что в общем случае сила Кориолиса определяется как

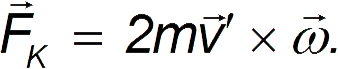
Сила Кориолиса ортогональна вектору скорости. В случае радиального движения, показанного на рис. 4.5, она отклоняла шарик направо, вынуждая его двигаться по траектории ОВ.

Возникновение силы Кориолиса при движении тела относительно вращающейся системы отсчета демонстрируется в опыте на рис. 4.6.

Сила Кориолиса действует только на тела, движущиеся относительно вращающейся системы отсчета, например, относительно Земли. Например в северном полушарии наблюдается более сильное подмывание правых берегов рек, правые рельсы железнодорожных путей по движению изнашиваются быстрее, чем левые, а циклоны вращаются по часовой стрелке. В южном же полушарии все происходит наоборот.

При выстреле из орудия, направленного на север, снаряд будет отклоняться к востоку в северном полушарии и к западу — в южном (рис. 4.7).

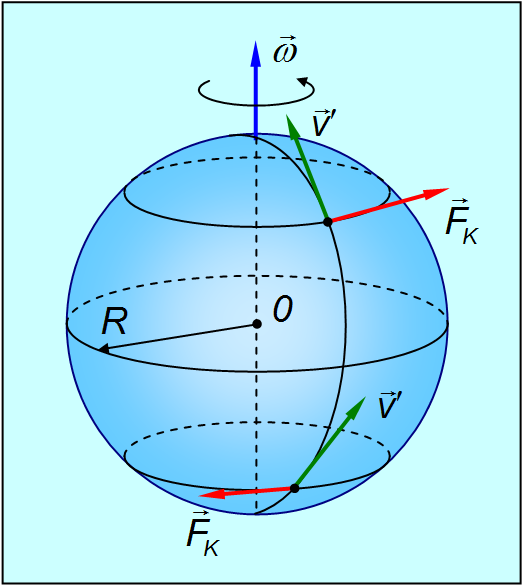
Рис. 4.7. На Земле движущиеся тела отклоняются направо в северном полушарии, и налево в южном

При стрельбе вдоль экватора силы Кориолиса будут прижимать снаряд к земле, если выстрел произведен на запад, и поднимать его кверху, если выстрел произведен в восточном направлении.

Французский физик Фуко экспериментально доказал вращение Земли вокруг своей оси с помощью 67-метрового маятника, подвешенного к вершине купола парижского Пантеона. Подобный маятник до недавнего времени можно было увидеть в Петербурге в Исаакиевском соборе.

Рис. 4.8. Маятник Фуко

Дата добавления: 2020-11-15; просмотров: 261; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!