Основные теоретические положения
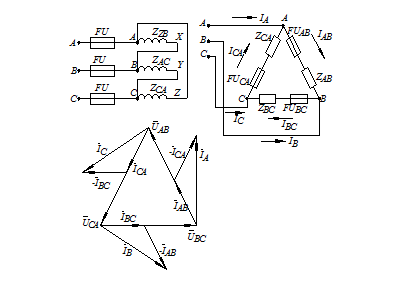
При выполнении соединения "треугольник" необходимо в первую очередь для каждого из трех однофазных потребителей установки соединить начало и конец. Например, для трехфазных катушек статора асинхронного электродвигателя (или трехфазного трансформатора) это будут соответственно А-Х, В- Y и С‑ Z. Далее, конец Х соединяется с началом В, Y с С, а Z с А. Образовавшиеся точки ХВ, YС, Z А присоединяются к линейным проводам А-А, В-В, С-С (рис. 1а).
а в
б
Рис. 1
Такое соединение более наглядно может быть показано в виде треугольника (рис. 1 б).
Каждый из однофазных потребителей определяется величинами полного сопротивления ZAB, ZBC, ZCA и коэффициента мощности cos φAB, cos φBC, cos φCA.
При равенстве полных сопротивлений фазных нагрузок и их коэффициентов мощности создается симметричная нагрузка соединения. Нарушения этих равенств создает несимметричную нагрузку.
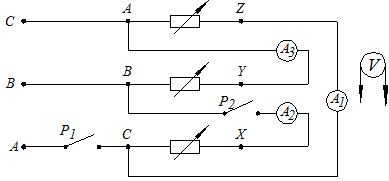
Рис. 2
Фазные потребители защищены от токов короткого замыкания плавкими предохранителями (F UAB, FUBC, FUBC). Короткое, замыкание в фазе АВ, например, приведет к плавлению предохранителя F UAB,что эквивалентно разрыву фазной нагрузки АВ.
На линейных проводах также установлены предохранители F UA, F UA, F UC. Плавление любого из них создает отключение соответствующего линейного провода.
С учетом этого в лабораторной работе изучаются следующие режимы работы соединения "треугольник":
1. Симметричный режим нагрузки фаз.
2. Несимметричный режим.
3. Режим обрыва фазы АВ.
4. Режим обрыва линейного провода А.
При соединении "треугольник" фазный потребитель подключен к двум линейным проводам, т.е. находится под линейные напряжением, которое одновременно является и фазным. Поэтому UФ= UЛ (рис. 2).
При установлении соотношения между фазными и линейными токами принято условие, что линейные токи направлены в условно положительном направлении от источника электрической энергии к потребителю, а фазные токи – от начала к концу фазного потребителя.
Применив 1-й закон Кирхгофа для узлов А Z, ВХ, С Y, можно легко получить следующие векторные уравнения:
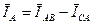 ;
;
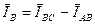 ; (1)
; (1)
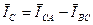 .
.
Каждый из фазных токов IАВ, IBC, ICA рассчитывается по модулю
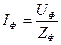 (2)
(2)
и по фазе
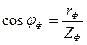 . (3)
. (3)
Например, для фазного потребителя AB
 ; (4)
; (4)
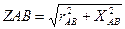 ; (5)
; (5)
 . (6)
. (6)
Очевидно, что для симметричной нагрузки фазные токи равны между собой:
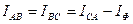 . (7)
. (7)
Линейные токи также равны между собой и превышают фазные в 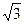 .
.
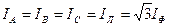 (8)
(8)
Эта зависимость вытекает из построения векторной диаграммы токов и напряжении при симметричной активной нагрузке (рис. 1 б). В этом случае фазные токи совпадают по направлению с фазными напряжениями, линейные токи определяются графически решением системы уравнений (1).
Несимметричная нагрузка связана с неравенством фазных токов (по модулю и фазе) и нарушением соотношения (8).
При разрыве цепи потребителя АВ ток
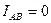 (9)
(9)
Потребители BC и СА остаются подключенными к линейным проводам под неизменным напряжением. Поэтому отключение потребителя АВ не повлияет на работу потребителей ВС и СА. Линейный ток IА станет равным фазному ICA, IB равным IBC. Линейный ток IC не изменится.
Обрыв линейного провода А окажет существенное влияние на режим работы соединения. В этом случае создаются две параллельные цепи, включенные под линейное напряжение – потребитель ВС и последовательное соединение потребителей ZAC, ZBC.
Фазный ток
 (10)
(10)
не изменится, а ток во второй цепи

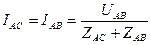 (11)
(11)
будет определяться суммой сопротивлений фазных нагрузок АС и АВ. Соответственно этому и распределение фазных напряжений UAC и UAB, будет зависеть от соотношения сопротивлений фазных потребителей АС и АВ. Поэтому такой режим работы соединения, нежелателен.
Порядок выполнения работы
1. Собрать схему соединения "треугольник" (рис. 2)
2. Включить рубильники Р1 и P2 и после проверки правильности соединений в схеме включить питание схемы.
3. Установить симметричная режим работы соединения. Это достигается соответствующим включением резисторов в каждой фазе. При этом амперметры фазных токов должны показывать одинаковые величины. С помощью вольтметра со щупами измерить линейные напряжения UAB, UBC, UCA. Показания записать в таблицу .
4. Установить несимметричный режим работы за счет изменения разных нагрузок. Измерить фазные и линейные величины, записать их в таблицу.
5. При несимметричном режиме (установленном в п.4) создать разрыв в фазе АВ. Для этого надо отключить P2, измерить фазные и линейные величину и записать их в таблицу.
6. Включить рубильник P2. При несимметричном режиме (установленном в п.4) выключить рубильник P1. Этим будет создан режим обрыва линейного провода А. Произвести измерения, записать их в таблицу.
Результаты измерений и вычислений
| Экспериментальные величины
| Расчетные величины
|
| Фазные токи, мА
| Напряжение, В
| Линейные токи мА
| Сопротивления фаз, Ом
|
| IAB
| IBC
| ICA
| UAB
| UBC
| UCA
| IA
| IB
| IC
| RAB
| RBC
| RCA
|
| | | | | | | | | | | | |
Примечания:
Опыт 1. Симметричная нагрузка, P1 и P2 включены;
Опыт 2. Несимметричная нагрузка, P1 и P2 включены;
Опыт 3. Несимметричная нагрузка, P1 – включен, P2 – отключен, разрыв фазы АВ;
Опыт 4. Несимметричная нагрузка, P1 – отключен, P2 – включен. Обрыв линейного провода А.
7. Найти отношение среднеарифметических значений линейных и фазных токов и сравнить их о теоретическим значением.
8. Рассчитать величины активной нагрузки в каждой фазе по формуле.
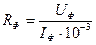 .
.
9. Для первых трех опытов построить в масштабе векторные диаграммы токов и напряжений. Определить по ним значения линейных токов и записать их в таблицу.
10. Сделать выводы по каждому исследованному режиму.
Контрольные вопросы и задания
1. Нарисуйте схему соединения "треугольник" для следующих потребителей: в фазе АВ – активно-индуктивная нагрузка, в фазе ВС – активная нагрузка, в фазе СА – активно-емкостная нагрузка.
2. Постройте векторную диаграмму токов и напряжений для этого случая.
3. Для трех фазных обмоток электродвигателя нужно произвести соединение "треугольник". Нарисуйте схему с указанием начала и конца фазных обмоток.
4. Постройте векторную диаграмму токов и напряжений для этого случая. Графически определите эти токи.
5. Какому режиму соответствует отключение рубильника P1 (или P2) при реальном использовании соединения "треугольник".
6. Как изменится активная мощность трехфазного асинхронного электродвигателя при переключении его обмоток со "звезды" на "треугольник" при сохранении величины линейного напряжения.
7. Можно ли допустить длительную эксплуатацию фазных потребителей, соединенных треугольником, при обрыве одного из линейных проводов?
8. Расскажите о ходе выполнения лабораторной работы.
9. Соберите схему лабораторной установки.
Литература
1. Кононенко В.В. и др. Электротехника и электроника: Учебное пособие для вузов. Серия "Высшее образование", 2-е изд. – Ростов н/Д: Феникс, 2006.
2. Методические указания к лабораторной работе по курсу "Общая электротехника" /Г.С.Селезнев, И.М. Эршон, А.П. Мальков, Н.Л. Быкадорова, В.В.Кононенко.– Ростов н/Д: РИСИ, 1972.
3. Методические указания к лабораторным работам по электротехнике /В.В.Кононенко, Н.В.Кузнецов, В.Е. Столярчук, Т.С.Иванова, В.И. Ми-
шкович, Ю.П. Шагинян. Часть 1. II-е изд. – Ростов н/Д: РИСИ, 1981.
4. Электротехника /Под ред. В.Г. Герасимова. – М.: Высшая школа, 1985.
5. ГОСТ 2.721-74 ÷ ГОСТ 2.766-76. Обозначения условные графические в электрических схемах.
Редактор Н.Е. Гладких
Темплан 2007 г.,поз. 87________________________________________________
Подписано в печать 26.04.07 Формат 60х84 1/16.
Бумага писчая. Ризограф. Уч.-изд.л. 2.0. Тираж 250 экз.
Зказ_________________________________________________________________
Редакционно-издательский центр
Ростовского государственного строительного университета
344022, Ростов-на-Дону, ул. Социалистическая, 162
| Министерство образования и науки РФ
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
"Ростовский государственный строительный университет"
"Утверждено"
на заседании кафедры
ЭЛА
28 февраля 2007 г.
Методические указания
к лабораторным работам по электротехнике
Часть 1
(Издание VII, переработанное)
Ростов-на-Дону, 2007
УДК 621.3
| |
| | | | | | | |
| | | | |
|
| | Методические указания к лабораторным работам по электротехнике. Часть I. (изд. VII перераб.). - Ростов н/Д: Рост. гос. строит. ун-т, 2007. - 32 с.
Приведены методические указания по выполнению лабораторных работ по I части курса электротехники. Рассматриваются сложное соединение, двухпроводная линия электропередач, последовательное и параллельное соединение элементов в однофазной цепи, а также схемы соединения треугольником и звездой в трехфазных цепях.
Предназначены для студентов строительных специальностей РГСУ и могут быть использованы при изучении курсов электротехнического профиля.
Составители: В.В. Кононенко
В.И. Мишкович
В.Ю.Бобыльченко
© Ростовский государственный строительный университет, 2007
Лабораторная работа № 1
| | | |
Редактор Н.Е. Гладких
Темплан 2007 г.,поз. 87________________________________________________
Подписано в печать 26.04.07 Формат 60х84 1/16.
Бумага писчая. Ризограф. Уч.-изд.л. 2.0. Тираж 250 экз.
Зказ_________________________________________________________________
Редакционно-издательский центр
Ростовского государственного строительного университета
344022, Ростов-на-Дону, ул. Социалистическая, 162
| |
| | | | | | | |
| | | | |
|
| | 1. Нарисуйте схему соединения "треугольник" для следующих потребителей: в фазе АВ – активно-индуктивная нагрузка, в фазе ВС – активная нагрузка, в фазе СА – активно-емкостная нагрузка.
2. Постройте векторную диаграмму токов и напряжений для этого случая.
3. Для трех фазных обмоток электродвигателя нужно произвести соединение "треугольник". Нарисуйте схему с указанием начала и конца фазных обмоток.
4. Постройте векторную диаграмму токов и напряжений для этого случая. Графически определите эти токи.
5. Какому режиму соответствует отключение рубильника P1 (или P2) при реальном использовании соединения "треугольник".
6. Как изменится активная мощность трехфазного асинхронного электродвигателя при переключении его обмоток со "звезды" на "треугольник" при сохранении величины линейного напряжения.
7. Можно ли допустить длительную эксплуатацию фазных потребителей, соединенных треугольником, при обрыве одного из линейных проводов?
8. Расскажите о ходе выполнения лабораторной работы.
9. Соберите схему лабораторной установки.
Литература
1. Кононенко В.В. и др. Электротехника и электроника: Учебное пособие для вузов. Серия "Высшее образование", 2-е изд. – Ростов н/Д: Феникс, 2006.
2. Методические указания к лабораторной работе по курсу "Общая электротехника" /Г.С.Селезнев, И.М. Эршон, А.П. Мальков, Н.Л. Быкадорова, В.В.Кононенко.– Ростов н/Д: РИСИ, 1972.
3. Методические указания к лабораторным работам по электротехнике /В.В.Кононенко, Н.В.Кузнецов, В.Е. Столярчук, Т.С.Иванова, В.И. Ми-
шкович, Ю.П. Шагинян. Часть 1. II-е изд. – Ростов н/Д: РИСИ, 1981.
4. Электротехника /Под ред. В.Г. Герасимова. – М.: Высшая школа, 1985.
5. ГОСТ 2.721-74 ÷ ГОСТ 2.766-76. Обозначения условные графические в электрических схемах.
| | | Электрическая цепь с одним источником питания и смешанным соединением элементов
Цель работы: 1) изучить способ соединения приемников электрической энергии; 2) проверить опытным путем законы Ома и Кирхгофа.
Основные теоретические положения
Основными, элементами любой электрической цепи являются:
а) источкики электрической энергии (электромашинные генераторы, аккумуляторные батареи, термоэлементы и т.д.);
б) передающие устройства (линии электропередачи);
в) приемники электрической энергии (нагревательные элементы, осветительные приборы, электрические двигатели и т.д.).
Как правило, в электрическую цепь включаются устроиства защиты и управления (плавкие предохранители, автоматические выключатели, магнитные пускатели, рубильники и т.д.).
При необходимости она может быть снабжена преобразующими элементами (повышающими и понижающими напряжение трансформаторами, выпрямителями, инверторами и т.д.), а также контрольно-измерительными приборами (амперметрами, вольтметрами и т.д.).
Расчет и анализ электрических цепей может быть проведен с помощью законов Ома и Кирхгофа, являющихся основными законами электротехники.
С помощью закона Ома описывается связь между током, напряжением и сопротивлением заданного участка цепи
 .
При составлении уравнений по законам Кирхгофа необходимо предварительно задаться положительными направлениями токов и напряжений. При этом нужно учитывать, что в приемниках электрической энергии напряжение и ток направлены в одну сторону, а в источниках питания - в противоположную.
Согласно 1-му закону Кирхгофа, алгебраическая сумма токов, сходящихся в любом узле цепи, равна нулю, т.е. .
При составлении уравнений по законам Кирхгофа необходимо предварительно задаться положительными направлениями токов и напряжений. При этом нужно учитывать, что в приемниках электрической энергии напряжение и ток направлены в одну сторону, а в источниках питания - в противоположную.
Согласно 1-му закону Кирхгофа, алгебраическая сумма токов, сходящихся в любом узле цепи, равна нулю, т.е.
 .
Со знаком "+" в это уравнение следует включать токи, направленные к узлу, а со знаком "-" – токи, отходящие от узла (допускается и наоборот).
С помощью этого закона может быть описано, например, электрическое состояние схемы, представляющее собой параллельное соединение элементов и показанное на рис. 1 а. .
Со знаком "+" в это уравнение следует включать токи, направленные к узлу, а со знаком "-" – токи, отходящие от узла (допускается и наоборот).
С помощью этого закона может быть описано, например, электрическое состояние схемы, представляющее собой параллельное соединение элементов и показанное на рис. 1 а.
 или или  . .
| |
| | | | | | | |
| | | | |
|
|  Рис. 1. Параллельное соединение элементов:
а – общая схема; б – включение нагревательного элемента (НЭ), двигателя (М) вентилятора и ламп накаливания (Л); в- включение амперметра с шунтом.
Так как при параллельном соединении все элементы находятся под одним и тем же напряжением, то, используя закон Ома, это уравнение можно записать в виде Рис. 1. Параллельное соединение элементов:
а – общая схема; б – включение нагревательного элемента (НЭ), двигателя (М) вентилятора и ламп накаливания (Л); в- включение амперметра с шунтом.
Так как при параллельном соединении все элементы находятся под одним и тем же напряжением, то, используя закон Ома, это уравнение можно записать в виде
 ; ;  ; ;  ,
где RЭ и gЭ – эквивалентные сопротивление и проводимость данной цепи соответственно.
Благодаря тому, что параллельное соединение обеспечивает одинаковое напряжение на всех приемниках, оно нашло широкое распространение в практической электротехнике.
Так, например, параллельно включаются осветительные устройства, нагревательные элементы, радио- и телеаппаратура, холодильники и др. электроприемники в жилых домах (рис. 1 б).
Нередко такое соединение используется для расширения пределов измерения амперметров (рис. 1 в) и в других случаях.
По 2-му закону Кирхгофа алгебраическая сумма напряжений всех участков замкнутого контура равна нулю: ,
где RЭ и gЭ – эквивалентные сопротивление и проводимость данной цепи соответственно.
Благодаря тому, что параллельное соединение обеспечивает одинаковое напряжение на всех приемниках, оно нашло широкое распространение в практической электротехнике.
Так, например, параллельно включаются осветительные устройства, нагревательные элементы, радио- и телеаппаратура, холодильники и др. электроприемники в жилых домах (рис. 1 б).
Нередко такое соединение используется для расширения пределов измерения амперметров (рис. 1 в) и в других случаях.
По 2-му закону Кирхгофа алгебраическая сумма напряжений всех участков замкнутого контура равна нулю:
 или или  .
При составлении уравнений по этому закону слагаемые берут со знаком "+", когда произвольно выбранное направление обхода контура совпадает с направлением U или I. В противном случае слагаемые берут со знаком "-". Например, для цепи, показанной на рис. 2 а .
При составлении уравнений по этому закону слагаемые берут со знаком "+", когда произвольно выбранное направление обхода контура совпадает с направлением U или I. В противном случае слагаемые берут со знаком "-". Например, для цепи, показанной на рис. 2 а
 или или  . .
| | |
Порядок выполнения работы
1. Собрать схему соединения "треугольник" (рис. 2)
2. Включить рубильники Р1 и P2 и после проверки правильности соединений в схеме включить питание схемы.
3. Установить симметричная режим работы соединения. Это достигается соответствующим включением резисторов в каждой фазе. При этом амперметры фазных токов должны показывать одинаковые величины. С помощью вольтметра со щупами измерить линейные напряжения UAB, UBC, UCA. Показания записать в таблицу .
4. Установить несимметричный режим работы за счет изменения разных нагрузок. Измерить фазные и линейные величины, записать их в таблицу.
5. При несимметричном режиме (установленном в п.4) создать разрыв в фазе АВ. Для этого надо отключить P2, измерить фазные и линейные величину и записать их в таблицу.
6. Включить рубильник P2. При несимметричном режиме (установленном в п.4) выключить рубильник P1. Этим будет создан режим обрыва линейного провода А. Произвести измерения, записать их в таблицу.
Результаты измерений и вычислений
| Экспериментальные величины
| Расчетные величины
| | Фазные токи, мА
| Напряжение, В
| Линейные токи мА
| Сопротивления фаз, Ом
| | IAB
| IBC
| ICA
| UAB
| UBC
| UCA
| IA
| IB
| IC
| RAB
| RBC
| RCA
| | | | | | | | | | | | | | Примечания:
Опыт 1. Симметричная нагрузка, P1 и P2 включены;
Опыт 2. Несимметричная нагрузка, P1 и P2 включены;
Опыт 3. Несимметричная нагрузка, P1 – включен, P2 – отключен, разрыв фазы АВ;
Опыт 4. Несимметричная нагрузка, P1 – отключен, P2 – включен. Обрыв линейного провода А.
7. Найти отношение среднеарифметических значений линейных и фазных токов и сравнить их о теоретическим значением.
8. Рассчитать величины активной нагрузки в каждой фазе по формуле.
 . .
9. Для первых трех опытов построить в масштабе векторные диаграммы токов и напряжений. Определить по ним значения линейных токов и записать их в таблицу.
10. Сделать выводы по каждому исследованному режиму.
Контрольные вопросы и задания
| |
| | | | | | | |
| | | | |
|
|  . (3)
Например, для фазного потребителя AB . (3)
Например, для фазного потребителя AB
 ; (4) ; (4)
 ; (5) ; (5)
 . (6)
Очевидно, что для симметричной нагрузки фазные токи равны между собой: . (6)
Очевидно, что для симметричной нагрузки фазные токи равны между собой:
 . (7)
Линейные токи также равны между собой и превышают фазные в . (7)
Линейные токи также равны между собой и превышают фазные в  . .
 (8)
Эта зависимость вытекает из построения векторной диаграммы токов и напряжении при симметричной активной нагрузке (рис. 1 б). В этом случае фазные токи совпадают по направлению с фазными напряжениями, линейные токи определяются графически решением системы уравнений (1).
Несимметричная нагрузка связана с неравенством фазных токов (по модулю и фазе) и нарушением соотношения (8).
При разрыве цепи потребителя АВ ток (8)
Эта зависимость вытекает из построения векторной диаграммы токов и напряжении при симметричной активной нагрузке (рис. 1 б). В этом случае фазные токи совпадают по направлению с фазными напряжениями, линейные токи определяются графически решением системы уравнений (1).
Несимметричная нагрузка связана с неравенством фазных токов (по модулю и фазе) и нарушением соотношения (8).
При разрыве цепи потребителя АВ ток
 (9)
Потребители BC и СА остаются подключенными к линейным проводам под неизменным напряжением. Поэтому отключение потребителя АВ не повлияет на работу потребителей ВС и СА. Линейный ток IА станет равным фазному ICA, IB равным IBC. Линейный ток IC не изменится.
Обрыв линейного провода А окажет существенное влияние на режим работы соединения. В этом случае создаются две параллельные цепи, включенные под линейное напряжение – потребитель ВС и последовательное соединение потребителей ZAC, ZBC.
Фазный ток (9)
Потребители BC и СА остаются подключенными к линейным проводам под неизменным напряжением. Поэтому отключение потребителя АВ не повлияет на работу потребителей ВС и СА. Линейный ток IА станет равным фазному ICA, IB равным IBC. Линейный ток IC не изменится.
Обрыв линейного провода А окажет существенное влияние на режим работы соединения. В этом случае создаются две параллельные цепи, включенные под линейное напряжение – потребитель ВС и последовательное соединение потребителей ZAC, ZBC.
Фазный ток
 (10)
не изменится, а ток во второй цепи (10)
не изменится, а ток во второй цепи
  (11)
будет определяться суммой сопротивлений фазных нагрузок АС и АВ. Соответственно этому и распределение фазных напряжений UAC и UAB, будет зависеть от соотношения сопротивлений фазных потребителей АС и АВ. Поэтому такой режим работы соединения, нежелателен. (11)
будет определяться суммой сопротивлений фазных нагрузок АС и АВ. Соответственно этому и распределение фазных напряжений UAC и UAB, будет зависеть от соотношения сопротивлений фазных потребителей АС и АВ. Поэтому такой режим работы соединения, нежелателен.
| | |  Рис. 2. Последовательное соединение элементов:
а – общая схема; б – схема расширения пределов измерения; в – схема генератора постоянного тока
Так как при последовательном соединении по всем элементам протекает один и тот же ток, то, используя закон Ома, можно записать Рис. 2. Последовательное соединение элементов:
а – общая схема; б – схема расширения пределов измерения; в – схема генератора постоянного тока
Так как при последовательном соединении по всем элементам протекает один и тот же ток, то, используя закон Ома, можно записать
 или или  .
Приемники электрической энергии последовательно соединяются относительно редко, т.к. исключается возможность независимого их включения и отключения, а при выходе из строя одного из приемников отключаются и все остальные.
В качестве примера можно привести схему генератора постоянного тока последовательного возбуждения (рис. 2 в). В измерительной технике последовательным включением добавочных резисторов расширяют пределы измерения вольтметров (рис. 2 б) и т.п.
Сложным (смешанным) соединением называют электрические цепи, в состав которых входят последовательно и параллельно соединенные участки.
К такому соединению относится и схема лабораторной установки, показанной на рис. 3. .
Приемники электрической энергии последовательно соединяются относительно редко, т.к. исключается возможность независимого их включения и отключения, а при выходе из строя одного из приемников отключаются и все остальные.
В качестве примера можно привести схему генератора постоянного тока последовательного возбуждения (рис. 2 в). В измерительной технике последовательным включением добавочных резисторов расширяют пределы измерения вольтметров (рис. 2 б) и т.п.
Сложным (смешанным) соединением называют электрические цепи, в состав которых входят последовательно и параллельно соединенные участки.
К такому соединению относится и схема лабораторной установки, показанной на рис. 3.
 Рис. 3. Схема лабораторной установки
Электрическое состояние этой схемы описывается следующими уравнениями Рис. 3. Схема лабораторной установки
Электрическое состояние этой схемы описывается следующими уравнениями
 ; ;  .
Порядок выполнения работы
1. Собрать схему лабораторной установки (рис .3). .
Порядок выполнения работы
1. Собрать схему лабораторной установки (рис .3).
| |
| | | | | | | |
| | | | |
|
| 2. Установить с помощью тумблеров различные значения сопротивлений R1, R2, R3 (три комбинации), измерить токи и напряжения на отдельных участках цепи. Полученные данные занести в таблицу.
Результаты измерений и расчетов
| № п/п
| Измерено
| Вычислено
| | Токи, мА*
| Напряжения, В
| Сопротивления, Ом
| | I1
| I2
| I3
| U
| UАД
| UДЕ
| R1
| R2
| R3
| RЭ
| R'Э
| | | | | | | | | | | | | | *Примечание. При проведении расчетов величину токов переводить в амперы: 1 мА=10-3 А
3. Используя закон Ома, вычислить для всех опытов сопротивления резисторов R1, R2, R3, а также значение эквивалентного сопротивления цепи (двумя способами):
 (1-й способ); (1-й способ);  (2-й способ). (2-й способ).
4. Проанализировать полученные результаты и записать выводы в отсчет.
Контрольные вопросы и задания
1. Какое соединение называется последовательным, параллельным, смешанным?
2. Сформулируйте закон Ома для участка цепи.
3. Сформулируйте 1-й и 2-й законы Кирхгофа.
4. Как изменятся показания всех приборов схемы, если при неизменных R2, R3, U:
а) уменьшить R1;
б) увеличить R1;
5. Назовите единицы измерения тока, напряжения, ЭДС, сопротивления, проводимости.
6. Что такое электрический ток, напряжение, ЭДС, сопротивление, проводимость?
7. Расскажите о порядке выполнения лабораторной работы.
8. Соберите схему лабораторной установки.
Лабораторная работа № 2
Исследование работы двухпроводной линии электропередачи
Цель работы:
1) познакомиться с основными электротехническими параметрами, характеризующими работу линии электропередачи (ЛЭП);
2) исследовать работу линии в режиме холостого хода нагрузки;
| | |  Рис. 2
Фазные потребители защищены от токов короткого замыкания плавкими предохранителями (F UAB, FUBC, FUBC). Короткое, замыкание в фазе АВ, например, приведет к плавлению предохранителя F UAB,что эквивалентно разрыву фазной нагрузки АВ.
На линейных проводах также установлены предохранители F UA, F UA, F UC. Плавление любого из них создает отключение соответствующего линейного провода.
С учетом этого в лабораторной работе изучаются следующие режимы работы соединения "треугольник":
1. Симметричный режим нагрузки фаз.
2. Несимметричный режим.
3. Режим обрыва фазы АВ.
4. Режим обрыва линейного провода А.
При соединении "треугольник" фазный потребитель подключен к двум линейным проводам, т.е. находится под линейные напряжением, которое одновременно является и фазным. Поэтому UФ= UЛ (рис. 2).
При установлении соотношения между фазными и линейными токами принято условие, что линейные токи направлены в условно положительном направлении от источника электрической энергии к потребителю, а фазные токи – от начала к концу фазного потребителя.
Применив 1-й закон Кирхгофа для узлов А Z, ВХ, С Y, можно легко получить следующие векторные уравнения:
Рис. 2
Фазные потребители защищены от токов короткого замыкания плавкими предохранителями (F UAB, FUBC, FUBC). Короткое, замыкание в фазе АВ, например, приведет к плавлению предохранителя F UAB,что эквивалентно разрыву фазной нагрузки АВ.
На линейных проводах также установлены предохранители F UA, F UA, F UC. Плавление любого из них создает отключение соответствующего линейного провода.
С учетом этого в лабораторной работе изучаются следующие режимы работы соединения "треугольник":
1. Симметричный режим нагрузки фаз.
2. Несимметричный режим.
3. Режим обрыва фазы АВ.
4. Режим обрыва линейного провода А.
При соединении "треугольник" фазный потребитель подключен к двум линейным проводам, т.е. находится под линейные напряжением, которое одновременно является и фазным. Поэтому UФ= UЛ (рис. 2).
При установлении соотношения между фазными и линейными токами принято условие, что линейные токи направлены в условно положительном направлении от источника электрической энергии к потребителю, а фазные токи – от начала к концу фазного потребителя.
Применив 1-й закон Кирхгофа для узлов А Z, ВХ, С Y, можно легко получить следующие векторные уравнения:
 ; ;
 ; (1) ; (1)
 .
Каждый из фазных токов IАВ, IBC, ICA рассчитывается по модулю .
Каждый из фазных токов IАВ, IBC, ICA рассчитывается по модулю
 (2)
и по фазе (2)
и по фазе
| |
| | | | | | | |
| | | | |
|
|
Цель работы: l) установить соотношения между фазными и линейными величинами токов и напряжений при различных режимах работы соединения; 2) по опытным данным построить векторные диаграммы токов и напряжений при симметричной и несимметричной нагрузках фаз; З) выяснить влияние обрыва линейного провода и разрыва в фазе на режим работы потребителей.
Основные теоретические положения
При выполнении соединения "треугольник" необходимо в первую очередь для каждого из трех однофазных потребителей установки соединить начало и конец. Например, для трехфазных катушек статора асинхронного электродвигателя (или трехфазного трансформатора) это будут соответственно А-Х, В- Y и С‑ Z. Далее, конец Х соединяется с началом В, Y с С, а Z с А. Образовавшиеся точки ХВ, YС, Z А присоединяются к линейным проводам А-А, В-В, С-С (рис. 1а).
а в
 б
Рис. 1
Такое соединение более наглядно может быть показано в виде треугольника (рис. 1 б).
Каждый из однофазных потребителей определяется величинами полного сопротивления ZAB, ZBC, ZCA и коэффициента мощности cos φAB, cos φBC, cos φCA.
При равенстве полных сопротивлений фазных нагрузок и их коэффициентов мощности создается симметричная нагрузка соединения. Нарушения этих равенств создает несимметричную нагрузку.
б
Рис. 1
Такое соединение более наглядно может быть показано в виде треугольника (рис. 1 б).
Каждый из однофазных потребителей определяется величинами полного сопротивления ZAB, ZBC, ZCA и коэффициента мощности cos φAB, cos φBC, cos φCA.
При равенстве полных сопротивлений фазных нагрузок и их коэффициентов мощности создается симметричная нагрузка соединения. Нарушения этих равенств создает несимметричную нагрузку.
| | | 3) исследовать влияние тока нагрузки на потерю напряжения и мощности, а также коэффициент полезного действия линии.
Основные теоретические положения
Передача и распределение электрической энергии осуществляется в большинстве случаев с помощью воздушных и кабельных линий электропередачи. Однолинейная, принципиальная схема производства, передачи и распределения электроэнергии показана на рис. 1.
На строительных площадках получили широкое распространение воздушные линии (ВЛ) вследствие возможности простого изменения трассы в ходе строительных работ, их меньшей стоимости (по сравнению с кабельными), простоты обнаружения мест повреждения, а также удобства ремонта.
 Рис.1. Принципиальная схема производства, передачи и распределения электроэнергии:
1-трехфазный генератор электростанции; 2-трансформаторная подстанция (ТП) с повышающим трансформатором; 3-воздушная линия электроснабжения (ЛЭП); 4-главная понижающая подстанция; 5-ТП с поникающим трансформатором; 6-кабепьнае воздушные распределительные линии электроснабжения; 7-ТП3 и ТП4 - трансформаторные подстанции потребителей электроэнергии; 8-приемники электроэнергии.
В условиях предприятии стройиндустрии, как и вообще промышленных предприятий, а также в жилых районах и на стройплощадках, распределение электроэнергии осуществляется и кабельными линиями (КЛ), которые отличаются высокой надежностью электроснабжения. Они не подвержены влиянию ветра и гололеда, не загромождают, подобно ВЛ, улицы ropoда и территории предприятий
При передаче электроэнергии от электростанции к потребителю, т.е. при прохождении по проводам электрического тока, в ЛЭП возникает потеря напряжения, под которой понимают разность напряжений в начале U1 и в конце U2 линии:
Рис.1. Принципиальная схема производства, передачи и распределения электроэнергии:
1-трехфазный генератор электростанции; 2-трансформаторная подстанция (ТП) с повышающим трансформатором; 3-воздушная линия электроснабжения (ЛЭП); 4-главная понижающая подстанция; 5-ТП с поникающим трансформатором; 6-кабепьнае воздушные распределительные линии электроснабжения; 7-ТП3 и ТП4 - трансформаторные подстанции потребителей электроэнергии; 8-приемники электроэнергии.
В условиях предприятии стройиндустрии, как и вообще промышленных предприятий, а также в жилых районах и на стройплощадках, распределение электроэнергии осуществляется и кабельными линиями (КЛ), которые отличаются высокой надежностью электроснабжения. Они не подвержены влиянию ветра и гололеда, не загромождают, подобно ВЛ, улицы ropoда и территории предприятий
При передаче электроэнергии от электростанции к потребителю, т.е. при прохождении по проводам электрического тока, в ЛЭП возникает потеря напряжения, под которой понимают разность напряжений в начале U1 и в конце U2 линии:
| |
| | | | | | | |
| | | | |
|
|  (1)
Потеря напряжения может быть определена и таким образом (1)
Потеря напряжения может быть определена и таким образом
 (2)
где I - величина токе в линии передачи;
R - сопротивление проводов линии.
Необходимо отметить, что потеря напряжения в ЛЭП ухудшает работу электроприемников. Так, при уменьшении напряжения на 10% от номинального, световой поток ламп снижается на 30%. Поскольку вращающий момент на валy асинхронных двигателей пропорционален квадрату напряжения на его зажимах, то он значительно уменьшается при снижении питающего напряжения. А это отрицательно сказывается на работе производственных механизмов.
ГОСТом нормируются допустимые отклонения напряжения в проц.:
а) на зажимах приборов рабочего освещения, в т.ч. и прожекторного, от ‑2,5 до +5 % от номинального;
б) не электродвигателях от -5 до +10% от номинального;
в) на зажимах остальных приемников электрической энергии в пределах ±5% от номинального.
В связи с этим потерю напряжения, при расчетах выражают часто не в вольтах, а в процентах (2)
где I - величина токе в линии передачи;
R - сопротивление проводов линии.
Необходимо отметить, что потеря напряжения в ЛЭП ухудшает работу электроприемников. Так, при уменьшении напряжения на 10% от номинального, световой поток ламп снижается на 30%. Поскольку вращающий момент на валy асинхронных двигателей пропорционален квадрату напряжения на его зажимах, то он значительно уменьшается при снижении питающего напряжения. А это отрицательно сказывается на работе производственных механизмов.
ГОСТом нормируются допустимые отклонения напряжения в проц.:
а) на зажимах приборов рабочего освещения, в т.ч. и прожекторного, от ‑2,5 до +5 % от номинального;
б) не электродвигателях от -5 до +10% от номинального;
в) на зажимах остальных приемников электрической энергии в пределах ±5% от номинального.
В связи с этим потерю напряжения, при расчетах выражают часто не в вольтах, а в процентах
 (3)
Прохождение электрического тока по проводам линий электропередач приводит к необратимому преобразованию электрической энергии в тепловую, т.е. к их бесполезному нагреву. Этот нагрев происходит за счет потерь мощности Р в проводах (3)
Прохождение электрического тока по проводам линий электропередач приводит к необратимому преобразованию электрической энергии в тепловую, т.е. к их бесполезному нагреву. Этот нагрев происходит за счет потерь мощности Р в проводах
 (4)
которые можно определить и так: (4)
которые можно определить и так:
 (5)
Мощность Р1 (затраченная) подается на вход линии передачи от генератора и может быть определена из соотношения (5)
Мощность Р1 (затраченная) подается на вход линии передачи от генератора и может быть определена из соотношения
 (6)
Мощность Р2 (полезная) снимается с выхода линии и передается потребителям. Её величину рассчитывают, используя выражение (6)
Мощность Р2 (полезная) снимается с выхода линии и передается потребителям. Её величину рассчитывают, используя выражение
 (7)
Отношение этих мощностей называют коэффициентом полезного действия h (7)
Отношение этих мощностей называют коэффициентом полезного действия h
 (8)
который характеризует экономичность работы линии электропередачи. Современные ЛЭП обеспечивают передачу электрической энергии с h=95÷98 %. (8)
который характеризует экономичность работы линии электропередачи. Современные ЛЭП обеспечивают передачу электрической энергии с h=95÷98 %.
| | |  Рис. 4. Принципиальная электрическая схема стенда
г) построить в масштабе по опытным данным векторные диаграммы напряжения и токов для всех исследованных режимов работы трехфазной системы.
По результатам сделать выводы о соотношении между фазными и линейными величинами; о назначении нулевого провода; о работе соединения "звезда" при всех исследованных режимах.
Контрольные вопросы и задан
1. Как соединить потребители звездой ?
2. Какие напряжения и токи называются
а) фазными; б) линейными?
3. Запишите векторные уравнения, связывающие между собой фазные и линейные напряжения.
4. Каковы соотношения между а) фазными и линейными токами; б) фазными и линейными напряжениями при симметричной нагрузке?
5. Какие функции выполняет нулевой провод ?
6. Как отразится обрыв нулевого провода на работу потребителей при несимметричной нагрузке ?
7. Как изменятся напряжения потребителей при обрыве одного из линейных проводов и отсутствии нулевого провода?
8. Построите векторную диаграмму токов и напряжений при несимметричной активно-индуктивной нагрузке.
9. По каким формулам рассчитываются мощности соединения "звезда" при симметричной и несимметричной нагрузке ?
10. Приведите пример использования симметричной (несимметричной) нагрузки, соединенной звездой в технике.
11. Соберите схему лабораторной установки.
12. Расскажите порядок выполнения лабораторной работы.
Лабораторная работа № 6
Соединение приемника треугольником в трехфазной цепи Рис. 4. Принципиальная электрическая схема стенда
г) построить в масштабе по опытным данным векторные диаграммы напряжения и токов для всех исследованных режимов работы трехфазной системы.
По результатам сделать выводы о соотношении между фазными и линейными величинами; о назначении нулевого провода; о работе соединения "звезда" при всех исследованных режимах.
Контрольные вопросы и задан
1. Как соединить потребители звездой ?
2. Какие напряжения и токи называются
а) фазными; б) линейными?
3. Запишите векторные уравнения, связывающие между собой фазные и линейные напряжения.
4. Каковы соотношения между а) фазными и линейными токами; б) фазными и линейными напряжениями при симметричной нагрузке?
5. Какие функции выполняет нулевой провод ?
6. Как отразится обрыв нулевого провода на работу потребителей при несимметричной нагрузке ?
7. Как изменятся напряжения потребителей при обрыве одного из линейных проводов и отсутствии нулевого провода?
8. Построите векторную диаграмму токов и напряжений при несимметричной активно-индуктивной нагрузке.
9. По каким формулам рассчитываются мощности соединения "звезда" при симметричной и несимметричной нагрузке ?
10. Приведите пример использования симметричной (несимметричной) нагрузки, соединенной звездой в технике.
11. Соберите схему лабораторной установки.
12. Расскажите порядок выполнения лабораторной работы.
Лабораторная работа № 6
Соединение приемника треугольником в трехфазной цепи
| |
| | | | | | | |
| | | | |
|
| 5. Создать обрыв линейного провода фазы А при установленной несимметричной нагрузке и включенном нулевом проводе путем размыкания рубильника Р1 и вновь провести те же наблюдения.
6. Восстановить целостность линейного провода А-А путем включения рубильнике P1. Оборвать нулевой провод, разомкнув рубильник Р2. Как и в предыдущем случае, нагрузка останется несимметричной.
Полученные экспериментальные данные необходимо обработать в следующем порядке:
а) найти отношение среднеарифметических значении линейных и фазных напряжений для опыта с симметричной нагрузкой и полученную величину сравнить с теоретическим значением;
б) рассчитать величины активной нагрузки каждой фазы для всех опытов по формуле:
 (6)
Результаты занести в таблицу.
Результаты измерений и расчетов (6)
Результаты занести в таблицу.
Результаты измерений и расчетов
| Данные измерений
| Результаты вычислений
| | Ток, мА
| Напряжение, В
| Нагрузка, Ом
| Активная мощность
| | фазные
| линейные
| Фазная
| Об-щая
| | IA
| IB
| IC
| IN
| UA
| UB
| UC
| UAB
| UBC
| UCA
| RA
| RB
| RC
| PA
| PB
| PC
| P
| | | | | | | | | | | | | | | | | | |
Примечание. Опыт №1 – симметричная активная нагрузка с нулевым проводом; №2 - несимметричная активная нагрузка с ну левым проводом; №3 - несимметричная активная нагрузка при обрыве линейного провода фазы А и наличии нулевого провода; №4 – несимметричная активная нагрузка без нулевого провода.
в) рассчитать активную мощность приемников каждой фазы для всех опытов по формуле:
  (7) (7)
и общую активную мощность соединения
 (8) (8)
| | |
Порядок выполнения работы
1. Собрать схему лабораторной установки, показанной на рис. 2
 Рис.2. Схема лабораторной установки
2. При отключенных потребителях (холостой ход линии) измерить напряжение на входе U1 и выходе U2 линии.
3. Тумблером подключить первый потребитель (резистор) и измерить U1, U2, I
4. Подключая последовательно остальные пять резисторов, повторить измерения U1, U2, I и все полученные результаты занести в таблицу.
Результаты измерений и расчетов
Рис.2. Схема лабораторной установки
2. При отключенных потребителях (холостой ход линии) измерить напряжение на входе U1 и выходе U2 линии.
3. Тумблером подключить первый потребитель (резистор) и измерить U1, U2, I
4. Подключая последовательно остальные пять резисторов, повторить измерения U1, U2, I и все полученные результаты занести в таблицу.
Результаты измерений и расчетов
| № п/п
| Измерено
| Вычислено
| | U1
| U2
| I
| ΔU
| RЛ
| P1
| P2
| P
| h
| RН
| | В
| В
| мА
| В
| Ом
| Вт
| Вт
| Вт
| %
| Ом
|
5. Вычислить потерю напряжения ΔU (формула 1), сопротивление проводов линии RЛ (2), мощность в начале линии Р1 (6) и P2 отдаваемую ЛЭП потребителям (7), потери мощности в проводах линии ΔР (4), коэффициент полезного действия работающей линии (8), величину эквивалентного сопротивления потребителей

6. Полученные результата занести в таблицу и построить в масштабе графические зависимости: ΔU= f( I); ΔP= f( I); U2= f( I); h= f( I).
7. По результатам работы сделать выводы и записать их в отчет.
Контрольные вопросы и задания.
1. Нарисуйте схему передачи электроэнергии от генератора электростанции до потребителя.
2. Каким напряжением выгодно передавать заданную мощность (высоким или низким) и почему?
| |
| | | | | | | |
| | | | |
|
| 3. Что такое потеря напряжения в линии? Как её можно определить?
4. 0т чего зависит потеря мощности в ЛЭП
5. Что такое коэффициент полезного действия линии и как он определяется?
6. Как найти сопротивление линии электропередачи?
7. Какие отклонения напряжения на зажимах электроприемников допускаются ГОСТом?
8. Расскажите о цели, порядке выполнения лабораторной работа.
9. Соберите схему лабораторной установки.
Лабораторная работа № 3
Последовательное соединение резистора, катушки индуктивности и конденсатора
Цель работы:
1) проверить основные соотношения для цепи, содержащей последовательно соединенные активные и реактивные элементы;
2) ознакомиться с построением векторных диаграмм напряжений и токов, а также треугольников сопротивлений и мощностей.
Основные теоретические положения
В данной работе рассматривается цепь синусоидального тока, состоящая из последовательно соединенных резисторов R, катушки индуктивности L и конденсатора C (рис. 1.).
 Рис.1. Последовательное соединение R, L, C
Напряжения на элементах при токе
Рис.1. Последовательное соединение R, L, C
Напряжения на элементах при токе  являются синусоидальными функциями времени: являются синусоидальными функциями времени:  , ,
 , ,  . .
| | |  Рис. 3. Векторные диаграммы токов и напряжений при несимметричной активной нагрузке фаз и обрыве нейтрального (а) и линейного (б) проводов
Обрыв, например, одного "из линейных проводов А-А" или перегорание предохранителя не нем (рис. 1) при целом нейтральном проводе приводит к отключению питания потребителей только фазы А. Режим работы двух других фаз не изменяется. Однако ток в нейтральном проводе IN несколько увеличится и станет равным векторной сумме только двух фазных токов IВ и IС (рис. 3 б). Обрыв в рассматриваемом случае еще и нейтрального провода может резко сказаться на работе включенных потребителей, так как произойдет перераспределение напряжений потребителей пропорционально величинам их сопротивлений.
При коротком замыкании в одной из фаз происходит плавление предохранителя в линейном проводе этой фазы (рис.1) и трехфазная цепь автоматически переходит в рассмотренный выше режим работы с обрывом линейного провода и целым нейтральным (рис.3 б).
Исходя из вышесказанного, всегда стремятся поддерживать целостность нейтрального провода, в него никогда не ставят предохранители или выключатели.
Порядок выполнения работы
1. Собрать схему (рис.4)
2. Замкнуть рубильники Р1 и P2 и после проверки преподавателем правильности соединений в схеме включить питание.
3. Изменяя выключателями число параллельно включенных резисторов в каждом фазной приемнике добиться симметричной активной нагрузки фаз, при которой амперметры фазных токов дают одинаковые показания. Амперметр, включенный в нулевой провод, должен показать отсутствие тока. Вольтметром со щупами измерить последовательно линейные UAB, UBC, UCA и фазные UA, UB, UC напряжения. Показания всех приборов записать в таблицу.
4. Создать несимметричную активную нагрузку по фазам, измерить фазные и линейные токи и напряжения. Обратить внимание на показания амперметра в нулевом проводе. Показания записать в таблицу. Рис. 3. Векторные диаграммы токов и напряжений при несимметричной активной нагрузке фаз и обрыве нейтрального (а) и линейного (б) проводов
Обрыв, например, одного "из линейных проводов А-А" или перегорание предохранителя не нем (рис. 1) при целом нейтральном проводе приводит к отключению питания потребителей только фазы А. Режим работы двух других фаз не изменяется. Однако ток в нейтральном проводе IN несколько увеличится и станет равным векторной сумме только двух фазных токов IВ и IС (рис. 3 б). Обрыв в рассматриваемом случае еще и нейтрального провода может резко сказаться на работе включенных потребителей, так как произойдет перераспределение напряжений потребителей пропорционально величинам их сопротивлений.
При коротком замыкании в одной из фаз происходит плавление предохранителя в линейном проводе этой фазы (рис.1) и трехфазная цепь автоматически переходит в рассмотренный выше режим работы с обрывом линейного провода и целым нейтральным (рис.3 б).
Исходя из вышесказанного, всегда стремятся поддерживать целостность нейтрального провода, в него никогда не ставят предохранители или выключатели.
Порядок выполнения работы
1. Собрать схему (рис.4)
2. Замкнуть рубильники Р1 и P2 и после проверки преподавателем правильности соединений в схеме включить питание.
3. Изменяя выключателями число параллельно включенных резисторов в каждом фазной приемнике добиться симметричной активной нагрузки фаз, при которой амперметры фазных токов дают одинаковые показания. Амперметр, включенный в нулевой провод, должен показать отсутствие тока. Вольтметром со щупами измерить последовательно линейные UAB, UBC, UCA и фазные UA, UB, UC напряжения. Показания всех приборов записать в таблицу.
4. Создать несимметричную активную нагрузку по фазам, измерить фазные и линейные токи и напряжения. Обратить внимание на показания амперметра в нулевом проводе. Показания записать в таблицу.
| |
| | | | | | | |
| | | | |
|
|  Рис. 2. Векторные диаграммы токов и напряжений: при симметричной (а) и несимметричной (б) активной нагрузке фаз
При несимметричной нагрузке фаз нарушается равенство фазных токов IА, IВ, IС и появляется ток IN, в нейтральном проводе (рис. 2 б).
Следует отметить, что при симметричной и несимметричной активной нагрузке фаз (рис. 2 а, б) наличие целого нейтрального провода обеспечивало постоянство фазных и линейных напряжений. Причем между этими напряжениями существует следующая зависимость: Рис. 2. Векторные диаграммы токов и напряжений: при симметричной (а) и несимметричной (б) активной нагрузке фаз
При несимметричной нагрузке фаз нарушается равенство фазных токов IА, IВ, IС и появляется ток IN, в нейтральном проводе (рис. 2 б).
Следует отметить, что при симметричной и несимметричной активной нагрузке фаз (рис. 2 а, б) наличие целого нейтрального провода обеспечивало постоянство фазных и линейных напряжений. Причем между этими напряжениями существует следующая зависимость:
 , (5)
которая легко может быть установлена из векторных диаграмм.
При несимметричной активной нагрузке и обрыве нейтрального провода фазные токи изменяются таким образом, чтобы их векторная сумма (2) стала разной нулю. Это приводит к смещению потенциала нейтральной точки и к нарушению равенстве между фазными напряжениями - фаза с большим сопротивлением оказывается под повышенным напряжением, что может привести к аварийной ситуации. Векторную диаграмму в этом случае строят по опытным данным методом засечек (рис. 3 а). Сначала вычерчивают треугольник линейных напряжений UAB, UBC, UCA, которые сохранили свое равенство. Затем из соответствующих вершин треугольника радиусами, равными измеренным фазным напряжениям UA, UC, UC, описывают дуги, пересечение которых определяет положение нейтральной точки. , (5)
которая легко может быть установлена из векторных диаграмм.
При несимметричной активной нагрузке и обрыве нейтрального провода фазные токи изменяются таким образом, чтобы их векторная сумма (2) стала разной нулю. Это приводит к смещению потенциала нейтральной точки и к нарушению равенстве между фазными напряжениями - фаза с большим сопротивлением оказывается под повышенным напряжением, что может привести к аварийной ситуации. Векторную диаграмму в этом случае строят по опытным данным методом засечек (рис. 3 а). Сначала вычерчивают треугольник линейных напряжений UAB, UBC, UCA, которые сохранили свое равенство. Затем из соответствующих вершин треугольника радиусами, равными измеренным фазным напряжениям UA, UC, UC, описывают дуги, пересечение которых определяет положение нейтральной точки.
| | | Согласно 2-му закону Кирхгофа для вектора напряжения на входе такой цепи может быть записано выражение
 ,
где ,
где  - соответственно активная, индуктивная и емкостная составляющая вектора напряжения на входе цепи.
Из этого выражения следует, что при известных - соответственно активная, индуктивная и емкостная составляющая вектора напряжения на входе цепи.
Из этого выражения следует, что при известных  , вектор , вектор  может быть получен построением векторной диаграммы. Свойства рассматриваемой цепи, а, следовательно, и вид векторной диаграммы, будет зависеть от соотношений между индуктивным и емкостным сопротивлениями может быть получен построением векторной диаграммы. Свойства рассматриваемой цепи, а, следовательно, и вид векторной диаграммы, будет зависеть от соотношений между индуктивным и емкостным сопротивлениями
 ; ;  ,
где ω – угловая частота;
f – частота питающей сети, Гц (f=50Гц);
L – индуктивность катушки, Гн;
C – емкость конденсатора, Ф;
На рис. 2, а показана векторная диаграмма для случая UL> UC, (xL > xC). Построение этой диаграммы начинают, откладывая в произвольном направлении вектор тока ,
где ω – угловая частота;
f – частота питающей сети, Гц (f=50Гц);
L – индуктивность катушки, Гн;
C – емкость конденсатора, Ф;
На рис. 2, а показана векторная диаграмма для случая UL> UC, (xL > xC). Построение этой диаграммы начинают, откладывая в произвольном направлении вектор тока  . Затем из точки О откладывают вектор . Затем из точки О откладывают вектор  , совпадающий по фазе с , совпадающий по фазе с  , вектор , вектор  , опережающий вектор тока на , опережающий вектор тока на  , и вектор , и вектор  , отстающий от , отстающий от  на угол на угол  . Для получения вектора напряжения . Для получения вектора напряжения  необходимо вначале сложить векторы необходимо вначале сложить векторы  и и  , определив тем самым вектор реактивного напряжения , определив тем самым вектор реактивного напряжения
 Складывая векторно
Складывая векторно  и и  , можно получить вектор напряжения на входе цепи , можно получить вектор напряжения на входе цепи  .
Угол сдвига фаз φ между напряжением .
Угол сдвига фаз φ между напряжением  , приложенным к зажимам цепи, и током , приложенным к зажимам цепи, и током  будет в этом случае положительным (напряжение опережает ток по фазе). будет в этом случае положительным (напряжение опережает ток по фазе).
| |
| | | | | | | |
| | | | |
|
|  Рис. 2. Векторная диаграмма (а), треугольники сопротивлений (б) и мощностей (в) для случая
Прямоугольный треугольник OAB называют треугольником напряжений.
Если модули напряжений, входящие в этот треугольник, разделить на модуль тока, то получим значения активного R, реактивного X и полного Z сопротивлений: Рис. 2. Векторная диаграмма (а), треугольники сопротивлений (б) и мощностей (в) для случая
Прямоугольный треугольник OAB называют треугольником напряжений.
Если модули напряжений, входящие в этот треугольник, разделить на модуль тока, то получим значения активного R, реактивного X и полного Z сопротивлений:
 ; ;  ; ;  , (2)
используя которые можно в определенном масштабе построить треугольник сопротивлений (рис 2, б). Из рассмотрения этого треугольника следует, что , (2)
используя которые можно в определенном масштабе построить треугольник сопротивлений (рис 2, б). Из рассмотрения этого треугольника следует, что
 Для получения треугольника мощностей (рис. 2, в) умножив модули напряжений
Для получения треугольника мощностей (рис. 2, в) умножив модули напряжений  , ,  и и  на модуль тока I: на модуль тока I:
 ; ;  ; ;  .
Где S – полная мощность цепи;
P – активная мощность цепи;
Q – реактивная мощность, равная Q= QL- QC.
Выражая значения Ua и UP через U (из прямоугольного треугольника САВ), будем иметь .
Где S – полная мощность цепи;
P – активная мощность цепи;
Q – реактивная мощность, равная Q= QL- QC.
Выражая значения Ua и UP через U (из прямоугольного треугольника САВ), будем иметь
 ; ;  , ,  , ,
 (3)
Хотя все три мощности имеют одну и туже размерность – "Вольт-Ампер", для их различия введены следующие наименования этой единицы измерения:
а) для P – "Ватт" (Вт);
б) для Q – "Вольт-Ампер-реактивный" (вар);
в) для S – "Вольт-Ампер" (ВА).
При рассмотрении случая, когда XL< XC, необходимо иметь в виду, что порядок построения векторной диаграммы аналогичен рассмотренному выше. Однако, т.к. UL< UC, угол φ принимает отрицательные значения (напряжение отстает по фазе от (3)
Хотя все три мощности имеют одну и туже размерность – "Вольт-Ампер", для их различия введены следующие наименования этой единицы измерения:
а) для P – "Ватт" (Вт);
б) для Q – "Вольт-Ампер-реактивный" (вар);
в) для S – "Вольт-Ампер" (ВА).
При рассмотрении случая, когда XL< XC, необходимо иметь в виду, что порядок построения векторной диаграммы аналогичен рассмотренному выше. Однако, т.к. UL< UC, угол φ принимает отрицательные значения (напряжение отстает по фазе от  ). ).
| | |   . (2)
Напряжение между началом я концом каждого потребителя, или между линейным и нейтральным проводом называется фазным напряжением (UФ) и обозначается соответственно: UA, UB, UC. Напряжение между началами двух потребителей или между двумя линейными проводами называется линейным напряжением (UЛ) и обозначается соответственно UAB, UBC, UCA.
В общем случае фазные и линейные напряжения связаны между собой согласно 2-му закону Кирхгофа: . (2)
Напряжение между началом я концом каждого потребителя, или между линейным и нейтральным проводом называется фазным напряжением (UФ) и обозначается соответственно: UA, UB, UC. Напряжение между началами двух потребителей или между двумя линейными проводами называется линейным напряжением (UЛ) и обозначается соответственно UAB, UBC, UCA.
В общем случае фазные и линейные напряжения связаны между собой согласно 2-му закону Кирхгофа:
 ; ;  ; ;  . (3)
Каждый из однофазных потребителей в трехфазной цепи характеризуется величинами полного сопротивления ZA, ZB, ZC и коэффициентами мощности cos φA, cos φВ, cos φС. При численном равенстве полных сопротивлений фазных нагрузок и равенстве их коэффициентов мощности имеет место симметричная нагрузка фаз. Нарушение хотя бы одного из отмеченных равенств создает несимметричную нагрузку.
Для потребителя каждой фазы справедливы, в общем случае, следующие зависимости: . (3)
Каждый из однофазных потребителей в трехфазной цепи характеризуется величинами полного сопротивления ZA, ZB, ZC и коэффициентами мощности cos φA, cos φВ, cos φС. При численном равенстве полных сопротивлений фазных нагрузок и равенстве их коэффициентов мощности имеет место симметричная нагрузка фаз. Нарушение хотя бы одного из отмеченных равенств создает несимметричную нагрузку.
Для потребителя каждой фазы справедливы, в общем случае, следующие зависимости:
 , ,  , ,  . (4)
В случае симметричной активной нагрузки фазные токи IА, IВ, IС равны друг другу по величине и на векторной диаграмме совпадают по направлению с соответствующими фазными напряжениями UAB, UBC, UCA (рис. 2, а): Тока в нейтральной проводе IN в этом случае не будет, что может быть подтверждено графическим решением векторного уравнения (2). . (4)
В случае симметричной активной нагрузки фазные токи IА, IВ, IС равны друг другу по величине и на векторной диаграмме совпадают по направлению с соответствующими фазными напряжениями UAB, UBC, UCA (рис. 2, а): Тока в нейтральной проводе IN в этом случае не будет, что может быть подтверждено графическим решением векторного уравнения (2).
| |
| | | | | | | |
| | | | |
|
|
Лабораторная работа № 5
Соединение приемников звездой трехфазной цепи
Цель работы:
1. Установить соотношение между линейными и фазными величинами токов и напряжений при различных режимах работы соединения;
2. По опытным данным построить векторные диаграммы напряжений и токов при симметричной нагрузке фаз;
3. Выяснить влияние обрыва линейного и нейирального проводов на режим работы потребителей.
Основные теоретические положения
В современной электроэнергетике наибольшее распространение получили трехфазные цепи, которые были разработаны в конце XIX века выдающимся русским электротехником Михаилом Осиповичем Доливо-Добровольским.
Источником электрической энергии в трехфазных цепях является синхронный генератор, у которого три обмотки A, B, C (фазы) сдвинуты одна по отношению к другой на угол 1200. От такого генератора могут отходить четыре провода – три линейных A, B, C и один нейтральный N. К этим проводам присоединяются потребители (приемники), которые могут быть как однофазными (лампы накаливания, бытовые электроприборы, ручной электроинструмент и т.д.), так и трехфазными (асинхронные двигатели, индукционные печи и т.д.).
Отдельные фазы трехфазных потребителей или однофазные потребители при подключении в трехфазную цепь могут соединяться между собой по способу "звезда". Для соединения звездой, например, трех однофазных потребителей необходимо их концы X, Y, Z объединить электрически в одну общую (нейтральную) точку N. К полученной нейтральной точке присоединяется нейтральный провод N- N., а к началам потребителей A, B, C – соответственно линейные провода A-А, B-В, C-С от генератора (рис.1, а).
Рисунок 1
Для соединения звезда характерно, что токи в линейных проводах IЛ являются одновременно и фазными токами IФ подключенных к этим проводам потребителей:
 (1)
При установлении соотношения по 1-му закону Кирхгофа между фазными токами потребителей IА, IВ, IС током в нейтральном проводе IN принято, что фазные токи всегда условно направлены к нейтральной точке соединения N, а ток в нейтральном проводе - от этой точки (рис.1, б): (1)
При установлении соотношения по 1-му закону Кирхгофа между фазными токами потребителей IА, IВ, IС током в нейтральном проводе IN принято, что фазные токи всегда условно направлены к нейтральной точке соединения N, а ток в нейтральном проводе - от этой точки (рис.1, б):
| | | Реактивное индуктивное и емкостное сопротивления цепи переменного тока могут также полностью уравновесить друг друга XL- XC=0. В этом случае в цепи возникает резонанс напряжений, т.е. явление, при котором в последовательной цепи, состоящей из элементов R, L, и C, общее напряжение на входе совпадает по фазе с ее током. При этом индуктивное и емкостное напряжения компенсируют друг друга UL+ UC=0, т.к. они равны по величине и противоположны по фазе. Отметим, что каждая из реактивных составляющих  , т.е. , т.е.  и и  , может быть значительно больше, чем напряжение, приложенное к цепи.
Порядок построения векторной диаграммы сохраняется прежним. Согласно условию возникновения резонанса напряжений , может быть значительно больше, чем напряжение, приложенное к цепи.
Порядок построения векторной диаграммы сохраняется прежним. Согласно условию возникновения резонанса напряжений
  ,
этот режим может быть получен при изменении частоты питающего напряжения, величины индуктивности или емкости соответствующих элементов рассматриваемой цепи.
Порядок выполнения работы
1. Собрать схему в соответствии с рис.3 и после проверки ее преподавателем замкнуть рубильник на стенде. ,
этот режим может быть получен при изменении частоты питающего напряжения, величины индуктивности или емкости соответствующих элементов рассматриваемой цепи.
Порядок выполнения работы
1. Собрать схему в соответствии с рис.3 и после проверки ее преподавателем замкнуть рубильник на стенде.
 Рис. 3. Электрическая схема лабораторной установки
2. Измерить действующие значения тока в цепи, а также напряжений на входе цепи, на резисторе UR10, катушке индуктивности UK, батарее конденсаторов UC при замкнутых тумблерах: а) P1; б) P1 и P2; в) P1, P2 и P3. Полученные данные занести в табл.1.
Результаты измерений Таблица 1. Рис. 3. Электрическая схема лабораторной установки
2. Измерить действующие значения тока в цепи, а также напряжений на входе цепи, на резисторе UR10, катушке индуктивности UK, батарее конденсаторов UC при замкнутых тумблерах: а) P1; б) P1 и P2; в) P1, P2 и P3. Полученные данные занести в табл.1.
Результаты измерений Таблица 1.
| Значение C
| I
| U
| UR10
| UK
| UC
| | мА
| В
| В
| В
| В
| | С=С1
С=С1+С2
С=С1+С2+С3
|
|
|
|
|
| При исследовании процессов в цепях переменного тока следует учитывать, что всякая катушка индуктивности обладает определенным | |
| | | | | | | |
| | | | |
|
| 3.активным сопротивлением RK, которое можно рассматривать как включенное последовательно с индуктивностью (рис. 4).
 Рис. 4. Расчетная схема замещения
Поэтом для получения достоверных результатов необходимо выделить активную и индуктивную составляющие напряжений на катушке
Рис. 4. Расчетная схема замещения
Поэтом для получения достоверных результатов необходимо выделить активную и индуктивную составляющие напряжений на катушке
 ; ;  .
Активная составляющая напряжения цепи находится после этого суммированием напряжения, измеренного на резисторе R10 и и напряжения URK, полученного расчетных путем: .
Активная составляющая напряжения цепи находится после этого суммированием напряжения, измеренного на резисторе R10 и и напряжения URK, полученного расчетных путем:
 .
Значение UP находится из соотношения UP= UL- UC.
4. полученные данные занести в табл.2 и по ним построить векторные диаграммы для трех случаев.
Результаты расчетов Таблица 2 .
Значение UP находится из соотношения UP= UL- UC.
4. полученные данные занести в табл.2 и по ним построить векторные диаграммы для трех случаев.
Результаты расчетов Таблица 2
| Значение C
| URK
| UL
| Ua
| UP
| R
| XC
| X
| Z
| cosφ
| sinφ
| S
| P
| Q
| | В
| В
| В
| В
| Ом
| Ом
| Ом
| Ом
| -
| -
| ВА
| Вт
| вар
| | C=C1
C=C1+C2
C=C1+C2+C3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Используя выражение (2) и соотношение  , определить R, XC, X1, Z, найти , определить R, XC, X1, Z, найти  и и  . .
6. С помощью соотношения (3) найти P, S, и Q.
7. По полученным данным построить теругольники мощностей и сопротивлений.
8. Сделать выводы об основных соотношениях в цепи переменного тока, содержащей последовательно соединенные R, L, C, о возможных режимах работы.
| | | в) активную мощность потребителя или цепи:  , Вт (1-й и 3-й опыты) и , Вт (1-й и 3-й опыты) и  , Вт (2-й опыт);
г) реактивную индуктивную мощность цепи: , Вт (2-й опыт);
г) реактивную индуктивную мощность цепи:  , вар;
д) реактивную емкостную мощность конденсатора: , вар;
д) реактивную емкостную мощность конденсатора:  , вар (3-й опыт);
е) суммарную реактивную мощность, потребляемую из сети (от генератора): Q= QL- QC,
ж) полную электрическую млщность потребителя: , вар (3-й опыт);
е) суммарную реактивную мощность, потребляемую из сети (от генератора): Q= QL- QC,
ж) полную электрическую млщность потребителя:  , ВА;
з) коэффициент мощности цепи переменного тока: , ВА;
з) коэффициент мощности цепи переменного тока:  ;
к) общий ток цепи: ;
к) общий ток цепи:  .
7. Для каждого опыта вычислений построить в масштабе треугольники мощностей.
8. По полученным результатам лабораторной работы сделать выводы о роли и значении коэффициента мощности в электрических цепях, необходимости и способах его повышения.
Контрольные вопросы и задания
1. Что называется коэффициентом мощности электрической цепи?
2. Поясните природу угла сдвига по фазе φ между током и напряжением в электрической цепи.
3. Как можно рассчитать величину cosφ цепи?
4. Для расчета какой мощности цепи используется значение cosφ?
5. Влияет ли величина cosφ на значение тока при неизменных напряжении и активной мощности в цепи?
6. В чем заключается технико-экономическое значение повышения cosφ?
7. Какие естественные способы повышения cosφ Вы знаете?
8. Поясните суть и методы искусственных способов повышения cosφ.
9. Влияет ли и почему значение cosφ на нагрев проводов линии электропередач?
10. Расскажите о цели и порядке проведения работы.
11. Соберите схему лабораторной установки. .
7. Для каждого опыта вычислений построить в масштабе треугольники мощностей.
8. По полученным результатам лабораторной работы сделать выводы о роли и значении коэффициента мощности в электрических цепях, необходимости и способах его повышения.
Контрольные вопросы и задания
1. Что называется коэффициентом мощности электрической цепи?
2. Поясните природу угла сдвига по фазе φ между током и напряжением в электрической цепи.
3. Как можно рассчитать величину cosφ цепи?
4. Для расчета какой мощности цепи используется значение cosφ?
5. Влияет ли величина cosφ на значение тока при неизменных напряжении и активной мощности в цепи?
6. В чем заключается технико-экономическое значение повышения cosφ?
7. Какие естественные способы повышения cosφ Вы знаете?
8. Поясните суть и методы искусственных способов повышения cosφ.
9. Влияет ли и почему значение cosφ на нагрев проводов линии электропередач?
10. Расскажите о цели и порядке проведения работы.
11. Соберите схему лабораторной установки.
| |
| | | | | | | |
| | | | |
|
|  Рис. 2. Электрическая схема лабораторной установки
2. Определить коэффициент мощности цепи, содержащей обмотку возбуждения однофазного асинхронного двигателя с активным сопротивлением R и индуктивностью L. Для этого разомкнуть тумблер P1 и P2, а затем включить стенд. Снять показания приборов и записать их в таблицу измерений и расчетов.
3. Исследовать способ повышения cosφ цепи с обмоткой возбуждения при параллельном подключении к ней электрической печи с резистивным нагревательным элементом, имеющем сопротивление Rдоб. Для этого замкнуть тумблер P1, снять показания приборов и записать их в таблицу.
4. Исследовать способ повышения cosφ цепи с обмоткой возбуждения при параллельном подключении к ней статического конденсатора, имеющего реактивное емкостное сопротивление XC. Для этого разомкнуть тумблер P1 и замкнуть тумблер P2. Снять показания приборов и записать их в таблицу.
5. Отключить стенд и показать результаты наблюдений преподавателю.
Результаты измерений и расчетов Таблица 5
Рис. 2. Электрическая схема лабораторной установки
2. Определить коэффициент мощности цепи, содержащей обмотку возбуждения однофазного асинхронного двигателя с активным сопротивлением R и индуктивностью L. Для этого разомкнуть тумблер P1 и P2, а затем включить стенд. Снять показания приборов и записать их в таблицу измерений и расчетов.
3. Исследовать способ повышения cosφ цепи с обмоткой возбуждения при параллельном подключении к ней электрической печи с резистивным нагревательным элементом, имеющем сопротивление Rдоб. Для этого замкнуть тумблер P1, снять показания приборов и записать их в таблицу.
4. Исследовать способ повышения cosφ цепи с обмоткой возбуждения при параллельном подключении к ней статического конденсатора, имеющего реактивное емкостное сопротивление XC. Для этого разомкнуть тумблер P1 и замкнуть тумблер P2. Снять показания приборов и записать их в таблицу.
5. Отключить стенд и показать результаты наблюдений преподавателю.
Результаты измерений и расчетов Таблица 5
| № п/п
| Измерено
| Вычислено
| | U
| I1
| I2
| XL
| XC
| P
| QL
| QC
| Q
| S
| cosφ
| I
| | В
| мА
| мА
| Ом
| Ом
| Вт
| вар
| вар
| вар
| ВА
| -
| мА
| 6. Пользуясь результатами наблюдений и значениями параметров схемы R, L, и Rдоб вычислить для опытов и записать в таблицу:
а) индуктивное сопротивление обмотки возбуждения:
 , Ом; , Ом;
б) реактивное емкостное сопротивление конденсатора:
 , Ом; , Ом;
| | | Контрольные вопросы и задания
1. Какое соединение элементов электрической цепи называется последовательным?
2. Чему равен сдвиг по фазе между напряжением и током при включении в цепь сопротивлений: активного, индуктивного, емкостного?
3. Как определяется полное сопротивление цепи при последовательном соединении R, L, C.
4. Напишите 2-й закон Кирхгофа для цепи с R, L, C.
5. Начертите векторную диаграмму напряжений для цепи с последовательно соединенными R, L, C при условии
а) XL> XC б) XL< XC
6. Постройте треугольники сопротивлений и мощностей для случаев, указанных в п.5.
7. Напишите формулу для определения активной, реактивной и полной мощности. В каких единицах измеряются P, S и Q?
8. Как зависят от частоты питающей сети индуктивное и емкостное сопротивления?
9. Расскажите о резонансе напряжений. Постройте векторную диаграмму.
10. Расскажите о порядке выполнения лабораторной работы.
11. Соберите схему лабораторной установки.
Лабораторная работа № 4
Цель работы:
1) ознакомить с понятием и технико- экономическим значением повышения коэффициента мощности;
2) изучить практические способы определения и улучшения коэффициента мощности электрических цепей.
Основные теоретические положения
Источником электрической энергии или электрической мощности в цепи переменного тока являются специальные электрические машины - генераторы. В паспорте генератора указываются номинальные значения: тока I и напряжения U, которые от него можно получить и которыми однозначно определяется вырабатываемая им номинальная или полная электрическая мощности,
 (1)
Эта мощность (1) передается по линии электропередач (ЛЭП) к потребителям большинство из которых имеет в своих конструкциях обмотки различного типа и вследствие этого обладают активно-индуктивным электрическим сопротивлением (электродвигатели, сварочные и силовые трансформаторы, электрические печи, установки электрического освещения, электромагниты различного (1)
Эта мощность (1) передается по линии электропередач (ЛЭП) к потребителям большинство из которых имеет в своих конструкциях обмотки различного типа и вследствие этого обладают активно-индуктивным электрическим сопротивлением (электродвигатели, сварочные и силовые трансформаторы, электрические печи, установки электрического освещения, электромагниты различного | |
| | | | | | | |
| | | | |
|
| назначения и т.д.). Поэтому подводимые от генератора ток I и напряжение U сдвинута по фазе у потребителя и во всей цепи на некоторый угол φ ,a величина активной мощности определяется:
 (2)
Таким образом, только часть электрической мощности, вырабатываемой генератором и подводимой к потребителю, необратимо преобразуется в поленую активную мощность потребителя Р: механическую, тепловую, световую и т.д. Степень полезного использования потребителем электрической мощности генератора и определяется величиной косинуса. угла сдвига фаз между током I и напряжением U: (2)
Таким образом, только часть электрической мощности, вырабатываемой генератором и подводимой к потребителю, необратимо преобразуется в поленую активную мощность потребителя Р: механическую, тепловую, световую и т.д. Степень полезного использования потребителем электрической мощности генератора и определяется величиной косинуса. угла сдвига фаз между током I и напряжением U:
 , (3)
Который часто называют коэффициентом мощности потребителя или коэффициентом мощности цепи переменного тока.
Процесс передачи электрической мощности от генератора к потребителю, имеющему активно-индуктивное сопротивление, характеризуется помимо активной мощности еще и реактивной мощностью: , (3)
Который часто называют коэффициентом мощности потребителя или коэффициентом мощности цепи переменного тока.
Процесс передачи электрической мощности от генератора к потребителю, имеющему активно-индуктивное сопротивление, характеризуется помимо активной мощности еще и реактивной мощностью:
 (4)
Реактивная мощность идет на создание индуктивными катушками потребителя переменных магнитных полей. Особенностью является, что этой мощностью непрерывно обмениваются между собой ЛЭП, генератор и потребитель.
Между рассмотренными мощностями S, P и Q существует зависимость: (4)
Реактивная мощность идет на создание индуктивными катушками потребителя переменных магнитных полей. Особенностью является, что этой мощностью непрерывно обмениваются между собой ЛЭП, генератор и потребитель.
Между рассмотренными мощностями S, P и Q существует зависимость:
 (5)
Очевидно, что генератор выгодно эксплуатировать так, чтобы вырабатываемая им электрическая энергия полностью использовалась у потребителя на совершение полезной, нужной людям работы. Такое использование мощности генератора происходит только тогда, когда коэффициент мощности потребителя равен единице (cosφ=1); (5)
Очевидно, что генератор выгодно эксплуатировать так, чтобы вырабатываемая им электрическая энергия полностью использовалась у потребителя на совершение полезной, нужной людям работы. Такое использование мощности генератора происходит только тогда, когда коэффициент мощности потребителя равен единице (cosφ=1);
 Всякое уменьшение cosφ, значение которого определяется соотношением активного и индуктивного сопротивлений у потребителя, приводит к неполному использованию мощности генератора в полезных целях, т.е. наряду с активной электрической мощностью для потребителя генератор должен вырабатывать еще и реактивную мощность. Кроме того, если потребитель рассчитан на неизменное напряжение и мощность P, то потребляемый им ток, который также является током, всей цепи и генератора, будет тем больше, чем меньше коэффициент мощности:
Всякое уменьшение cosφ, значение которого определяется соотношением активного и индуктивного сопротивлений у потребителя, приводит к неполному использованию мощности генератора в полезных целях, т.е. наряду с активной электрической мощностью для потребителя генератор должен вырабатывать еще и реактивную мощность. Кроме того, если потребитель рассчитан на неизменное напряжение и мощность P, то потребляемый им ток, который также является током, всей цепи и генератора, будет тем больше, чем меньше коэффициент мощности:
 . (6)
Таким образом, при низких значениях коэффициента мощности народному хозяйству наносится определенный технико-экономический ущерб, поскольку из-за повышенных значений тока (6) и загрузки цепи значительными потоками реактивной мощности: . (6)
Таким образом, при низких значениях коэффициента мощности народному хозяйству наносится определенный технико-экономический ущерб, поскольку из-за повышенных значений тока (6) и загрузки цепи значительными потоками реактивной мощности:
| | | - возникают дополнительные потери электроэнергии на нагрев проводов воздушных и кабельных линий генератора;
- появляются дополнительные потери напряжения в сетях, что ухудшает электроснабжение и работу потребителей;
- уменьшается пропускная способность линии электропередач, что требует повышенного расхода металла на увеличение площадей сечения проводов;
- снижается к.п.д. генератора и электрической цепи в целом.
Для устранения отмеченных недостатков стремятся повышать cosφ цепей до значения 0.5-0.96. Повышение коэффициента мощности, потребителей промышленных предприятий осуществляется прежде всего естественным путем, главным образом за счет упорядочения энергетического режима оборудования, рационального использования его мощностей, замены малозагруженных двигателей двигателями меньших мощностей, ограничения длительности режимов холостого хода трансформаторов и двигателей и т.д. В случае необходимости прибегают к искусственному повышению коэффициента мощности, когда параллельно к потребителю подключают еще одно устройство с активным сопротивлением или компенсирующие устройства с емкостным сопротивлением – статические конденсаторы или синхронные компенсаторы. В последнем случае потребитель будет получать реактивную мощность на образование магнитных полей полностью, или частично не от генератора по ЛЭП, а от рядом расположенного компенсирующего устройства. Графическая иллюстрация искусственных методов повышения cosφ может быть треугольниками мощностей (рис. 1.).
 Рисунок 1. Треугольники мощностей
а) для исходной цепи с активно-индуктивным сопротивлением;
б) при параллельном подключении к цепи активного сопротивления;
в) при параллельном подключении к цепи емкостного сопротивления.
Порядок выполнения работы
1. Собрать на стенде электрическую схему лабораторной работы (рис. 2) и дать ее проверить преподавателю. Рисунок 1. Треугольники мощностей
а) для исходной цепи с активно-индуктивным сопротивлением;
б) при параллельном подключении к цепи активного сопротивления;
в) при параллельном подключении к цепи емкостного сопротивления.
Порядок выполнения работы
1. Собрать на стенде электрическую схему лабораторной работы (рис. 2) и дать ее проверить преподавателю.
| |
Дата добавления: 2020-11-15; просмотров: 125; | Поделиться с друзьями:
|

Мы поможем в написании ваших работ!


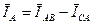 ;
;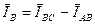 ; (1)
; (1)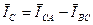 .
.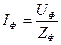 (2)
(2)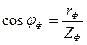 . (3)
. (3) ; (4)
; (4)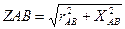 ; (5)
; (5) . (6)
. (6)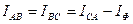 . (7)
. (7)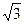 .
.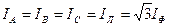 (8)
(8)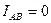 (9)
(9) (10)
(10)
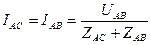 (11)
(11)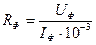 .
.

 .
При составлении уравнений по законам Кирхгофа необходимо предварительно задаться положительными направлениями токов и напряжений. При этом нужно учитывать, что в приемниках электрической энергии напряжение и ток направлены в одну сторону, а в источниках питания - в противоположную.
Согласно 1-му закону Кирхгофа, алгебраическая сумма токов, сходящихся в любом узле цепи, равна нулю, т.е.
.
При составлении уравнений по законам Кирхгофа необходимо предварительно задаться положительными направлениями токов и напряжений. При этом нужно учитывать, что в приемниках электрической энергии напряжение и ток направлены в одну сторону, а в источниках питания - в противоположную.
Согласно 1-му закону Кирхгофа, алгебраическая сумма токов, сходящихся в любом узле цепи, равна нулю, т.е.
 .
Со знаком "+" в это уравнение следует включать токи, направленные к узлу, а со знаком "-" – токи, отходящие от узла (допускается и наоборот).
С помощью этого закона может быть описано, например, электрическое состояние схемы, представляющее собой параллельное соединение элементов и показанное на рис. 1 а.
.
Со знаком "+" в это уравнение следует включать токи, направленные к узлу, а со знаком "-" – токи, отходящие от узла (допускается и наоборот).
С помощью этого закона может быть описано, например, электрическое состояние схемы, представляющее собой параллельное соединение элементов и показанное на рис. 1 а.
 или
или  .
.
 Рис. 1. Параллельное соединение элементов:
а – общая схема; б – включение нагревательного элемента (НЭ), двигателя (М) вентилятора и ламп накаливания (Л); в- включение амперметра с шунтом.
Так как при параллельном соединении все элементы находятся под одним и тем же напряжением, то, используя закон Ома, это уравнение можно записать в виде
Рис. 1. Параллельное соединение элементов:
а – общая схема; б – включение нагревательного элемента (НЭ), двигателя (М) вентилятора и ламп накаливания (Л); в- включение амперметра с шунтом.
Так как при параллельном соединении все элементы находятся под одним и тем же напряжением, то, используя закон Ома, это уравнение можно записать в виде
 ;
;  ;
;  ,
где RЭ и gЭ – эквивалентные сопротивление и проводимость данной цепи соответственно.
Благодаря тому, что параллельное соединение обеспечивает одинаковое напряжение на всех приемниках, оно нашло широкое распространение в практической электротехнике.
Так, например, параллельно включаются осветительные устройства, нагревательные элементы, радио- и телеаппаратура, холодильники и др. электроприемники в жилых домах (рис. 1 б).
Нередко такое соединение используется для расширения пределов измерения амперметров (рис. 1 в) и в других случаях.
По 2-му закону Кирхгофа алгебраическая сумма напряжений всех участков замкнутого контура равна нулю:
,
где RЭ и gЭ – эквивалентные сопротивление и проводимость данной цепи соответственно.
Благодаря тому, что параллельное соединение обеспечивает одинаковое напряжение на всех приемниках, оно нашло широкое распространение в практической электротехнике.
Так, например, параллельно включаются осветительные устройства, нагревательные элементы, радио- и телеаппаратура, холодильники и др. электроприемники в жилых домах (рис. 1 б).
Нередко такое соединение используется для расширения пределов измерения амперметров (рис. 1 в) и в других случаях.
По 2-му закону Кирхгофа алгебраическая сумма напряжений всех участков замкнутого контура равна нулю:
 или
или  .
При составлении уравнений по этому закону слагаемые берут со знаком "+", когда произвольно выбранное направление обхода контура совпадает с направлением U или I. В противном случае слагаемые берут со знаком "-". Например, для цепи, показанной на рис. 2 а
.
При составлении уравнений по этому закону слагаемые берут со знаком "+", когда произвольно выбранное направление обхода контура совпадает с направлением U или I. В противном случае слагаемые берут со знаком "-". Например, для цепи, показанной на рис. 2 а
 или
или  .
.
 .
. . (3)
Например, для фазного потребителя AB
. (3)
Например, для фазного потребителя AB
 ; (4)
; (4)
 ; (5)
; (5)
 . (6)
Очевидно, что для симметричной нагрузки фазные токи равны между собой:
. (6)
Очевидно, что для симметричной нагрузки фазные токи равны между собой:
 . (7)
Линейные токи также равны между собой и превышают фазные в
. (7)
Линейные токи также равны между собой и превышают фазные в  .
.
 (8)
Эта зависимость вытекает из построения векторной диаграммы токов и напряжении при симметричной активной нагрузке (рис. 1 б). В этом случае фазные токи совпадают по направлению с фазными напряжениями, линейные токи определяются графически решением системы уравнений (1).
Несимметричная нагрузка связана с неравенством фазных токов (по модулю и фазе) и нарушением соотношения (8).
При разрыве цепи потребителя АВ ток
(8)
Эта зависимость вытекает из построения векторной диаграммы токов и напряжении при симметричной активной нагрузке (рис. 1 б). В этом случае фазные токи совпадают по направлению с фазными напряжениями, линейные токи определяются графически решением системы уравнений (1).
Несимметричная нагрузка связана с неравенством фазных токов (по модулю и фазе) и нарушением соотношения (8).
При разрыве цепи потребителя АВ ток
 (9)
Потребители BC и СА остаются подключенными к линейным проводам под неизменным напряжением. Поэтому отключение потребителя АВ не повлияет на работу потребителей ВС и СА. Линейный ток IА станет равным фазному ICA, IB равным IBC. Линейный ток IC не изменится.
Обрыв линейного провода А окажет существенное влияние на режим работы соединения. В этом случае создаются две параллельные цепи, включенные под линейное напряжение – потребитель ВС и последовательное соединение потребителей ZAC, ZBC.
Фазный ток
(9)
Потребители BC и СА остаются подключенными к линейным проводам под неизменным напряжением. Поэтому отключение потребителя АВ не повлияет на работу потребителей ВС и СА. Линейный ток IА станет равным фазному ICA, IB равным IBC. Линейный ток IC не изменится.
Обрыв линейного провода А окажет существенное влияние на режим работы соединения. В этом случае создаются две параллельные цепи, включенные под линейное напряжение – потребитель ВС и последовательное соединение потребителей ZAC, ZBC.
Фазный ток
 (10)
не изменится, а ток во второй цепи
(10)
не изменится, а ток во второй цепи

 (11)
будет определяться суммой сопротивлений фазных нагрузок АС и АВ. Соответственно этому и распределение фазных напряжений UAC и UAB, будет зависеть от соотношения сопротивлений фазных потребителей АС и АВ. Поэтому такой режим работы соединения, нежелателен.
(11)
будет определяться суммой сопротивлений фазных нагрузок АС и АВ. Соответственно этому и распределение фазных напряжений UAC и UAB, будет зависеть от соотношения сопротивлений фазных потребителей АС и АВ. Поэтому такой режим работы соединения, нежелателен.
 Рис. 2. Последовательное соединение элементов:
а – общая схема; б – схема расширения пределов измерения; в – схема генератора постоянного тока
Так как при последовательном соединении по всем элементам протекает один и тот же ток, то, используя закон Ома, можно записать
Рис. 2. Последовательное соединение элементов:
а – общая схема; б – схема расширения пределов измерения; в – схема генератора постоянного тока
Так как при последовательном соединении по всем элементам протекает один и тот же ток, то, используя закон Ома, можно записать
 или
или  .
Приемники электрической энергии последовательно соединяются относительно редко, т.к. исключается возможность независимого их включения и отключения, а при выходе из строя одного из приемников отключаются и все остальные.
В качестве примера можно привести схему генератора постоянного тока последовательного возбуждения (рис. 2 в). В измерительной технике последовательным включением добавочных резисторов расширяют пределы измерения вольтметров (рис. 2 б) и т.п.
Сложным (смешанным) соединением называют электрические цепи, в состав которых входят последовательно и параллельно соединенные участки.
К такому соединению относится и схема лабораторной установки, показанной на рис. 3.
.
Приемники электрической энергии последовательно соединяются относительно редко, т.к. исключается возможность независимого их включения и отключения, а при выходе из строя одного из приемников отключаются и все остальные.
В качестве примера можно привести схему генератора постоянного тока последовательного возбуждения (рис. 2 в). В измерительной технике последовательным включением добавочных резисторов расширяют пределы измерения вольтметров (рис. 2 б) и т.п.
Сложным (смешанным) соединением называют электрические цепи, в состав которых входят последовательно и параллельно соединенные участки.
К такому соединению относится и схема лабораторной установки, показанной на рис. 3.
 Рис. 3. Схема лабораторной установки
Электрическое состояние этой схемы описывается следующими уравнениями
Рис. 3. Схема лабораторной установки
Электрическое состояние этой схемы описывается следующими уравнениями
 ;
;  .
Порядок выполнения работы
1. Собрать схему лабораторной установки (рис .3).
.
Порядок выполнения работы
1. Собрать схему лабораторной установки (рис .3).
 (1-й способ);
(1-й способ);  (2-й способ).
(2-й способ). Рис. 2
Фазные потребители защищены от токов короткого замыкания плавкими предохранителями (F UAB, FUBC, FUBC). Короткое, замыкание в фазе АВ, например, приведет к плавлению предохранителя F UAB,что эквивалентно разрыву фазной нагрузки АВ.
На линейных проводах также установлены предохранители F UA, F UA, F UC. Плавление любого из них создает отключение соответствующего линейного провода.
С учетом этого в лабораторной работе изучаются следующие режимы работы соединения "треугольник":
1. Симметричный режим нагрузки фаз.
2. Несимметричный режим.
3. Режим обрыва фазы АВ.
4. Режим обрыва линейного провода А.
При соединении "треугольник" фазный потребитель подключен к двум линейным проводам, т.е. находится под линейные напряжением, которое одновременно является и фазным. Поэтому UФ= UЛ (рис. 2).
При установлении соотношения между фазными и линейными токами принято условие, что линейные токи направлены в условно положительном направлении от источника электрической энергии к потребителю, а фазные токи – от начала к концу фазного потребителя.
Применив 1-й закон Кирхгофа для узлов А Z, ВХ, С Y, можно легко получить следующие векторные уравнения:
Рис. 2
Фазные потребители защищены от токов короткого замыкания плавкими предохранителями (F UAB, FUBC, FUBC). Короткое, замыкание в фазе АВ, например, приведет к плавлению предохранителя F UAB,что эквивалентно разрыву фазной нагрузки АВ.
На линейных проводах также установлены предохранители F UA, F UA, F UC. Плавление любого из них создает отключение соответствующего линейного провода.
С учетом этого в лабораторной работе изучаются следующие режимы работы соединения "треугольник":
1. Симметричный режим нагрузки фаз.
2. Несимметричный режим.
3. Режим обрыва фазы АВ.
4. Режим обрыва линейного провода А.
При соединении "треугольник" фазный потребитель подключен к двум линейным проводам, т.е. находится под линейные напряжением, которое одновременно является и фазным. Поэтому UФ= UЛ (рис. 2).
При установлении соотношения между фазными и линейными токами принято условие, что линейные токи направлены в условно положительном направлении от источника электрической энергии к потребителю, а фазные токи – от начала к концу фазного потребителя.
Применив 1-й закон Кирхгофа для узлов А Z, ВХ, С Y, можно легко получить следующие векторные уравнения:
 ;
;
 ; (1)
; (1)
 .
Каждый из фазных токов IАВ, IBC, ICA рассчитывается по модулю
.
Каждый из фазных токов IАВ, IBC, ICA рассчитывается по модулю
 (2)
и по фазе
(2)
и по фазе
 б
Рис. 1
Такое соединение более наглядно может быть показано в виде треугольника (рис. 1 б).
Каждый из однофазных потребителей определяется величинами полного сопротивления ZAB, ZBC, ZCA и коэффициента мощности cos φAB, cos φBC, cos φCA.
При равенстве полных сопротивлений фазных нагрузок и их коэффициентов мощности создается симметричная нагрузка соединения. Нарушения этих равенств создает несимметричную нагрузку.
б
Рис. 1
Такое соединение более наглядно может быть показано в виде треугольника (рис. 1 б).
Каждый из однофазных потребителей определяется величинами полного сопротивления ZAB, ZBC, ZCA и коэффициента мощности cos φAB, cos φBC, cos φCA.
При равенстве полных сопротивлений фазных нагрузок и их коэффициентов мощности создается симметричная нагрузка соединения. Нарушения этих равенств создает несимметричную нагрузку.
 Рис.1. Принципиальная схема производства, передачи и распределения электроэнергии:
1-трехфазный генератор электростанции; 2-трансформаторная подстанция (ТП) с повышающим трансформатором; 3-воздушная линия электроснабжения (ЛЭП); 4-главная понижающая подстанция; 5-ТП с поникающим трансформатором; 6-кабепьнае воздушные распределительные линии электроснабжения; 7-ТП3 и ТП4 - трансформаторные подстанции потребителей электроэнергии; 8-приемники электроэнергии.
В условиях предприятии стройиндустрии, как и вообще промышленных предприятий, а также в жилых районах и на стройплощадках, распределение электроэнергии осуществляется и кабельными линиями (КЛ), которые отличаются высокой надежностью электроснабжения. Они не подвержены влиянию ветра и гололеда, не загромождают, подобно ВЛ, улицы ropoда и территории предприятий
При передаче электроэнергии от электростанции к потребителю, т.е. при прохождении по проводам электрического тока, в ЛЭП возникает потеря напряжения, под которой понимают разность напряжений в начале U1 и в конце U2 линии:
Рис.1. Принципиальная схема производства, передачи и распределения электроэнергии:
1-трехфазный генератор электростанции; 2-трансформаторная подстанция (ТП) с повышающим трансформатором; 3-воздушная линия электроснабжения (ЛЭП); 4-главная понижающая подстанция; 5-ТП с поникающим трансформатором; 6-кабепьнае воздушные распределительные линии электроснабжения; 7-ТП3 и ТП4 - трансформаторные подстанции потребителей электроэнергии; 8-приемники электроэнергии.
В условиях предприятии стройиндустрии, как и вообще промышленных предприятий, а также в жилых районах и на стройплощадках, распределение электроэнергии осуществляется и кабельными линиями (КЛ), которые отличаются высокой надежностью электроснабжения. Они не подвержены влиянию ветра и гололеда, не загромождают, подобно ВЛ, улицы ropoда и территории предприятий
При передаче электроэнергии от электростанции к потребителю, т.е. при прохождении по проводам электрического тока, в ЛЭП возникает потеря напряжения, под которой понимают разность напряжений в начале U1 и в конце U2 линии:
 (1)
Потеря напряжения может быть определена и таким образом
(1)
Потеря напряжения может быть определена и таким образом
 (2)
где I - величина токе в линии передачи;
R - сопротивление проводов линии.
Необходимо отметить, что потеря напряжения в ЛЭП ухудшает работу электроприемников. Так, при уменьшении напряжения на 10% от номинального, световой поток ламп снижается на 30%. Поскольку вращающий момент на валy асинхронных двигателей пропорционален квадрату напряжения на его зажимах, то он значительно уменьшается при снижении питающего напряжения. А это отрицательно сказывается на работе производственных механизмов.
ГОСТом нормируются допустимые отклонения напряжения в проц.:
а) на зажимах приборов рабочего освещения, в т.ч. и прожекторного, от ‑2,5 до +5 % от номинального;
б) не электродвигателях от -5 до +10% от номинального;
в) на зажимах остальных приемников электрической энергии в пределах ±5% от номинального.
В связи с этим потерю напряжения, при расчетах выражают часто не в вольтах, а в процентах
(2)
где I - величина токе в линии передачи;
R - сопротивление проводов линии.
Необходимо отметить, что потеря напряжения в ЛЭП ухудшает работу электроприемников. Так, при уменьшении напряжения на 10% от номинального, световой поток ламп снижается на 30%. Поскольку вращающий момент на валy асинхронных двигателей пропорционален квадрату напряжения на его зажимах, то он значительно уменьшается при снижении питающего напряжения. А это отрицательно сказывается на работе производственных механизмов.
ГОСТом нормируются допустимые отклонения напряжения в проц.:
а) на зажимах приборов рабочего освещения, в т.ч. и прожекторного, от ‑2,5 до +5 % от номинального;
б) не электродвигателях от -5 до +10% от номинального;
в) на зажимах остальных приемников электрической энергии в пределах ±5% от номинального.
В связи с этим потерю напряжения, при расчетах выражают часто не в вольтах, а в процентах
 (3)
Прохождение электрического тока по проводам линий электропередач приводит к необратимому преобразованию электрической энергии в тепловую, т.е. к их бесполезному нагреву. Этот нагрев происходит за счет потерь мощности Р в проводах
(3)
Прохождение электрического тока по проводам линий электропередач приводит к необратимому преобразованию электрической энергии в тепловую, т.е. к их бесполезному нагреву. Этот нагрев происходит за счет потерь мощности Р в проводах
 (4)
которые можно определить и так:
(4)
которые можно определить и так:
 (5)
Мощность Р1 (затраченная) подается на вход линии передачи от генератора и может быть определена из соотношения
(5)
Мощность Р1 (затраченная) подается на вход линии передачи от генератора и может быть определена из соотношения
 (6)
Мощность Р2 (полезная) снимается с выхода линии и передается потребителям. Её величину рассчитывают, используя выражение
(6)
Мощность Р2 (полезная) снимается с выхода линии и передается потребителям. Её величину рассчитывают, используя выражение
 (7)
Отношение этих мощностей называют коэффициентом полезного действия h
(7)
Отношение этих мощностей называют коэффициентом полезного действия h
 (8)
который характеризует экономичность работы линии электропередачи. Современные ЛЭП обеспечивают передачу электрической энергии с h=95÷98 %.
(8)
который характеризует экономичность работы линии электропередачи. Современные ЛЭП обеспечивают передачу электрической энергии с h=95÷98 %.
 Рис. 4. Принципиальная электрическая схема стенда
г) построить в масштабе по опытным данным векторные диаграммы напряжения и токов для всех исследованных режимов работы трехфазной системы.
По результатам сделать выводы о соотношении между фазными и линейными величинами; о назначении нулевого провода; о работе соединения "звезда" при всех исследованных режимах.
Контрольные вопросы и задан
1. Как соединить потребители звездой ?
2. Какие напряжения и токи называются
а) фазными; б) линейными?
3. Запишите векторные уравнения, связывающие между собой фазные и линейные напряжения.
4. Каковы соотношения между а) фазными и линейными токами; б) фазными и линейными напряжениями при симметричной нагрузке?
5. Какие функции выполняет нулевой провод ?
6. Как отразится обрыв нулевого провода на работу потребителей при несимметричной нагрузке ?
7. Как изменятся напряжения потребителей при обрыве одного из линейных проводов и отсутствии нулевого провода?
8. Построите векторную диаграмму токов и напряжений при несимметричной активно-индуктивной нагрузке.
9. По каким формулам рассчитываются мощности соединения "звезда" при симметричной и несимметричной нагрузке ?
10. Приведите пример использования симметричной (несимметричной) нагрузки, соединенной звездой в технике.
11. Соберите схему лабораторной установки.
12. Расскажите порядок выполнения лабораторной работы.
Лабораторная работа № 6
Соединение приемника треугольником в трехфазной цепи
Рис. 4. Принципиальная электрическая схема стенда
г) построить в масштабе по опытным данным векторные диаграммы напряжения и токов для всех исследованных режимов работы трехфазной системы.
По результатам сделать выводы о соотношении между фазными и линейными величинами; о назначении нулевого провода; о работе соединения "звезда" при всех исследованных режимах.
Контрольные вопросы и задан
1. Как соединить потребители звездой ?
2. Какие напряжения и токи называются
а) фазными; б) линейными?
3. Запишите векторные уравнения, связывающие между собой фазные и линейные напряжения.
4. Каковы соотношения между а) фазными и линейными токами; б) фазными и линейными напряжениями при симметричной нагрузке?
5. Какие функции выполняет нулевой провод ?
6. Как отразится обрыв нулевого провода на работу потребителей при несимметричной нагрузке ?
7. Как изменятся напряжения потребителей при обрыве одного из линейных проводов и отсутствии нулевого провода?
8. Построите векторную диаграмму токов и напряжений при несимметричной активно-индуктивной нагрузке.
9. По каким формулам рассчитываются мощности соединения "звезда" при симметричной и несимметричной нагрузке ?
10. Приведите пример использования симметричной (несимметричной) нагрузки, соединенной звездой в технике.
11. Соберите схему лабораторной установки.
12. Расскажите порядок выполнения лабораторной работы.
Лабораторная работа № 6
Соединение приемника треугольником в трехфазной цепи
 (6)
Результаты занести в таблицу.
Результаты измерений и расчетов
(6)
Результаты занести в таблицу.
Результаты измерений и расчетов

 (7)
(7) (8)
(8) Рис.2. Схема лабораторной установки
2. При отключенных потребителях (холостой ход линии) измерить напряжение на входе U1 и выходе U2 линии.
3. Тумблером подключить первый потребитель (резистор) и измерить U1, U2, I
4. Подключая последовательно остальные пять резисторов, повторить измерения U1, U2, I и все полученные результаты занести в таблицу.
Результаты измерений и расчетов
Рис.2. Схема лабораторной установки
2. При отключенных потребителях (холостой ход линии) измерить напряжение на входе U1 и выходе U2 линии.
3. Тумблером подключить первый потребитель (резистор) и измерить U1, U2, I
4. Подключая последовательно остальные пять резисторов, повторить измерения U1, U2, I и все полученные результаты занести в таблицу.
Результаты измерений и расчетов

 Рис.1. Последовательное соединение R, L, C
Напряжения на элементах при токе
Рис.1. Последовательное соединение R, L, C
Напряжения на элементах при токе  являются синусоидальными функциями времени:
являются синусоидальными функциями времени:  ,
,
 ,
,  .
.
 Рис. 3. Векторные диаграммы токов и напряжений при несимметричной активной нагрузке фаз и обрыве нейтрального (а) и линейного (б) проводов
Обрыв, например, одного "из линейных проводов А-А" или перегорание предохранителя не нем (рис. 1) при целом нейтральном проводе приводит к отключению питания потребителей только фазы А. Режим работы двух других фаз не изменяется. Однако ток в нейтральном проводе IN несколько увеличится и станет равным векторной сумме только двух фазных токов IВ и IС (рис. 3 б). Обрыв в рассматриваемом случае еще и нейтрального провода может резко сказаться на работе включенных потребителей, так как произойдет перераспределение напряжений потребителей пропорционально величинам их сопротивлений.
При коротком замыкании в одной из фаз происходит плавление предохранителя в линейном проводе этой фазы (рис.1) и трехфазная цепь автоматически переходит в рассмотренный выше режим работы с обрывом линейного провода и целым нейтральным (рис.3 б).
Исходя из вышесказанного, всегда стремятся поддерживать целостность нейтрального провода, в него никогда не ставят предохранители или выключатели.
Порядок выполнения работы
1. Собрать схему (рис.4)
2. Замкнуть рубильники Р1 и P2 и после проверки преподавателем правильности соединений в схеме включить питание.
3. Изменяя выключателями число параллельно включенных резисторов в каждом фазной приемнике добиться симметричной активной нагрузки фаз, при которой амперметры фазных токов дают одинаковые показания. Амперметр, включенный в нулевой провод, должен показать отсутствие тока. Вольтметром со щупами измерить последовательно линейные UAB, UBC, UCA и фазные UA, UB, UC напряжения. Показания всех приборов записать в таблицу.
4. Создать несимметричную активную нагрузку по фазам, измерить фазные и линейные токи и напряжения. Обратить внимание на показания амперметра в нулевом проводе. Показания записать в таблицу.
Рис. 3. Векторные диаграммы токов и напряжений при несимметричной активной нагрузке фаз и обрыве нейтрального (а) и линейного (б) проводов
Обрыв, например, одного "из линейных проводов А-А" или перегорание предохранителя не нем (рис. 1) при целом нейтральном проводе приводит к отключению питания потребителей только фазы А. Режим работы двух других фаз не изменяется. Однако ток в нейтральном проводе IN несколько увеличится и станет равным векторной сумме только двух фазных токов IВ и IС (рис. 3 б). Обрыв в рассматриваемом случае еще и нейтрального провода может резко сказаться на работе включенных потребителей, так как произойдет перераспределение напряжений потребителей пропорционально величинам их сопротивлений.
При коротком замыкании в одной из фаз происходит плавление предохранителя в линейном проводе этой фазы (рис.1) и трехфазная цепь автоматически переходит в рассмотренный выше режим работы с обрывом линейного провода и целым нейтральным (рис.3 б).
Исходя из вышесказанного, всегда стремятся поддерживать целостность нейтрального провода, в него никогда не ставят предохранители или выключатели.
Порядок выполнения работы
1. Собрать схему (рис.4)
2. Замкнуть рубильники Р1 и P2 и после проверки преподавателем правильности соединений в схеме включить питание.
3. Изменяя выключателями число параллельно включенных резисторов в каждом фазной приемнике добиться симметричной активной нагрузки фаз, при которой амперметры фазных токов дают одинаковые показания. Амперметр, включенный в нулевой провод, должен показать отсутствие тока. Вольтметром со щупами измерить последовательно линейные UAB, UBC, UCA и фазные UA, UB, UC напряжения. Показания всех приборов записать в таблицу.
4. Создать несимметричную активную нагрузку по фазам, измерить фазные и линейные токи и напряжения. Обратить внимание на показания амперметра в нулевом проводе. Показания записать в таблицу.
 Рис. 2. Векторные диаграммы токов и напряжений: при симметричной (а) и несимметричной (б) активной нагрузке фаз
При несимметричной нагрузке фаз нарушается равенство фазных токов IА, IВ, IС и появляется ток IN, в нейтральном проводе (рис. 2 б).
Следует отметить, что при симметричной и несимметричной активной нагрузке фаз (рис. 2 а, б) наличие целого нейтрального провода обеспечивало постоянство фазных и линейных напряжений. Причем между этими напряжениями существует следующая зависимость:
Рис. 2. Векторные диаграммы токов и напряжений: при симметричной (а) и несимметричной (б) активной нагрузке фаз
При несимметричной нагрузке фаз нарушается равенство фазных токов IА, IВ, IС и появляется ток IN, в нейтральном проводе (рис. 2 б).
Следует отметить, что при симметричной и несимметричной активной нагрузке фаз (рис. 2 а, б) наличие целого нейтрального провода обеспечивало постоянство фазных и линейных напряжений. Причем между этими напряжениями существует следующая зависимость:
 , (5)
которая легко может быть установлена из векторных диаграмм.
При несимметричной активной нагрузке и обрыве нейтрального провода фазные токи изменяются таким образом, чтобы их векторная сумма (2) стала разной нулю. Это приводит к смещению потенциала нейтральной точки и к нарушению равенстве между фазными напряжениями - фаза с большим сопротивлением оказывается под повышенным напряжением, что может привести к аварийной ситуации. Векторную диаграмму в этом случае строят по опытным данным методом засечек (рис. 3 а). Сначала вычерчивают треугольник линейных напряжений UAB, UBC, UCA, которые сохранили свое равенство. Затем из соответствующих вершин треугольника радиусами, равными измеренным фазным напряжениям UA, UC, UC, описывают дуги, пересечение которых определяет положение нейтральной точки.
, (5)
которая легко может быть установлена из векторных диаграмм.
При несимметричной активной нагрузке и обрыве нейтрального провода фазные токи изменяются таким образом, чтобы их векторная сумма (2) стала разной нулю. Это приводит к смещению потенциала нейтральной точки и к нарушению равенстве между фазными напряжениями - фаза с большим сопротивлением оказывается под повышенным напряжением, что может привести к аварийной ситуации. Векторную диаграмму в этом случае строят по опытным данным методом засечек (рис. 3 а). Сначала вычерчивают треугольник линейных напряжений UAB, UBC, UCA, которые сохранили свое равенство. Затем из соответствующих вершин треугольника радиусами, равными измеренным фазным напряжениям UA, UC, UC, описывают дуги, пересечение которых определяет положение нейтральной точки.
 ,
где
,
где  - соответственно активная, индуктивная и емкостная составляющая вектора напряжения на входе цепи.
Из этого выражения следует, что при известных
- соответственно активная, индуктивная и емкостная составляющая вектора напряжения на входе цепи.
Из этого выражения следует, что при известных  , вектор
, вектор  может быть получен построением векторной диаграммы. Свойства рассматриваемой цепи, а, следовательно, и вид векторной диаграммы, будет зависеть от соотношений между индуктивным и емкостным сопротивлениями
может быть получен построением векторной диаграммы. Свойства рассматриваемой цепи, а, следовательно, и вид векторной диаграммы, будет зависеть от соотношений между индуктивным и емкостным сопротивлениями
 ;
;  ,
где ω – угловая частота;
f – частота питающей сети, Гц (f=50Гц);
L – индуктивность катушки, Гн;
C – емкость конденсатора, Ф;
На рис. 2, а показана векторная диаграмма для случая UL> UC, (xL > xC). Построение этой диаграммы начинают, откладывая в произвольном направлении вектор тока
,
где ω – угловая частота;
f – частота питающей сети, Гц (f=50Гц);
L – индуктивность катушки, Гн;
C – емкость конденсатора, Ф;
На рис. 2, а показана векторная диаграмма для случая UL> UC, (xL > xC). Построение этой диаграммы начинают, откладывая в произвольном направлении вектор тока  . Затем из точки О откладывают вектор
. Затем из точки О откладывают вектор  , совпадающий по фазе с
, совпадающий по фазе с  , опережающий вектор тока на
, опережающий вектор тока на  , и вектор
, и вектор  , отстающий от
, отстающий от  и
и  Складывая векторно
Складывая векторно  и
и  .
Угол сдвига фаз φ между напряжением
.
Угол сдвига фаз φ между напряжением  Рис. 2. Векторная диаграмма (а), треугольники сопротивлений (б) и мощностей (в) для случая
Прямоугольный треугольник OAB называют треугольником напряжений.
Если модули напряжений, входящие в этот треугольник, разделить на модуль тока, то получим значения активного R, реактивного X и полного Z сопротивлений:
Рис. 2. Векторная диаграмма (а), треугольники сопротивлений (б) и мощностей (в) для случая
Прямоугольный треугольник OAB называют треугольником напряжений.
Если модули напряжений, входящие в этот треугольник, разделить на модуль тока, то получим значения активного R, реактивного X и полного Z сопротивлений:
 ;
;  ;
;  , (2)
используя которые можно в определенном масштабе построить треугольник сопротивлений (рис 2, б). Из рассмотрения этого треугольника следует, что
, (2)
используя которые можно в определенном масштабе построить треугольник сопротивлений (рис 2, б). Из рассмотрения этого треугольника следует, что
 Для получения треугольника мощностей (рис. 2, в) умножив модули напряжений
Для получения треугольника мощностей (рис. 2, в) умножив модули напряжений  ,
,  и
и  на модуль тока I:
на модуль тока I:
 ;
;  ;
;  .
Где S – полная мощность цепи;
P – активная мощность цепи;
Q – реактивная мощность, равная Q= QL- QC.
Выражая значения Ua и UP через U (из прямоугольного треугольника САВ), будем иметь
.
Где S – полная мощность цепи;
P – активная мощность цепи;
Q – реактивная мощность, равная Q= QL- QC.
Выражая значения Ua и UP через U (из прямоугольного треугольника САВ), будем иметь
 ,
,  ,
,
 (3)
Хотя все три мощности имеют одну и туже размерность – "Вольт-Ампер", для их различия введены следующие наименования этой единицы измерения:
а) для P – "Ватт" (Вт);
б) для Q – "Вольт-Ампер-реактивный" (вар);
в) для S – "Вольт-Ампер" (ВА).
При рассмотрении случая, когда XL< XC, необходимо иметь в виду, что порядок построения векторной диаграммы аналогичен рассмотренному выше. Однако, т.к. UL< UC, угол φ принимает отрицательные значения (напряжение отстает по фазе от
(3)
Хотя все три мощности имеют одну и туже размерность – "Вольт-Ампер", для их различия введены следующие наименования этой единицы измерения:
а) для P – "Ватт" (Вт);
б) для Q – "Вольт-Ампер-реактивный" (вар);
в) для S – "Вольт-Ампер" (ВА).
При рассмотрении случая, когда XL< XC, необходимо иметь в виду, что порядок построения векторной диаграммы аналогичен рассмотренному выше. Однако, т.к. UL< UC, угол φ принимает отрицательные значения (напряжение отстает по фазе от  ).
).

 . (2)
Напряжение между началом я концом каждого потребителя, или между линейным и нейтральным проводом называется фазным напряжением (UФ) и обозначается соответственно: UA, UB, UC. Напряжение между началами двух потребителей или между двумя линейными проводами называется линейным напряжением (UЛ) и обозначается соответственно UAB, UBC, UCA.
В общем случае фазные и линейные напряжения связаны между собой согласно 2-му закону Кирхгофа:
. (2)
Напряжение между началом я концом каждого потребителя, или между линейным и нейтральным проводом называется фазным напряжением (UФ) и обозначается соответственно: UA, UB, UC. Напряжение между началами двух потребителей или между двумя линейными проводами называется линейным напряжением (UЛ) и обозначается соответственно UAB, UBC, UCA.
В общем случае фазные и линейные напряжения связаны между собой согласно 2-му закону Кирхгофа:
 ;
;  ;
;  . (3)
Каждый из однофазных потребителей в трехфазной цепи характеризуется величинами полного сопротивления ZA, ZB, ZC и коэффициентами мощности cos φA, cos φВ, cos φС. При численном равенстве полных сопротивлений фазных нагрузок и равенстве их коэффициентов мощности имеет место симметричная нагрузка фаз. Нарушение хотя бы одного из отмеченных равенств создает несимметричную нагрузку.
Для потребителя каждой фазы справедливы, в общем случае, следующие зависимости:
. (3)
Каждый из однофазных потребителей в трехфазной цепи характеризуется величинами полного сопротивления ZA, ZB, ZC и коэффициентами мощности cos φA, cos φВ, cos φС. При численном равенстве полных сопротивлений фазных нагрузок и равенстве их коэффициентов мощности имеет место симметричная нагрузка фаз. Нарушение хотя бы одного из отмеченных равенств создает несимметричную нагрузку.
Для потребителя каждой фазы справедливы, в общем случае, следующие зависимости:
 ,
,  ,
,  . (4)
В случае симметричной активной нагрузки фазные токи IА, IВ, IС равны друг другу по величине и на векторной диаграмме совпадают по направлению с соответствующими фазными напряжениями UAB, UBC, UCA (рис. 2, а): Тока в нейтральной проводе IN в этом случае не будет, что может быть подтверждено графическим решением векторного уравнения (2).
. (4)
В случае симметричной активной нагрузки фазные токи IА, IВ, IС равны друг другу по величине и на векторной диаграмме совпадают по направлению с соответствующими фазными напряжениями UAB, UBC, UCA (рис. 2, а): Тока в нейтральной проводе IN в этом случае не будет, что может быть подтверждено графическим решением векторного уравнения (2).
 (1)
При установлении соотношения по 1-му закону Кирхгофа между фазными токами потребителей IА, IВ, IС током в нейтральном проводе IN принято, что фазные токи всегда условно направлены к нейтральной точке соединения N, а ток в нейтральном проводе - от этой точки (рис.1, б):
(1)
При установлении соотношения по 1-му закону Кирхгофа между фазными токами потребителей IА, IВ, IС током в нейтральном проводе IN принято, что фазные токи всегда условно направлены к нейтральной точке соединения N, а ток в нейтральном проводе - от этой точки (рис.1, б):
 , т.е.
, т.е.  и
и  , может быть значительно больше, чем напряжение, приложенное к цепи.
Порядок построения векторной диаграммы сохраняется прежним. Согласно условию возникновения резонанса напряжений
, может быть значительно больше, чем напряжение, приложенное к цепи.
Порядок построения векторной диаграммы сохраняется прежним. Согласно условию возникновения резонанса напряжений
 ,
этот режим может быть получен при изменении частоты питающего напряжения, величины индуктивности или емкости соответствующих элементов рассматриваемой цепи.
Порядок выполнения работы
1. Собрать схему в соответствии с рис.3 и после проверки ее преподавателем замкнуть рубильник на стенде.
,
этот режим может быть получен при изменении частоты питающего напряжения, величины индуктивности или емкости соответствующих элементов рассматриваемой цепи.
Порядок выполнения работы
1. Собрать схему в соответствии с рис.3 и после проверки ее преподавателем замкнуть рубильник на стенде.
 Рис. 3. Электрическая схема лабораторной установки
2. Измерить действующие значения тока в цепи, а также напряжений на входе цепи, на резисторе UR10, катушке индуктивности UK, батарее конденсаторов UC при замкнутых тумблерах: а) P1; б) P1 и P2; в) P1, P2 и P3. Полученные данные занести в табл.1.
Результаты измерений Таблица 1.
Рис. 3. Электрическая схема лабораторной установки
2. Измерить действующие значения тока в цепи, а также напряжений на входе цепи, на резисторе UR10, катушке индуктивности UK, батарее конденсаторов UC при замкнутых тумблерах: а) P1; б) P1 и P2; в) P1, P2 и P3. Полученные данные занести в табл.1.
Результаты измерений Таблица 1.
 Рис. 4. Расчетная схема замещения
Поэтом для получения достоверных результатов необходимо выделить активную и индуктивную составляющие напряжений на катушке
Рис. 4. Расчетная схема замещения
Поэтом для получения достоверных результатов необходимо выделить активную и индуктивную составляющие напряжений на катушке
 ;
;  .
Активная составляющая напряжения цепи находится после этого суммированием напряжения, измеренного на резисторе R10 и и напряжения URK, полученного расчетных путем:
.
Активная составляющая напряжения цепи находится после этого суммированием напряжения, измеренного на резисторе R10 и и напряжения URK, полученного расчетных путем:
 .
Значение UP находится из соотношения UP= UL- UC.
4. полученные данные занести в табл.2 и по ним построить векторные диаграммы для трех случаев.
Результаты расчетов Таблица 2
.
Значение UP находится из соотношения UP= UL- UC.
4. полученные данные занести в табл.2 и по ним построить векторные диаграммы для трех случаев.
Результаты расчетов Таблица 2
 , определить R, XC, X1, Z, найти
, определить R, XC, X1, Z, найти  и
и  .
. , Вт (1-й и 3-й опыты) и
, Вт (1-й и 3-й опыты) и  , Вт (2-й опыт);
г) реактивную индуктивную мощность цепи:
, Вт (2-й опыт);
г) реактивную индуктивную мощность цепи:  , вар;
д) реактивную емкостную мощность конденсатора:
, вар;
д) реактивную емкостную мощность конденсатора:  , вар (3-й опыт);
е) суммарную реактивную мощность, потребляемую из сети (от генератора): Q= QL- QC,
ж) полную электрическую млщность потребителя:
, вар (3-й опыт);
е) суммарную реактивную мощность, потребляемую из сети (от генератора): Q= QL- QC,
ж) полную электрическую млщность потребителя:  , ВА;
з) коэффициент мощности цепи переменного тока:
, ВА;
з) коэффициент мощности цепи переменного тока:  ;
к) общий ток цепи:
;
к) общий ток цепи:  .
7. Для каждого опыта вычислений построить в масштабе треугольники мощностей.
8. По полученным результатам лабораторной работы сделать выводы о роли и значении коэффициента мощности в электрических цепях, необходимости и способах его повышения.
Контрольные вопросы и задания
1. Что называется коэффициентом мощности электрической цепи?
2. Поясните природу угла сдвига по фазе φ между током и напряжением в электрической цепи.
3. Как можно рассчитать величину cosφ цепи?
4. Для расчета какой мощности цепи используется значение cosφ?
5. Влияет ли величина cosφ на значение тока при неизменных напряжении и активной мощности в цепи?
6. В чем заключается технико-экономическое значение повышения cosφ?
7. Какие естественные способы повышения cosφ Вы знаете?
8. Поясните суть и методы искусственных способов повышения cosφ.
9. Влияет ли и почему значение cosφ на нагрев проводов линии электропередач?
10. Расскажите о цели и порядке проведения работы.
11. Соберите схему лабораторной установки.
.
7. Для каждого опыта вычислений построить в масштабе треугольники мощностей.
8. По полученным результатам лабораторной работы сделать выводы о роли и значении коэффициента мощности в электрических цепях, необходимости и способах его повышения.
Контрольные вопросы и задания
1. Что называется коэффициентом мощности электрической цепи?
2. Поясните природу угла сдвига по фазе φ между током и напряжением в электрической цепи.
3. Как можно рассчитать величину cosφ цепи?
4. Для расчета какой мощности цепи используется значение cosφ?
5. Влияет ли величина cosφ на значение тока при неизменных напряжении и активной мощности в цепи?
6. В чем заключается технико-экономическое значение повышения cosφ?
7. Какие естественные способы повышения cosφ Вы знаете?
8. Поясните суть и методы искусственных способов повышения cosφ.
9. Влияет ли и почему значение cosφ на нагрев проводов линии электропередач?
10. Расскажите о цели и порядке проведения работы.
11. Соберите схему лабораторной установки.
 Рис. 2. Электрическая схема лабораторной установки
2. Определить коэффициент мощности цепи, содержащей обмотку возбуждения однофазного асинхронного двигателя с активным сопротивлением R и индуктивностью L. Для этого разомкнуть тумблер P1 и P2, а затем включить стенд. Снять показания приборов и записать их в таблицу измерений и расчетов.
3. Исследовать способ повышения cosφ цепи с обмоткой возбуждения при параллельном подключении к ней электрической печи с резистивным нагревательным элементом, имеющем сопротивление Rдоб. Для этого замкнуть тумблер P1, снять показания приборов и записать их в таблицу.
4. Исследовать способ повышения cosφ цепи с обмоткой возбуждения при параллельном подключении к ней статического конденсатора, имеющего реактивное емкостное сопротивление XC. Для этого разомкнуть тумблер P1 и замкнуть тумблер P2. Снять показания приборов и записать их в таблицу.
5. Отключить стенд и показать результаты наблюдений преподавателю.
Результаты измерений и расчетов Таблица 5
Рис. 2. Электрическая схема лабораторной установки
2. Определить коэффициент мощности цепи, содержащей обмотку возбуждения однофазного асинхронного двигателя с активным сопротивлением R и индуктивностью L. Для этого разомкнуть тумблер P1 и P2, а затем включить стенд. Снять показания приборов и записать их в таблицу измерений и расчетов.
3. Исследовать способ повышения cosφ цепи с обмоткой возбуждения при параллельном подключении к ней электрической печи с резистивным нагревательным элементом, имеющем сопротивление Rдоб. Для этого замкнуть тумблер P1, снять показания приборов и записать их в таблицу.
4. Исследовать способ повышения cosφ цепи с обмоткой возбуждения при параллельном подключении к ней статического конденсатора, имеющего реактивное емкостное сопротивление XC. Для этого разомкнуть тумблер P1 и замкнуть тумблер P2. Снять показания приборов и записать их в таблицу.
5. Отключить стенд и показать результаты наблюдений преподавателю.
Результаты измерений и расчетов Таблица 5
 , Ом;
, Ом; , Ом;
, Ом; (1)
Эта мощность (1) передается по линии электропередач (ЛЭП) к потребителям большинство из которых имеет в своих конструкциях обмотки различного типа и вследствие этого обладают активно-индуктивным электрическим сопротивлением (электродвигатели, сварочные и силовые трансформаторы, электрические печи, установки электрического освещения, электромагниты различного
(1)
Эта мощность (1) передается по линии электропередач (ЛЭП) к потребителям большинство из которых имеет в своих конструкциях обмотки различного типа и вследствие этого обладают активно-индуктивным электрическим сопротивлением (электродвигатели, сварочные и силовые трансформаторы, электрические печи, установки электрического освещения, электромагниты различного  (2)
Таким образом, только часть электрической мощности, вырабатываемой генератором и подводимой к потребителю, необратимо преобразуется в поленую активную мощность потребителя Р: механическую, тепловую, световую и т.д. Степень полезного использования потребителем электрической мощности генератора и определяется величиной косинуса. угла сдвига фаз между током I и напряжением U:
(2)
Таким образом, только часть электрической мощности, вырабатываемой генератором и подводимой к потребителю, необратимо преобразуется в поленую активную мощность потребителя Р: механическую, тепловую, световую и т.д. Степень полезного использования потребителем электрической мощности генератора и определяется величиной косинуса. угла сдвига фаз между током I и напряжением U:
 , (3)
Который часто называют коэффициентом мощности потребителя или коэффициентом мощности цепи переменного тока.
Процесс передачи электрической мощности от генератора к потребителю, имеющему активно-индуктивное сопротивление, характеризуется помимо активной мощности еще и реактивной мощностью:
, (3)
Который часто называют коэффициентом мощности потребителя или коэффициентом мощности цепи переменного тока.
Процесс передачи электрической мощности от генератора к потребителю, имеющему активно-индуктивное сопротивление, характеризуется помимо активной мощности еще и реактивной мощностью:
 (4)
Реактивная мощность идет на создание индуктивными катушками потребителя переменных магнитных полей. Особенностью является, что этой мощностью непрерывно обмениваются между собой ЛЭП, генератор и потребитель.
Между рассмотренными мощностями S, P и Q существует зависимость:
(4)
Реактивная мощность идет на создание индуктивными катушками потребителя переменных магнитных полей. Особенностью является, что этой мощностью непрерывно обмениваются между собой ЛЭП, генератор и потребитель.
Между рассмотренными мощностями S, P и Q существует зависимость:
 (5)
Очевидно, что генератор выгодно эксплуатировать так, чтобы вырабатываемая им электрическая энергия полностью использовалась у потребителя на совершение полезной, нужной людям работы. Такое использование мощности генератора происходит только тогда, когда коэффициент мощности потребителя равен единице (cosφ=1);
(5)
Очевидно, что генератор выгодно эксплуатировать так, чтобы вырабатываемая им электрическая энергия полностью использовалась у потребителя на совершение полезной, нужной людям работы. Такое использование мощности генератора происходит только тогда, когда коэффициент мощности потребителя равен единице (cosφ=1);
 Всякое уменьшение cosφ, значение которого определяется соотношением активного и индуктивного сопротивлений у потребителя, приводит к неполному использованию мощности генератора в полезных целях, т.е. наряду с активной электрической мощностью для потребителя генератор должен вырабатывать еще и реактивную мощность. Кроме того, если потребитель рассчитан на неизменное напряжение и мощность P, то потребляемый им ток, который также является током, всей цепи и генератора, будет тем больше, чем меньше коэффициент мощности:
Всякое уменьшение cosφ, значение которого определяется соотношением активного и индуктивного сопротивлений у потребителя, приводит к неполному использованию мощности генератора в полезных целях, т.е. наряду с активной электрической мощностью для потребителя генератор должен вырабатывать еще и реактивную мощность. Кроме того, если потребитель рассчитан на неизменное напряжение и мощность P, то потребляемый им ток, который также является током, всей цепи и генератора, будет тем больше, чем меньше коэффициент мощности:
 . (6)
Таким образом, при низких значениях коэффициента мощности народному хозяйству наносится определенный технико-экономический ущерб, поскольку из-за повышенных значений тока (6) и загрузки цепи значительными потоками реактивной мощности:
. (6)
Таким образом, при низких значениях коэффициента мощности народному хозяйству наносится определенный технико-экономический ущерб, поскольку из-за повышенных значений тока (6) и загрузки цепи значительными потоками реактивной мощности:
 Рисунок 1. Треугольники мощностей
а) для исходной цепи с активно-индуктивным сопротивлением;
б) при параллельном подключении к цепи активного сопротивления;
в) при параллельном подключении к цепи емкостного сопротивления.
Порядок выполнения работы
1. Собрать на стенде электрическую схему лабораторной работы (рис. 2) и дать ее проверить преподавателю.
Рисунок 1. Треугольники мощностей
а) для исходной цепи с активно-индуктивным сопротивлением;
б) при параллельном подключении к цепи активного сопротивления;
в) при параллельном подключении к цепи емкостного сопротивления.
Порядок выполнения работы
1. Собрать на стенде электрическую схему лабораторной работы (рис. 2) и дать ее проверить преподавателю.