Студентов заочной формы обучения
Утверждаю
Председатель ПЦК
Кондаков С.А.
__________________
« ___» __________ 2013 г.
Вопросы к промежуточной аттестации
По дисциплине «Математика»
Для специальностей 1 курса
Семестр
1. Назовите числовые множества.
2. Множество натуральных чисел.
3. Множество рациональных чисел.
Ответ: Множество рациональных чисел обозначается заглавной английской буквой Q (кью).
Множество Q включает в себя множество целых чисел (Z) и натуральных чисел (N).
Любое рациональное число можно представить в виде дроби, у которой числитель принадлежит целым числам, а знаменатель - натуральным.
a/b, где a ∈ Z ( a принадлежит целым числам ), b∈N ( b принадлежит натуральным числам ).
- 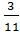 =
= 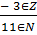 ; - 5
; - 5  =
= 
Множество рациональных чисел обозначается Q (от англ. Quotient «частное») и может быть записано в таком виде:
Q={mn∣m∈Z,n∈N}.
При этом оказывается, что разные записи могут представлять одну и ту же дробь, например, 34 и 912, (все дроби, которые можно получить друг из друга умножением или делением числителя и знаменателя на одно и то же натуральное число, представляют одно и то же рациональное число). Поскольку делением числителя и знаменателя дроби на их наибольший общий делитель можно получить единственное несократимое представление рационального числа, то можно говорить об их множестве как о множестве несократимых дробей со взаимно простыми целым числителем и натуральным знаменателем:
|
|
|
Q={mn∣m∈Z,n∈N,gcd(m,n)=1}.
Здесь gcd(m,n) — наибольший общий делитель чисел m и n.
Множество рациональных чисел является естественным обобщением множества целых чисел. Легко видеть, что если у рационального числа a=mn знаменатель n=1, то a=m является целым числом.
Множество рациональных чисел располагается всюду плотно на числовой оси: между любыми двумя различными рациональными числами расположено хотя бы одно рациональное число (а значит, и бесконечное множество рациональных чисел). Тем не менее, оказывается, что множество рациональных чисел имеет счётную мощность (то есть все его элементы можно перенумеровать). Со времён древних греков известно о существовании чисел, не представимых в виде дроби: они доказали, что не существует рационального числа, квадрат которого равен двум. Недостаточность рациональных чисел для выражения всех величин привела в дальнейшем к понятию вещественного числа. В отличие от множества вещественных чисел (которое соответствует одномерному пространству), множество рациональных чисел нульмерно.
1. Коммутативность умножения. От перемены мест рациональных множителей произведение не меняется.
∀a,b∈Q a⋅b=b⋅a
2. Ассоциативность умножения. Порядок перемножения трёх рациональных чисел не влияет на результат.
|
|
|
∀a,b,c∈Q (a⋅b)⋅c=a⋅(b⋅c)
3 Наличие единицы . Существует рациональное число 1, которое сохраняет любое другое рациональное число при умножении.
∃1∈Q ∀a∈Q a⋅1=a
4 Наличие обратных чисел . Любое ненулевое рациональное число имеет обратное рациональное число, умножение на которое даёт 1.
∀a∈Q ∃a−1∈Q a⋅a−1=1
5 Дистрибутивность умножения относительно сложения. Операция умножения согласована с операцией сложения посредством распределительного закона:
∀a,b,c∈Q (a+b)⋅c=a⋅c+b⋅c
6 Связь отношения порядка с операцией умножения. Левую и правую части рационального неравенства можно умножать на одно и то же положительное рациональное число.
∀a,b,c∈Q c>0∧a<b⇒a⋅c<b⋅c
4. Множество действительных чисел.
Ответ: Если множество рациональных чисел дополнить множеством иррациональных чисел, то вместе они составят множество действительных чисел. Множество действительных чисел обычно обозначают буквой R; используют также символическую запись (-оо, +оо) или (-оо, оо).
Множество действительных чисел - это множество конечных и бесконечных десятичных дробей; конечные десятичные дроби и бесконечные десятичные периодические дроби — рациональные числа, а бесконечные десятичные непериодические дроби — иррациональные числа.
|
|
|
Каждое действительное число можно изобразить точкой на координатной прямой. Верно и обратное: каждая точка координатной прямой имеет действительную координату. Математики обычно, говорят так: между множеством R действительных чисел и множеством точек координатной прямой установлено взаимно однозначное соответствие. Координатная прямая есть геометрическая модель множества действительных чисел; по этой причине для координатной прямой часто используют термин числовая прямая.
1. Действительные числа состоят из положительных действительных чисел, отрицательных действительных чисел и числа ноль.
R = R − ∪ {0} ∪ R +
2. Действительные числа включают в себя рациональные и иррациональные числа.
R = Q ∪ I
R—множество действительных чисел.
Множество R содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью. Так, 1/2= 0,5 (= 0,500...), 1/3=0,333... — рациональные числа.
Действительные числа, не являющиеся рациональными, называются иррационалъными.
|
|
|
3. Множество R непрерывное. Пусть множество R разбито на два непустых класса А и В таких, что каждое действительное число содержится только в одном классе и для каждой пары чисел aєА и bєВ выполнено неравенство a<b. Тогда (свойство непрерывности) существует единственное число с, удовлетворяющее неравенству a≤с≤b (aєA, bєВ). Оно отделяет числа класса. A от чисел класса В.Число с является либо наибольшим числом в классе А (тогда в классе В нет наименьшего числа), либо наименьшим числом в классе В (тогда в классе А нет наибольшего).
Свойство непрерывности позволяет установить взаимно-однозначное соответствие между множеством всех действительных чисел и множеством всех точек прямой. Это означает, что каждому числу хєR соответствует определенная (единственная) точка числовой оси и, наоборот, каждой точке оси соответствует определенное (единственное) действительное число. Поэтому вместо слова «число» часто говорят «точка».
5. множество комплексных чисел.
6. Правила сложения, вычитания комплексных чисел.
7. Умножение комплексных чисел.
8. Деление комплексных чисел.
9. Геометрическая интерпретация комплексного числа.
10. Понятие корня n-ой степени из числа.
Ответ:
11. Понятие степени с рациональным показателем и их свойства.
Ответ: рациональные числа - это целые и дробные числа (обыкновенные дроби, конечные десятичные дроби и бесконечные периодические дроби).
12. Свойства корня n-ой степени
Ответ: Теорема 1 . корень n-ой степени (n = 2,3,4,…) из произведения двух неотрицательных чисел равен произведению корней n-ой степени:
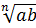 =
= 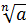 +
+ 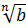
Доказательство: Введем следующие обозначения. 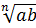 = х;
= х; 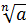 =y;
=y; 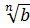 =z.
=z.
Нам надо доказать, что для неотрицательных чисел x, y,z. Выполняют равенство x-yz/
Так как 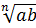 = x,
= x, 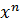 = ab. Так как
= ab. Так как 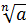 =y, то
=y, то 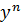 = a.
= a.
Так как 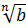 =z, то
=z, то 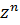 = b
= b
Итак, 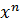 = ab.
= ab. 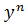 = a.
= a. 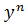 = a.
= a. 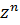 = b., тогда
= b., тогда 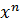 =
= 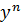
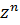 . Т.е.
. Т.е. 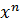 =
= 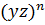
Но если степени двух неотрицательных чисел равны и показатели степеней равны, то равны и основания степеней; значит, из равенства 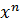 =
= 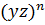 следует, что x-yz, а это и следовало доказать.
следует, что x-yz, а это и следовало доказать.
Приведем краткую запись доказательства теоремы:
| Подготовка к доказательству введения новых перемен | Перевод на более простой язык | Доказательство |
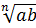 = x = x
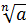 =y =y
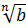 =z. =z.
| 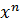 = ab. = ab.
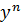 = a = a
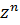 = b = b
| 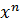 = = 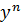 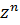
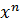 = = 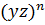 x=yz
x=yz
|
| Доказать x=yz |
Замечания:
1. Теорема 1 остается справедливой и для случая, когда подкоренное выражение представляет собой произведение более чем двух неотрицательных чисел.
2. Теорему 1 можно сформулировать, используя конструкцию "если...то» (как это принято для теорем в математике). Приведем соответствующую формулировку: если а иb — неотрицательные числа, то справедливо равенство 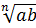 =
= 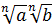 . Следующую теорему мы именно так и оформим.
. Следующую теорему мы именно так и оформим.
Теорема 2. Если a≥0; b>0 и n натуральное число, больше 1, то справидливо равенство
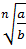 =
= 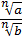
Корень из дроби равен дроби от корней
Доказательство. Приведем краткую запись доказательства теоремы 2
| Подготовка к доказательству (введения новых переменных) | Перевод на более простой язык | Доказательство |
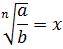
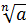 =y =y
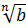 =z. =z.
| 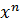 = =  . .
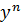 = a = a
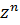 = b = b
| 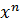 = = 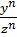
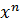 = = 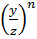 x=
x= 
|
Доказать x= 
|
ВЫ, конечно, обратили внимание на то, что доказанные два свойства корней п-й степени представляют собой обобщение известных вам из курса алгебры 8-го класса свойств квадратных корней. И если бы других свойств корней п-й степени не было, то как бы все было просто (и не очень интересно). На самом деле есть еще несколько интересных и важных свойств, которые мы обсудим в этом параграфе. Но сначала рассмотрим несколько примеров на использование теорем 1 и 2.
Пример: 1. Вычислить 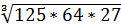
Решение. Воспользовавшись первым свойством корней (теорема 1), получим: 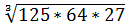 =
= 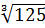 +
+ 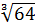 +
+ 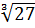 = 5*4*3 = 60.
= 5*4*3 = 60.
Замечание 3. Можно, конечно, этот пример решить по-другому, особенно если под рукой есть микрокалькулятор: перемножить числа 125, 64 и27,а затем извлечь кубический корень из полученного произведения. Но, согласитесь, предложенное решение «интеллигентнее»
Пример 2. Вычислить 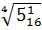
Решение. Обратим смешанное число 5 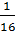 в неправильную дробь.
в неправильную дробь.
Имеем 5 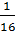 = 5
= 5 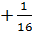 =
= 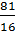 . Воспользовавшись вторым свойством корней (теорема 2), получим:
. Воспользовавшись вторым свойством корней (теорема 2), получим:
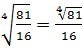 =
=  =1,5
=1,5
Пример 3. Вычислить: а) 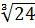
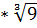 ; б)
; б) 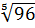 /
/ 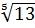
Решение. Любая формула в алгебре, как вам хорошо известно, используется не только «слева направо», но и «справа налево». Так, первое свойство корней означает, что 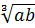 можно представить в виде
можно представить в виде 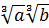 и наоборот,
и наоборот, 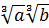 можно заменить выражением
можно заменить выражением 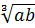 . То же относится и ко второму свойству корней. Учитывая это, выполним вычисления:
. То же относится и ко второму свойству корней. Учитывая это, выполним вычисления:
а)  =
= 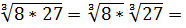 2*3 = 6
2*3 = 6
b) 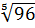 /
/ 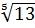 =
= 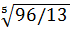 =
= 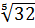 = 2.
= 2.
Пример 4. Выполнить действия: а) 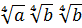 ; б)
; б) 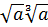 .
.
Решение, а) Имеем: 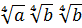 =
= 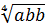 =
= 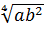
б) Теорема 1 позволяет нам перемножать только корни одинаковой степени, т.е. только корни с одинаковым показателем. Здесь же предлагается умножить корень 2-й степени из числа а на корень 3-й степени из того же числа. Как это делать, мы пока не знаем. Вернемся к этой проблеме позднее.
Теорема3. Если а ≥ 0, k натуральное число и n - нату3ральное число, больше 1, то справедливо равенство ( 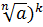 =
= 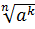
Иными словами, чтобы возвести корень в натуральную степень, достаточно возвести в эту степень подкоренное выражение.
Это — следствие теоремы 1. В самом деле, например, для к = 3 получаем: ( 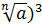 =
= 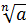 *
* 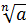 *
* 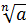 =
= 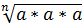 =
= 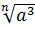 Точно так же можно рассуждать в случае любого другого натурального значения показателя к.
Точно так же можно рассуждать в случае любого другого натурального значения показателя к.
Теорема 4. Если а ≥ 0 и n, k натуральные числа, больше 1, то справедливо равенство 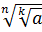 =
= 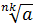 .
.
Иными словами, чтобы извлечь корень из корня, достаточно перемножить показатели корней.
Например: 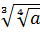 =
= 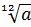 ;
; 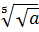 =
= 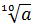 ;
;  =
= 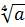 .
.
Доказательство. Как и в теореме 2, приведем краткую запись доказательства, а вы попробуйте самостоятельно сделать соответствующие комментарии, аналогичные тем, что были приведены при доказательстве теоремы 1.
| Подготовка к доказательству (введения новых переменных) | Перевод на более простой язык | Доказательство |
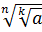 =x =x
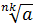 =y =y
| 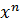 = = 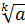 ((
(( 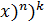 = a = a
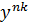 =a =a
| (( 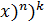 = = 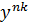
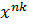 = = 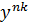 x = y
x = y
|
| Доказать x=y |
Замечание 4. благодаря доказанным теоремам, мы узнали, что над корнями можно осуществлять четыре операции: умножение, деление, возведение в степень и извлечение корня (из корня).
Операции извлечения квадратного корня.
Например, вместо 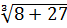 нельзя написать
нельзя написать 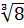 +
+ 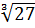 .
.
В самом деле, 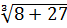 =
= 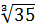 , а
, а 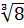 +
+ 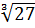 = 2+3 = 5. Но ведь очевидно, что
= 2+3 = 5. Но ведь очевидно, что 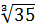 ≠ 5.
≠ 5.
Самое, пожалуй, интересное свойство корней — это то, о котором пойдет речь в следующей теореме. Учитывая особую значимость этого свойства, мы позволим себе нарушить определенный стиль формулировок и доказательств, выработанный в этом параграфе, с тем, чтобы формулировка теоремы 5 была немного «мягче», а ее доказательство — понятнее.
Теорема 5. Если показатели корня и подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится, т.е. 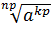 =
= 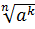 .
.
Например:
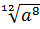 =
= 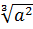 . (показатели корня и подкоренного выражения разделили на 4);
. (показатели корня и подкоренного выражения разделили на 4);
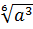 =
= 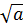 (показатели корня и подкоренного выражения разделили на 3);
(показатели корня и подкоренного выражения разделили на 3);
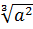 =
= 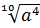 (показатели корня и подкоренного выражения умножили на 2).
(показатели корня и подкоренного выражения умножили на 2).
Доказательство: Обозначим левую часть доказываемого равенства буквой x: 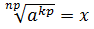 Тогда по определению корня должно выполняться равенство
Тогда по определению корня должно выполняться равенство 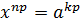 . (1)
. (1)
Обозначим правую часть доказываемого тождества буквой у: 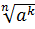 = y.
= y.
Тогда по определению корня должно выполняться равенство 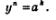
Возведем обе части последнего равенства в одну и ту же степень р; получим: 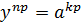 . (2).
. (2).
Итак (см. равенства (1) и (2)), 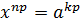 ,
, 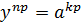 .
.
Сопоставляя эти два равенства, приходим к выводу, что 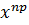 =
= 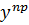 , а значит, х =у, что и требовалось доказать.
, а значит, х =у, что и требовалось доказать.
Доказанная теорема позволит нам решить ту проблему, с которой мы столкнулись выше при решении примера 5, где требовалось выполнить умножение корней с разными показателями: 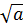 =
=  .
.
1)По теореме 5 в выражении 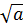 можно и показатель корня (т.е. число 2) и показатель подкоренного выражения (т.е. число 1) умножить на одно и то же натуральное число. Воспользовавшись этим, умножим оба показателя на 3; получим:
можно и показатель корня (т.е. число 2) и показатель подкоренного выражения (т.е. число 1) умножить на одно и то же натуральное число. Воспользовавшись этим, умножим оба показателя на 3; получим: 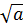 =
=  .
.
2)По теореме 5 в выражении  . можно и показатель корня (т.е. число 3) и показатель подкоренного выражения (т.е. число 1) умножить на одно и то же натуральное число. Воспользовавшись этим, умножим оба показателя на 2; получим:
. можно и показатель корня (т.е. число 3) и показатель подкоренного выражения (т.е. число 1) умножить на одно и то же натуральное число. Воспользовавшись этим, умножим оба показателя на 2; получим:  =
= 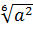
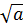 *
*  =
= 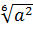 *
* 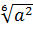 =
= 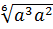 =
= 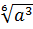
Замечание 5. все свойства корней, которые мы обсуждали в этом параграфе, рассмотрены нами только для случая, когда переменные принимают лишь неотрицательные значения? Почему пришлось сделать такое ограничение? Потому, что корень n - й степени из отрицательного числа не всегда имеет смысл — он определен только для нечетных значений n. Для таких значений показателя корня рассмотренные свойства корней верны и в случае отрицательных подкоренных выражений.
12.Свойства степеней с рациональным показателем
13. Понятие иррационального уравнения.
14. Алгоритм решения иррациональных уравнений.
15. Определения логарифмов.
16. Свойства логарифмов.
17. Логарифмирование.
18. Потенцирование.
19. Десятичные логарифмы и их свойства.
20. Логарифмы натуральные.
21. Основное логарифмическое тождество.
22. Формула перехода к логарифму с новым основанием.
23. Понятие логарифмического уравнения.
24. Понятие логарифмического неравенства.
25. Графики взаимно-обратных функций.
26. Сложная функция свойства, график функции.
27. Показательная функция и ее свойства.
28. Логарифмическая функция и ее свойства.
29. Преобразование графиков функций.
30. Радианная мера угла.
31. Понятие синуса, косинуса.
Ответ:
32. Понятие тангенса и котангенса.
33. Основное тригонометрическое тождество.
34. Формула суммы и разности синуса и косинуса.
35. Формула двойного аргумента.
36. Формула суммы синусов и косинусов.
37. Свойства и график функции синуса.
38. Свойства и график косинуса.
39. Свойства и график тангенса.
40. Свойства и график котангенса.
41. Рациональные уравнения и способы их решения.
42. Иррациональные уравнения и способы их решения.
43. Иррациональные уравнения и способы их решения.
44. Показательные неравенства, способы их решения.
45. Логарифмические уравнения и способы их решения.
46. Обратные тригонометрические функции.
47. Решение уравнения вида sin x=a
48. Решение уравнения cos x =a
49. Решение уравнения tg x=a
50. Решения уравнения ctg x=a
51. Однородные тригонометрические уравнения. Приведите пример.
52. Решение систем тригонометрических уравнений.
53. Что изучает комбинаторика.
54. Перестановки формулы.
55. Число сочетаний из n по m, формула
56. Число размещений из n по m
57. Треугольник Паскаля
58. Формула Бинома Ньютона
59. Свойства биноминальных коэффициентов
НОУ СПО
«Челябинский юридический колледж»

Утверждаю
Председатель ПЦК
Кондаков С.А.
__________________
« ___» __________ 2013 г.
Задания к контрольной работе
по дисциплине «Математика»
студентов заочной формы обучения
с применением дистанционных образовательных технологий
для специальностей 1 курса
1 семестр
Челябинск
2013
| ОДОБРЕНА на заседании предметно-цикловой комиссии «Математика, информатика и ВТ» Протокол № 1 от 30.09.2013 г. | Составлена на основе федерального государственного образовательного стандарта СПО в соответствии с учебным планом и рабочей программой дисциплины «Математика» по специальностям 1 курса |
| Председатель предметно-цикловой комиссии _________________С.А. Кондаков | |
| Составитель: Г.П. Бухарина | преподаватель предметно-цикловой комиссии «Математика, информатика и ВТ» Челябинского юридического колледжа |
| Рецензенты: Л.Н. Коврижкина Е.С. Русакова А.А. Радионов | преподаватель предметно-цикловой комиссии «Математика, информатика и ВТ» Челябинского юридического колледжа преподаватель предметно-цикловой комиссии «Математика, информатика и ВТ» Челябинского юридического колледжа директор ООО «Дефайн-групп» |
Пояснительная записка
Контрольная работа составлена на основе рабочей программы учебной дисциплины «Математика» и является частью основной образовательной программы по всем специальностям 1 курса и едина для всех форм обучения.
В структуре основной профессиональной образовательной программы учебная дисциплина «Математика» относится к общеобразовательному циклу.
В результате освоения учебной дисциплины студент должен уметь :
- использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
- для практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
- использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
- для описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков.
- использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
- для построения и исследования простейших математических моделей.
- - использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
- для исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
вычисления объемов и площадей поверхностей пространственных
В результате освоения учебной дисциплины студент должен знать :
- значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
- значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
- универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
- вероятностный характер различных процессов окружающего мира.
- В результате освоения учебной дисциплины студент должен овладевать :
общими компетенциями, включающими в себя способность
- ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
- ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
- ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
- ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
- ОК 5. Владеть информационной культурой, анализировать и оценивать информацию с использованием информационно-коммуникационных технологий.
- ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.
- ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий.
- ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.
- ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.
- ОК 10. Исполнять воинскую обязанность, в том числе с применением полученных профессиональных знаний.
Контрольная работа проводится в целях закрепления полученных теоретических знаний и выработки навыков их применения. Перед началом выполнения контрольной работы необходимо изучить содержание соответствующих учебных пособий, конспектов лекций. При выполнении контрольной работы следует руководствоваться общими указаниями по выполнению письменных работ.
Все задания для контрольной работы разделены на 5 вариантов.
Номер варианта определяется по номеру журнального списка студента (после 5-ого варианты дублируются).
Критерии оценок
Контрольная работа оценивается по пятибалльной системе.
5 баллов – работа выполнена в полном объеме, без ошибок, аккуратно оформлена.
4 балла – работа выполнена без серьезных ошибок, даны недостаточно полные объяснения.
3 балла – студентом выполнено не менее 50% задания.
2 балла – студент не справился с заданием (выполнено менее 50% задания), имеются грубые ошибки.
Вариант № 1
1. Упростить выражение 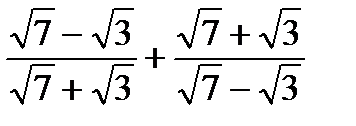 ;
;
2. Упростите выражение 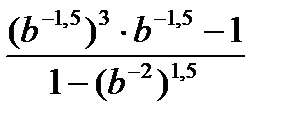
3. Найдите логарифм по основанию а числа, представленного в виде степени с основанием а: 32=9
4. Вычислить: log33
5. Определите четность или нечетность функции у =3х+3 tg x
6. Найдите область значений y=3+sin x
7. Решить уравнение: cos x = 0
8. Решить дробно-рациональное уравнение
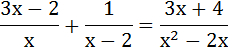
9. Решить систему неравенств
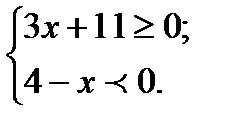
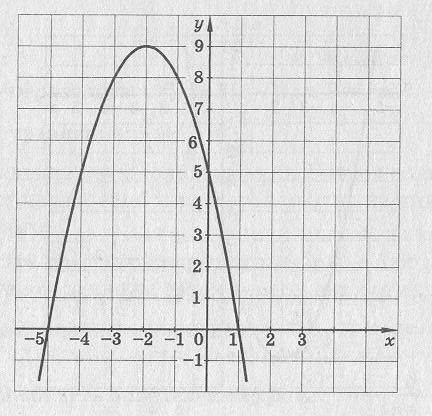
10. На рисунке изображен график некоторой функции
Выпишите те утверждения, которые считаете верными:
a) если х= -5, то у= 0;
b) функция убывает на промежутке (-∞; -2);
c) у > 0 при -5< х <1;
d) у=0 при х=5
11. Сколькими способами можно составить трехцветный полосатый флаг, если имеются 5 различных цветов ткани, но один из цветов обязательно должен быть синим?
Вариант № 2
1. Упростить выражение 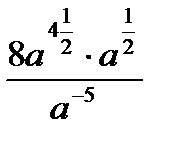
2. Упростите выражение 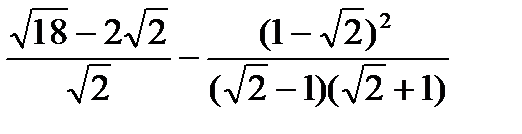
3. Найдите логарифм с основанием а числа, представленного в виде степени с основанием а: 42=16
4. Вычислить: log28
5. Определите четность или нечетность функции у=2х+3sinx
6. Найдите область определения y=2sin x
7. Решить уравнение: cos x = -1
8. Решить дробно-рациональное уравнение
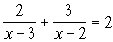
9. Решить систему неравенств
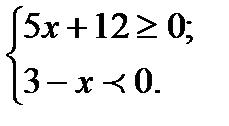
10. Укажите промежутки возрастания данной функции:
| 3 |
| X |
| 0 |
| -2 |
| 2 |
| 4 |
| y |
11. В школьной библиотеке хранятся 18 различных книг по истории и 5 — по физике. Ученику 10-го класса надо прочитать любые 4 книги по истории и 2 — по физике. Сколькими различными способами он может это сделать в школьной библиотеке?
Вариант № 3
1. Упростить выражение 
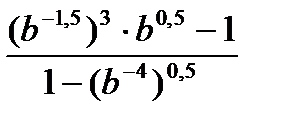
2. Упростите выражение 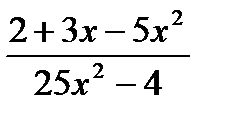
3. Найдите логарифм по основанию а числа, представленного в виде степени с основанием а: 53=125
4. Вычислить: log216
5. Определите четность или нечетность функции у =5х+3ctg x
6. Найдите область определения y=2sin x
7. Решить уравнение: cos x = 2
8. Решить дробно-рациональное уравнение
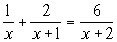
9. Решить систему неравенств
5х+6≤1
2x+1 ≥ 3
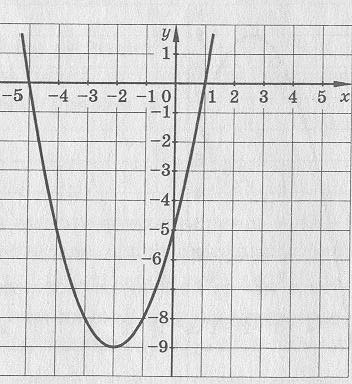
10. На рисунке изображен график некоторой функции
Выпишите те утверждения, которые считаете верными:
a) если х= -5, то у= 0;
b) функция убывает на промежутке (-∞; -2);
c) у > 0 при х <-2;
d) у=- 2 при х=-9
11. В клетке сидит 7 мартышек. Служитель зоопарка должен дать каждой из них по два любых плода. При этом надо учесть, что капризные мартышки не любят получать одинаковые наборы. Сможет служитель угостить всех мартышек, если у него есть только бананы, яблоки и персики? Сколько еще других сортов фруктов надо иметь служителю, чтобы угостить всех мартышек?
Вариант № 4
1. Упростить выражение 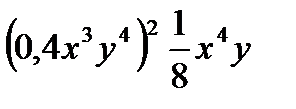
2. Упростите выражение 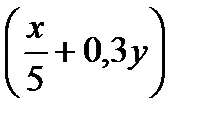
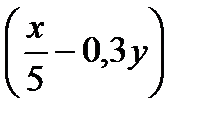
3. Найдите логарифм по основанию а числа, представленного в виде степени с основанием а: 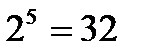
4. Вычислить: log28
5. Определите четность или нечетность функции у=2+3cos x
6. Найдите область определения y=5+sin 2x
7. Решить уравнение: cos x = 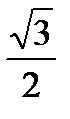
8. Решить дробно-рациональное уравнение
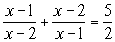
9. Решить систему неравенств
4х+4≥ 0
6–4х ≥ 0
10. Построить график функции у= -х2 + 6х – 5 и укажите наибольшее значение этой функции
11. В двух стаканах находится 10 синих и 5 красных карандашей. Сколькими способами можно выбрать 2 синих и 2 красных карандаша?
Указания:
При выполнении задания 9, необходимо представить построенный график в сканированном виде.
Вариант № 5
1. Представьте выражение в виде степени 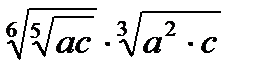 .
.
2. Раскройте скобки 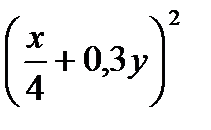
3. Найдите логарифм по основанию а числа, представленного в виде степени с основанием а: 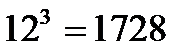
4. Вычислить: log232
5. Определите четность или нечетность функции у =8+5sin x
6. Найдите область определения y=5+sin 2x
7. Решить уравнение: sin x - 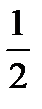 = 0
= 0
8. Решить дробно-рациональное уравнение
 = 0
= 0
9. Решить систему неравенств

10. Построить график функции у= -х2 + 6х – 5 и укажите наибольшее значение этой функции
11. У Пети есть 7 монет по 1 рублю и 3 монеты по 2 рубля. Петя случайным образом выбирает 1 монету номиналом 1 рубль и 1 монету номиналом 2 рубля. Сколькими способами он может это сделать?
Указания:
При выполнении задания 9, необходимо представить построенный график в сканированном виде.
Дата добавления: 2020-11-15; просмотров: 79; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
