Построение изометрической проекции многогранника
Построение в изометрии плоских фигур
Задан правильный шестиугольник АВСDЕF, расположенный параллельно горизонтальной плоскости проекций Н (П1).
а) Строим изометрические оси (рис.3).
б) Коэффициент искажения по осям в изометрии равен 1, поэтому от точки О0 по осям откладываем натуральные величины отрезков: А0О0 = АО; О0D0 = ОD; К0О0 = КО; О0Р0 = ОР.
в) Линии, параллельные координатным осям, проводятся в изометрии также параллельно соответствующим изометрическим осям в натуральную величину.
В нашем примере стороны ВС и FЕпараллельны оси Х.
В изометрии они вычерчиваются также параллельно оси Х в натуральную величину В0С0 = ВС; F0Е0= FЕ.
г) Соединяя полученные точки, получим изометрическое изображение шестиугольника в плоскости Н (П1).
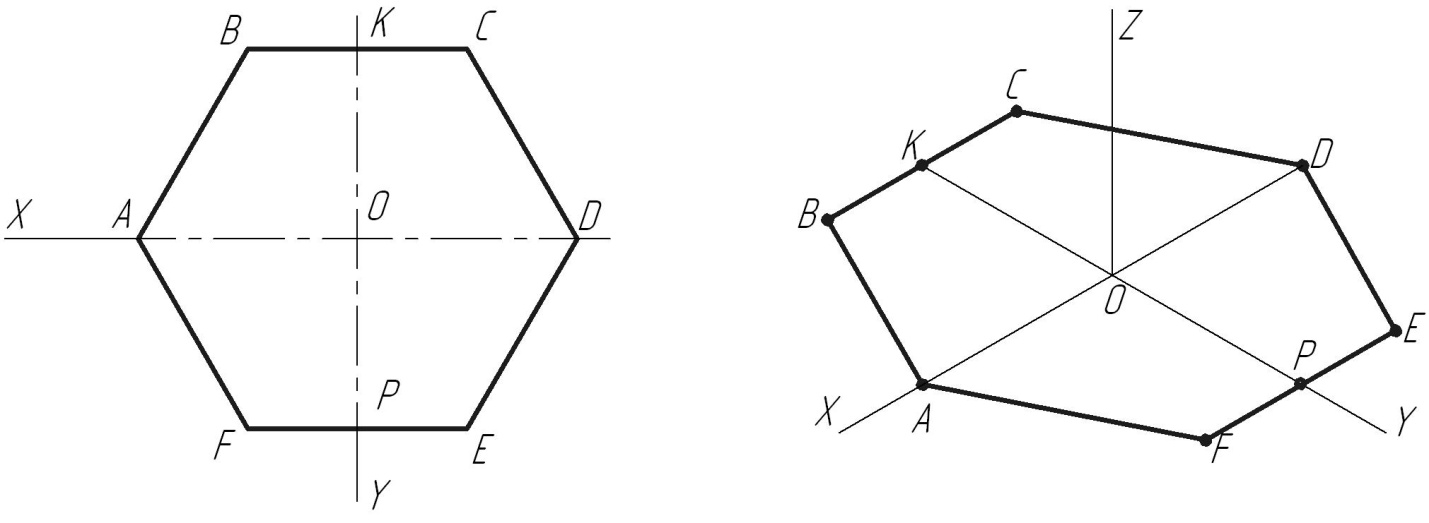
Рис. 3. Изометрическая проекция шестиугольника на чертеже
и в горизонтальной плоскости проекции
На рис. 4 представлены проекции наиболее распространенных плоских фигур в различных плоскостях проекций.
Наиболее распространённой фигурой является окружность. Изометрическая проекция окружности в общем случае представляет собой эллипс. Эллипс строят по точкам и обводят по лекалу, что в практике черчения весьма неудобно. Поэтому эллипсы заменяют овалами.
На рис. 5 построен в изометрии куб с окружностями, вписанными в каждую грань куба. При изометрических построениях важно правильно расположить оси овалов в зависимости от плоскости, в которой предполагается изобразить окружность. Как видно на рис. 5 большие оси овалов располагаются по большей диагонали ромбов, в которые спроецировались грани куба.
|
|
|
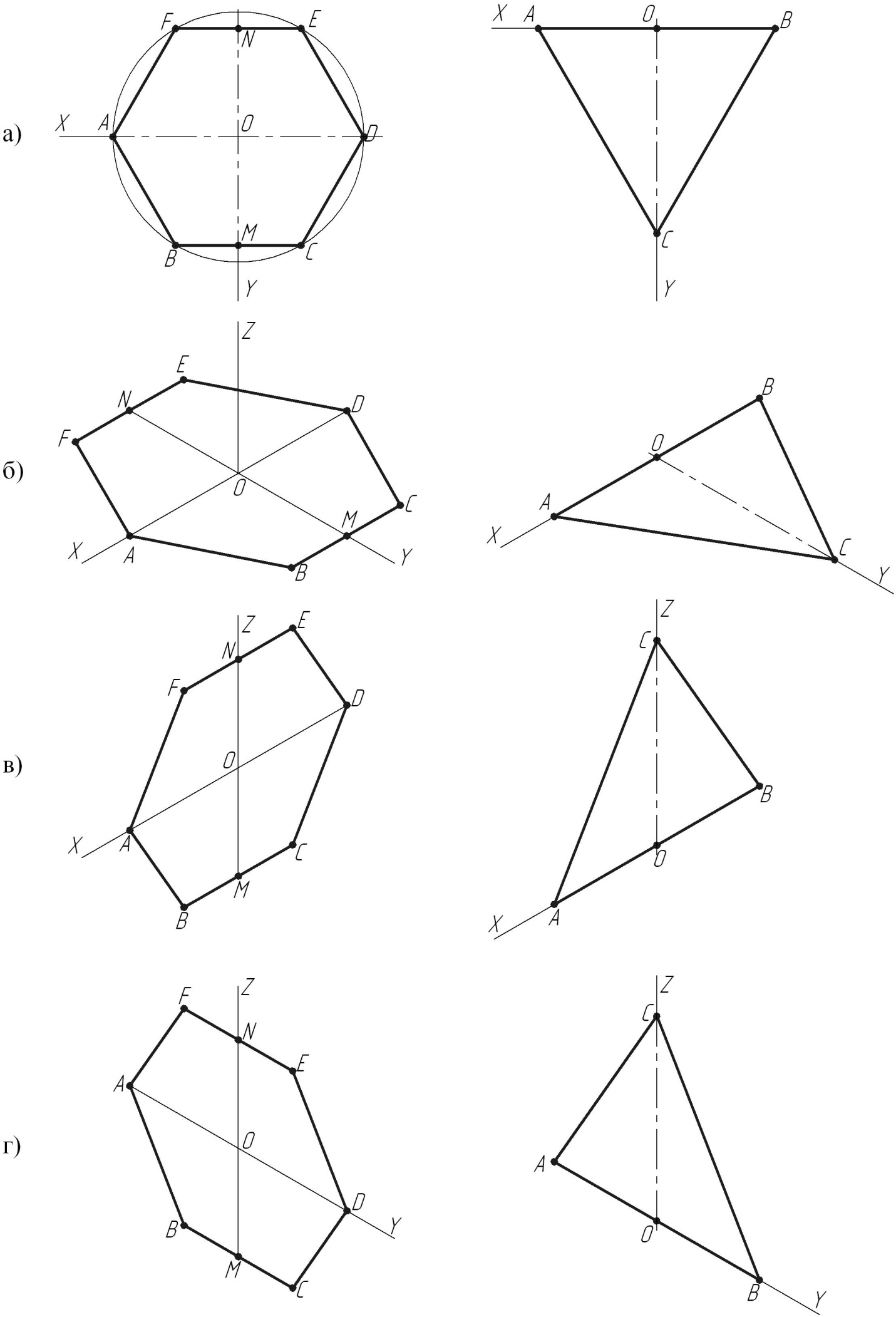
Рис. 4 Изометрическое изображение плоских фигур
а) на чертеже; б) на плоскости Н; в) на плоскости V; г) на плоскости W.
Для прямоугольной аксонометрии любого вида правило определения главных осей эллипса овала, в который проецируется окружность, лежащая в какой-либо плоскости проекции, может быть сформулировано следующим образом: большая ось овала располагается перпендикулярно к той аксонометрической оси, которая отсутствует в данной плоскости, а малая совпадает с направлением этой оси. Форма и размеры овалов в каждой плоскости изометрических проекций одинаковы.
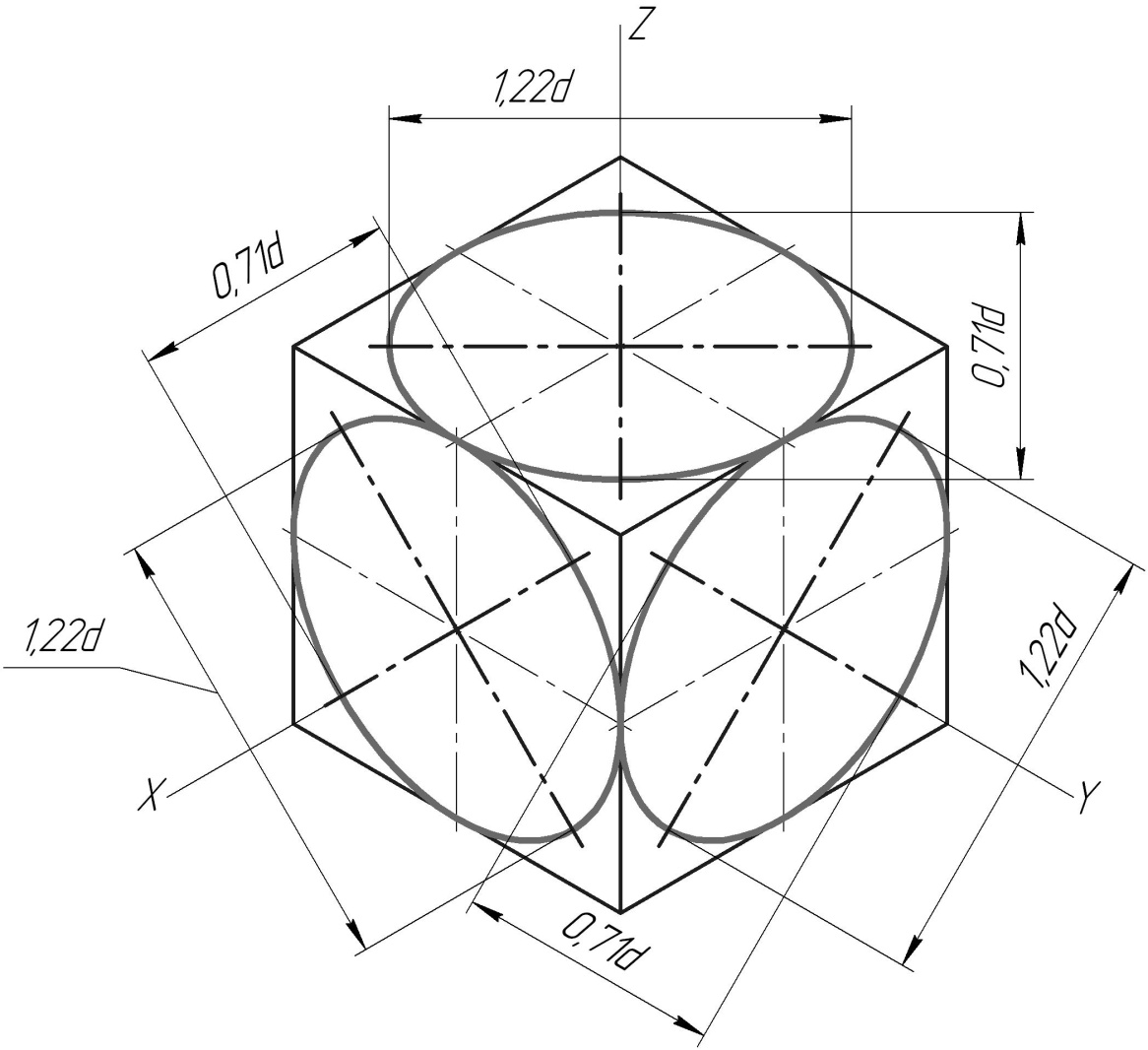
Рис. 5
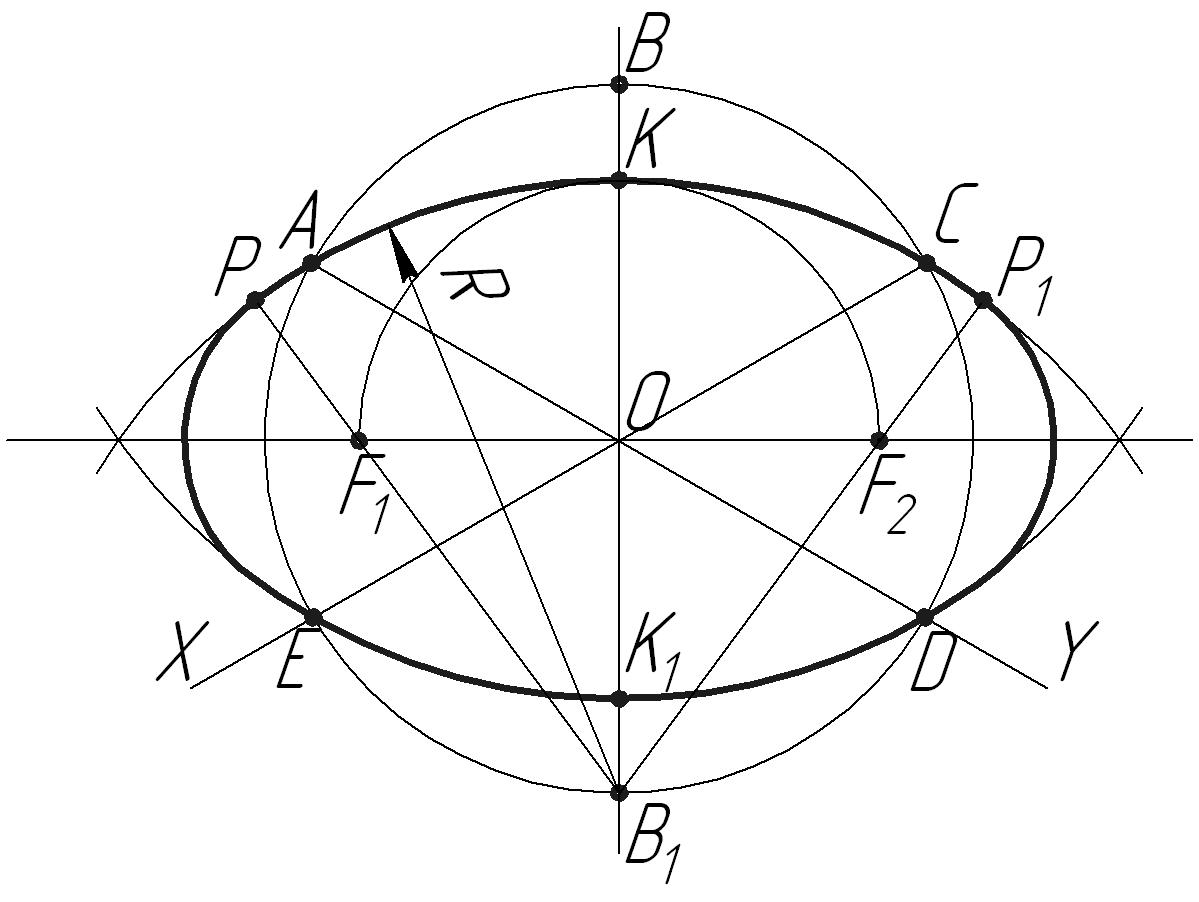
Рис. 6
Способ построения овалов в изометрии.
На рис. 6 дан пример построения проекции окружности - овала, плоскость которой параллельно плоскости H (П1).
а) Строим изометрические оси X, Y и направление осей эллипса овала (рис. 7). Направление осей эллипса показано на рис. 5.
б) Из точки Опроводим окружность заданного размера;
в) Отмечаем точки пересечения изометрических осей и осей эллипса с проведённой окружностью: A,B,C,D,B1,E.
|
|
|
г) Из точек В и В1 (точки пересечения малой оси эллипса с окружностью) проводим дуги окружности радиусом ВD и В1А. Точки пресечения этих дуг с малой осью эллипса обозначим К и К1.
д) Проводим дуги окружности радиусом ОК и отмечаем точки F1 и F2 на большой оси эллипса.
е) Соединяем точки В1F1 и В1F2. Отмечаем точки Р и Р1 (точки пересечения прямых В1F1 и В1F2 с большими дугами овала). Отрезок F1Р = F2Р1 является малым радиусом овала.
ж) Проводим дуги окружностей радиусами F1Р и F2Р1.
Полученное изображение овала принимаем за проекцию окружности на аксонометрической плоскости, у которого большая ось эллипса равна 1.22d, а длина малой оси эллипса – 0,71d: где d – заданный диаметр окружности. Если плоскость окружности параллельна плоскости проекций V или W, то построения аналогичны (рис. 6), направление же осей эллипса показано ранее (рис. 5).
Построение изометрической проекции многогранника
На рис. 7, а задана призма в ортогональных проекциях. Требуется построить изометрию данной призмы. Приведённое построение выполняется в 4 этапа.
Первый этап. Строим наружные очертания призмы рис. 7, б. Для этого проводим изометрические оси и наносим на осях Х и Y вершины углов верхнего и нижнего оснований. Для нахождения вершин углов, расположенных на оси Х, откладываем размер 58 мм (по 29 мм по обе стороны от центра О).
|
|
|
Аналогично этому для нахождения вершин углов, расположенных на оси Y, откладываем размер 46 мм (по 23 мм). Найденные таким образом точки вершин соединяем прямыми.
Второй этап. Намечаем на верхнем основании призмы и внутри её линии выреза шириной 30 мм. Определяем глубину выреза, для чего, из концов линий выреза на верхнем основании проводим вертикальные прямые и на них откладываем равный глубине выреза отрезок длиной 17 мм. Полученные точки соединяем между собой (рис. 7, в).
Третий этап. Удаляем ненужные линии (рис. 7, г)
Четвёртый этап. Обводим чертёж сплошными толстыми линиями (рис. 7, д).
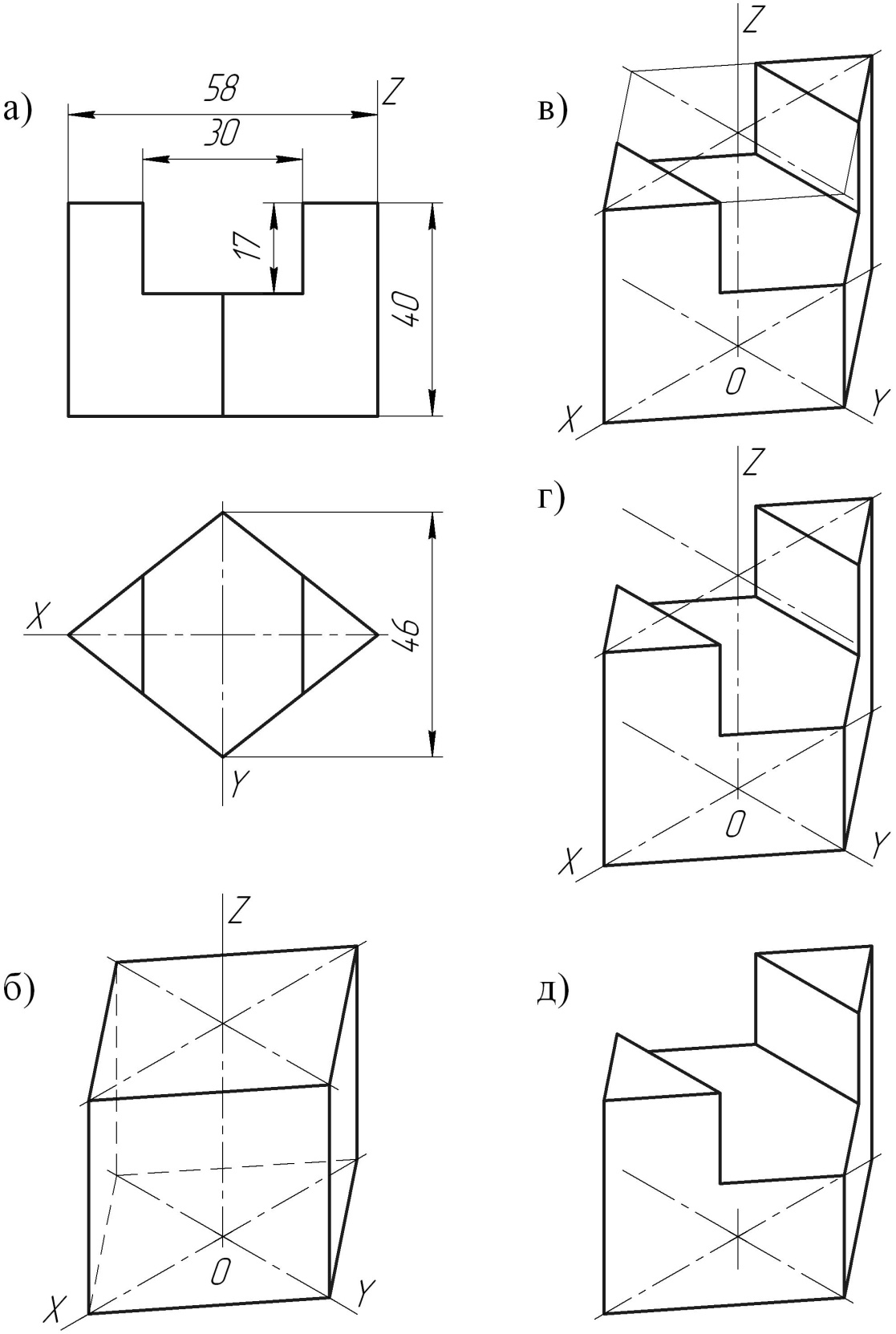
Рис. 7 Построение изометрической проекции многогранника
Домашнее задание: Начертить изометрию детали Рис.5
Ответить на вопросы для самоконтроля письменно в тетради:
1. Какую форму принимает окружность в аксонометрических изображениях?
2. Правила нанесения линий штриховки в разрезах аксонометрических изображений.
3. Расположение осей эллипсов в изометрии и диметрии при различном расположении плоскости окружности относительно плоскостей проекций.
|
|
|
Дата добавления: 2020-11-15; просмотров: 883; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
