Опыт № 3: стрельба по мишени (известна вероятность попадания)
Классическое определение вероятности
При решении задач по данной теме 89% ошибок допускается из-за невнимательного чтения условия и вычислительных ошибок, а чуть меньше 10% - из-за неверного выбора формулы решения.
Повторим сначала необходимую для решения теорию
Определение: Вероятность – доля успеха того или иного события.
Классическое определение вероятности:
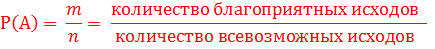
Задание №1: бросание игральной кости
Задача 1. В случайном эксперименте бросают игральную кость (кубик). Найдите вероятность того, что
1) выпадет 6 очков;
2)выпадет четное число очков;
3) выпадет 6 очков;
4) выпадет 6 очков.
Решение:
Кубик имеет шесть граней, выпадение каждой грани равнозначно, то есть всевозможные исходы это {1; 2; 3; 4; 5; 6}, тогда n =6. Рассмотрим следующие события:
A – выпадение 6-х очков
B – выпадение четного числа очков
C – выпадение менее 7-ми очков
D – выпадение 8-ми очков
Найдем вероятности событий:
А – случайное событие
Шесть очков есть только на одной грани, а потому m= 1, точнее {6}, так как граней шесть то n = 6, так как {1; 2; 3; 4; 5; 6}
0<P(A)<1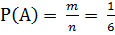 
Ответ: 
В – случайное событие
Четные числа, это {2, 4, 6}, потому m = 3, так как граней шесть то n = 6, так как {1; 2; 3; 4; 5; 6}
0<P(В)<1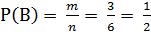 
Ответ: 0,5
C – достоверное событие
m = {1; 2; 3; 4; 5; 6} и n = {1; 2; 3; 4; 5; 6}
P(С)=1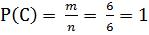 
Ответ: 1
D – невозможное событие P(D)=0
Ответ: 0.
Задание № 2: выбор трехзначного числа
Задание 2. Коля записал на доске трехзначное число. Найдите вероятность того, что записанное Колей число
|
|
|
1) делится на 5;
2) делится на 24.
Решение:
Найдем количество трехзначных чисел. Это можно сделать несколькими способами.
Способ 1. Самое большое трехзначное число 999, самое большое двузначное число 99, тогда всего трехзначных чисел 999 – 99 = 900.
Способ 2. Для записи трехзначного числа цифры записывают на трех позициях. На первом месте не может стоять «0, то есть всего 9 цифр, для оставшихся позиций таких ограничений нет, поэтому 9∙10× 10=900.
Итак, количество исходов 900: {100; 101; …; 998; 999} n =900
События: A – выбранное трехзначное число делится на 5
Найдем количество трехзначных чисел, кратных 5. Согласно признаку деления на 5: число делится на 5, если оно заканчивается на цифры 5 и 0. Для записи трехзначного числа цифры записывают на трех позициях. На первом месте не может стоять «0, то есть всего 9 цифр, для второй позиций таких ограничений нет, то есть 10, на третьей позиции всего 2 варианта, поэтому 9∙10× 2 = 180.
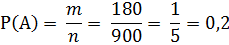
B – выбранное трехзначное число делится на 24
Найдем количество чисел, кратных 24.
100 £ 24k £999, k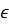 
Z Þ 
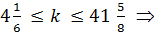k = 41 – 4 = 37
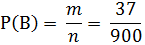
Сложение и умножение вероятностей
Теорема 1. Вероятность суммы двух несовместных событий A и B равна
|
|
|
сумме вероятностей этих событий:
P(A+B)=P(A)+P(B).
Теорема 2. Для независимых событий справедливо:
P(AB)=P(A) P(B) .
Произведением событий A и B называется событие AB, состоящее в том,
что происходят оба этих события.
Два события называются независимыми, если наступление одного из них
не влияет на вероятность наступления другого.
Опыт № 3: стрельба по мишени (известна вероятность попадания)
Задача 3. Стрелок стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что:
1) стрелок выстрелил и попал;
2) стрелок попал с третьего выстрела: два раза не попал (промахнулся), а потом в третий раз попал
3) стрелок из четырех выстрелов не попал ни разу
Решение:
Вероятность попадания при одном выстреле: P=0,7. События:
A – стрелок выстрелил и попал
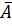– стрелок выстрелил и не попал (промахнулся)
B – стрелок три раза выстрелил: в первый раз попал, а потом два раза не попал (промахнулся)
С – стрелок из четырех выстрелов не попал ни разу
Найдем вероятности событий:
P(A) = 0,7
события A и 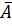– противоположные, потому P(A) + P( 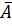) = 1, тогда
P( 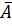) = 1 - P(A) = 1 - 0,7 = 0,3
каждое попадание/промах – независимое событие, потому
|
|
|
P(B) = P(A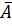)∙P( ) ∙P( 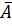) = 0,7∙0,3 ∙0,3 = 0,063
каждый промах – независимое событие
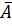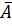P(C) = P( ) ∙P( 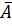)∙P( ) ∙P( )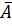
Задача 4. Научная конференция проводится в 3 дня. Всего запланировано 70 докладов: в первый день 28 докладов, остальные распределены поровну между вторым и третьим днями. На конференции планируется доклад профессора М. Порядок докладов определяется жеребьёвкой. Какова вероятность того, что доклад профессора М. окажется запланированным на последний день конференции?
Решение: Научная конференция проводится в 3 дня. Всего запланировано 70 докладов (n =70) : первый день 28 докладов, на последние два дня планируется 70 - 28 = 42 доклада. Поэтому на последний день запланировано 21 доклад m= 21. Значит, вероятность того, что доклад профессора М. окажется запланированным на последний день конференции
Задачи для самостоятельного решения
Вашему вниманию предлагаю ряд задач:
более простые https://forms.gle/MRQFr5ZD9oGBGdXY7
чуть более сложные https://forms.gle/xY8ttNTZyR11NyVXA
Для тренировки внимания, предлагаю вам проверить свои силы при выполнении заданий на внимание. Для этого просмотрите презентацию «Внимание! Внимание! Внимание! ЧАСТЬ 2»
Дата добавления: 2020-11-15; просмотров: 207; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!