Плоское напряженное состояние

НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ

Понятие о напряжениях, связь с внутренними усилиями

В брусе

 

Основываясь на модели сплошного тела, можно считать, что внутренние силы непрерывно распределены по всему сечению. Мерой внутреннего силового поля является напряжение. Есть два представления о напряжениях: среднее напряжение на данной площадке и истинное напряжение в данной точке.

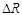Выделим в сечении С в окрестности точки К элементарную площадку . Равнодействующую внутренних сил на этой площадке обозначим . Отношение

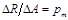
выражает среднее напряжение на данной площадке. Уменьшая размеры площадки, в пределе получим

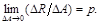
Векторная величина р есть истинное напряжение в точке К в сечении С. Напряжения, как и поверхностная нагрузка, выражаются в Н/м² (Па).

Полагая, что R − непрерывная функция А, получаем

Если R зависит от одной переменной А, то

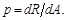
Напряжение p можно разложить на две составляющие: а) по нормали v к плоскости сечения – нормальное напряжение σ_v; б) в плоскости сечения – касательное напряжение τ_v. Такое разложение представляет практический интерес, поскольку опыты обнаруживают два характерных вида разрушения материала: вследствие отрыва частиц материала друг от друга (разрыв) и вследствие сдвига частиц материала по сечению (срез).

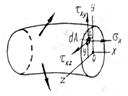Внутренние усилия в брусе находятся в тесной связи с составляющими напряжений. При выбранной в п.2.1 системе координат нормальное напряжение обозначим σ_x, а вместо одного касательного напряжения покажем два: τ_xy – параллельное оси у, τ_xz – параллельное оси z (рис.4.1).                                                           

Первый индекс в обозначении касательного напряжения (х) указывает, что оно действует на площадке, перпендикулярной оси х; второй индекс указывает, какой оси параллельно напряжение. Нормальное напряжение считают положительным если            Рис.4.1

его направление совпадает с направлением внешней нормали к плоскости         сечения. Касательное напряжение на этой площадке считают положительным,

если его направление совпадает с направлением соответствующей оси коорди-нат.

Суммируя проекции элементарных сил 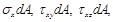a также их моменты относительно осей Ох, О y, О z получаем

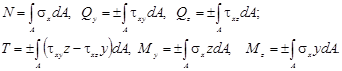
Правила знаков внутренних усилий установлены независимо от направления координатных осей, знаки же напряжений связаны с этими осями. Это приводит к необходимости согласования знаков в отдельных уравнениях, выражающих связь внутренних усилий и напряжений.

Интегральные формулы позволяют определить внутренние усилия через напряжения, если установлены законы распределения последних по сечению. Поскольку эти законы зависят от вида деформации, то обратная задача (определение напряжений через внутренние усилия) решается путем совместного использования условий равновесия и условий деформирования тела. Задача становится статически неопределимой.

В общем случае напряженное состояние в точке – состояние тела в окрестности этой точки, определяемое совокупностью всех напряжений, действующих на все элементарные площадки, содержащие рассматриваемую точку.

В дифференциальные уравнения равновесия бесконечно малого прямоугольного параллелепипеда входят шесть независимых скалярных величин, соответствующих составляющим напряжений по его граням. Они определяют тензор напряжений:

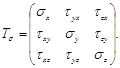
При этом учитывается свойство парности касательных напряжений (τ_xy = τ_yx, τ_xz = τ_zx, τ_yz= τ_zy): на двух взаимно перпендикулярных площадках составляющие касательных напряжений, перпендикулярные к линии пересечения площадок, равны по величине и взаимно направлены либо к линии пересечения, либо от нее.

Если площадка dA совпадает с поверхностью тела, то составляющие напряжения трансформируются в составляющие внешних сил, действующих на

 

 

поверхности тела. Соответствующие уравнения выражают условия на поверх-ности, или статические граничные условия.

Площадка, на которой касательные напряжения равны нулю, называется главной. Через точку проходят три главные площадки. По ним действуют главные напряжения, которые обозначаются σ₁, σ₂, σ₃        (σ₁ ≥ σ₂ ≥ σ₃).

 

Плоское напряженное состояние

В общем случае при переходе из одной точки в другую глав­ные напряжения изменяются непрерывно по величине и направле­нию. Случай, когда одно из главных напряжений становится равным нулю, называют плоским (двухосным) напряженным состоянием в точке. В соседних точках тела напряженное состояние может быть пространственным (трехосным).

Встречаются и такие случаи, когда во всех точках тела нап­ряженное состояние плоское и при этом площадки с нулевым глав­ным напряжением параллельны друг другу. В таком случае все те­ло испытывает плоское напряженное состояние. Примером может служить пластинка, подверженная воздействию поверхностной и (или) объемной нагрузки, распределенной равномерно по толщине. При этом равны нулю главные напряжения на площадках в плоскости пластинки, а два других отличны от нуля и, вообще говоря, изменяются при переходе из одной точки в другую.

Три независимые скалярные величины, соответствующие составляющим напряжений, определяют тензор напряжений:

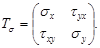
Для определения главных напряжений представляет интерес исследование напряжений, действующих лишь на площадках, перпендикулярных к главной площадке с нулевым глав­ным напряжением. Рассмотрим прямую призму с основанием ВС D высотой dz (рис.4.2).

Уравнения равновесия запишем в виде проекции сил на нап­равления σ_α и τ_α: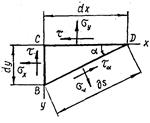

σ_α dzds – (σ_y dzds cosα) cosα– (τ dzds cosα)sinα –– (σ_x dzds sinα) sinα – (τ dzds sinα) cosα = 0,

τ_α dzds + (σ_y dzds cosα) sinα – (τdzds cosα) cosα –– (σ_x dzds sinα) cosα + (τdzds sinα) sinα= 0.

После сокращения на dzds и преобразо-вания получим

σ_α = σ_xsin²α + σ_ycos²α+τsin2α;                 

          τ_α= 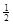(σ_x – σ_y)sin2α+ τcos2α.                               Рис. 4.2

Чтобы определить положение главных площадок, следует либо приравнять нулю производную dσ_α/ dα, либо положить равными нулю касательные напряжения τ_α ввиду их отсутствия на главных пло­щадках. В обоих случаях

получаем следующее уравнение для угла наклона главных площадок (α₀):

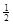(σ_x – σ_y) sin2α₀+ τcos2α₀ = 0 ,

откуда

tg2α₀= 2τ /(σ_у– σ_х) ,

чему соответствуют углы α₀′ и α₀′+ 90°, которые определяют две взаимно перпендикулярные площадки.

Исследуя вторую производную d ²σ_α/ dα², можно убедиться, что на главной площадке под углом α₀′ при σ_y >σ_x действует мак­симальное главное напряжение σ₁ ,а на площадке под углом α₀′+ 90° действует минимальное главное напряжение σ₂.

Для определения главных (экстремальных нормальных) нап­ряжений отразим значение угла α₀ в выражении σ_α, используя при этом формулы для sin2α₀, соs2α₀, соs²α₀, sin²α₀, приведенные в п.3.4. В итоге

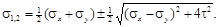
Если одно из напряжений σ _x или σ _y равно нулю, то формула примет вид

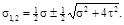
Экстремальные касательные напряжения можно выразить через главные напряжения: ± 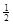( σ₁− σ₂), что соответствует выражению

Они действуют на площад­ках, наклоненных к главным под углом 45° и направлены от σ_min к σ_max (рис.4.3). В общем случае на этих площадках σ_α ≠ 0.

Если оси х и у совмещены с главными осями 1 и 2, то

σ_α = σ₁sin²α + σ₂cos²α ;

τ_α= 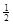(σ₁ − σ₂)sin2α.

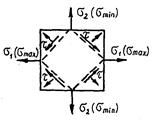При α = 45° и σ₂ = −σ₁ = −σ имеем τ_α = σ, σ_α = 0. Такое напряженное состояние называется чистым сдвигом, а площадки – площадками чистого сдви-га.

В случае σ₁ = σ₂ = σ на всех площадках, проходящих через исследуемую точку, τ_α = 0, σ_α = σ. Такое напряженное состояние называется равномерным двухосным растяжением (или сжатием).                                                                                    Рис. 4.3

При одноосном напряженном состоянии (σ₂ =  σ₃ = 0) имеем

σ_α = σ₁sin²α;                  τ_α= 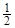σ₁sin2α.

Экстремальные касательные напряжения равны ± σ₁ /2.

Перемещения и деформации

Твердое тело, как правило, закреплено. В таком случае пе­ремещение точки тела вызывается только его деформированием. Это перемещение характеризуется вектором 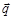 с проекциями u , v , w на оси x , у, z , являющимися функциями координат: u = u(x , у, z), v = v(x , у, z), w = w(x , у, z). В силу сплошности тела эти функции и их частные производные требуемого порядка по x , у, z непрерывны, кроме, возможно, особых точек, линий или поверхно­стей.

Элементарный параллелепипед, вырезанный в окрестности ка­кой-либо точки, деформируется таким образом, что изменяется длина его ребер и искажаются первоначально прямые углы между гранями, т.е. изменяются объем и форма.

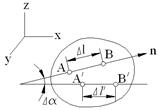Для определения линейной деформации в точке А вдоль оси n (рис.4.4) возьмем в теле на этой оси малый отрезок АВ длиной ∆l . После деформирования те­ла он обратится в отрезок А'В', составляющий с отрезком АВ угол ∆α, и будет иметь длину ∆l '. Исходя из незначи­тельного изменения геометри­ческих характеристик тела в результате деформирования, можно считать                                       Рис. 4.4

 угловое пере­мещение (угол поворота) ∆α малым по сравнению с единицей, так что cos∆α ≈ 1. Величина ∆λ = ∆l ' – ∆l представляет со­бой абсолютное изменение первоначальной длины отрезка АВ. Ве­личина ∆λ/∆l есть средняя линейная деформация вдоль оси n в точке А.

Уменьшая размеры отрезка, в пределе получаем

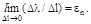
Безразмерная величина ε_n есть истинная линейная деформация вдоль оси n в точке А.

Полагая, что λ − непрерывная функция l, получим

ε_n = ∂ λ /∂l.

Если λ зависит от одной переменной l, то

ε_n = dλ /dl.

Для определения деформации сдвига в точке А в плоскости mn возьмем на этой плоскости два малых отрезка АВ и АС, пересекающихся в точке А под углом 90°. После деформирования тела они обратятся в отрезки А'В' и А'С' с

 

иным углом пересечения и расположатся в другой плоскости m ' n ', составляющей с первоначальной угол ∆α. Принимая, как и раньше, cos∆α ≈ 1, определим деформацию сдвига как разность величин углов В'А'С' и ВАС. Наложим угол В'А'С' на угол ВАС (рис.4.5) и установим углы поворота отрезков относительно своих первоначальных положений – α₁ и α₂. Величина α₁ + α₂ = γ_mn и есть деформация сдвига в точке А в плоскости mn.

Положительными принимают линей­ную деформа-цию, соответствующую растяжению, и деформацию сдвига, отвечающую уменьшению первона­чального угла пересечения отрезков.

Полагая деформации малыми, мы можем в дальнейшем пренебрегать ими по сравнению с едини-цей, а также их высокими сте­пенями по сравнению с первой степенью.

 Рис. 4.5                Деформированное состояние в точке – состояние тела в ок­рестности данной точки, определяемое совокупностью деформаций всех линейных элементов, проходящих через данную точку. В слу­чае малых деформаций оно полностью определяется линейными де­формациями трех взаимно перпендикулярных линейных элементов тела, проходящих через данную точку, и тремя деформациями сдвига этих линейных элементов. Соответствующие шесть незави­симых скалярных величин определяют тензор деформаций:

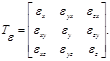
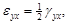
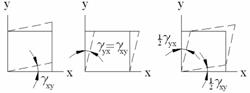
Здесь  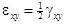(при γ_yx=γ_xy),…Последнее оправдывается идентичностью трех ситуаций для грани деформированно­го параллелепипе-да, что видно, например, из рис. 4.6 (в плоско­сти xy).

Рис. 4.6

Главные оси деформации – три взаимно перпендикулярные прямые, прохо-дящие через данную точку тела и совпадающие по направлениям с такими тре-мялинейными элементами тела, которые остаются взаимно перпендикулярны-ми и после деформации. Линейные деформации по направлениям этих осей на-

 

зываются главными деформациями и обозначаются ε₁, ε₂, ε₃ (ε₁ ≥ ε₂ ≥ ε₃).

Кинематические граничные условия на части поверхности тела с заданным вектором перемещений 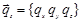имеют вид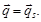

---

Дата добавления: 2020-11-15; просмотров: 72; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!