Представим результаты расчета в табличной форме.
Теоретическая часть
Стержневая геометрически неизменяемая система после условной замены ее жестких узлов шарнирами называется ФЕРМОЙ. Узел фермы – это место соединения ее элементов (стержней). В узле могут соединяться два или более двух стержней (три, четыре…).
Если нагрузки, действующие на ферму, приложены в узлах, стержни фермы работают на осевое растяжение-сжатие.
Разработан целый ряд аналитических и графических методов определения внутренних усилий в элементах статически определимых и статически неопределимых ферм, подробно эти методы изучаются в курсе «Строительная механика», в данном примере рассматриваются два из них: метод вырезания узлов и метод моментной точки (способ Риттера).
Метод вырезания узлов
этот метод состоит в том, что от фермы мысленно отсекается узел, в местах разрезов стержней прикладываются действующие в них внутренние усилия, а затем составляются уравнения равновесия вырезанного узла. Так как для плоской системы сходящихся сил можно записать только два независимых уравнения равновесия, обычно их представляют в виде суммы проекций сил на две непараллельные оси. В качестве таких осей удобно выбирать оси, перпендикулярные направлениям внутренних усилий.
Стержни, в которых не действуют внутренние растягивающие или сжимающие силы называются нулевыми.
Выявить наличие в ферме нулевых стержней и упростить решения уравнений равновесия позволяют некоторые частные случаи определения усилий в вырезанных узлах:
1. В ненагруженном двухстержневом узле оба стержня нулевые (N 1 =0; N 2 =0).
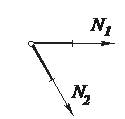
2. Если в ненагруженном трехстержневом узле два стержня лежат на одной прямой, усилия в этих стержнях равны между собой (N1= N2), а усилие в третьем стержне равно нулю (N3= 0).
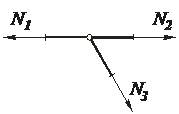
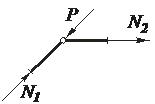
3. Если к узлу фермы, в котором сходятся два стержня, не лежащие на одной прямой, приложена внешняя сила Р, направленная по оси одного из стержней, то внутреннее усилие в этом стержне равно по модулю величине приложенной силы, но противоположно ей направлено (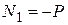 
). Усилие во втором стержне равно нулю (стержень нулевой, 
).
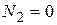4. Если в узле фермы сходятся три стержня, два из которых лежат на одной прямой, а внешняя сила направлена вдоль оси третьего стержня, то внутреннее усилие в этом стержне равно по модулю величине приложенной силы, но противоположно ей направлено (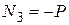 
), усилия в других стержнях одинаковы (N1= N2).
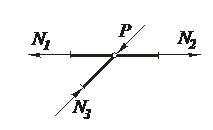
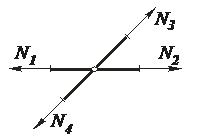
5. Если в ненагруженном четырехстержневом узле оси стержней направлены по двум прямым, то N1= N2 и N3= N4.
Метод моментной точки (способ Риттера)
Рассматриваемый метод заключается в том, что ферма рассекается на две части, в местах разреза стержней прикладываются внутренние усилия (обычно их считают растягивающими). Затем составляется условие равенства нулю моментов всех внутренних и внешних сил относительно точки пересечения осей всех рассеченных стержней за исключением стержня, в котором определяется усилие. Эта точка называется моментной, или точкой Риттера.
Например, для определения усилия в первом стержне фермы, реакции опор которой направлены вверх и равны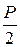 
, рассечем ферму на две части таким образом, чтобы из уравнения 
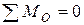(сумма моментов относительно моментной точки О)можно было определить искомое усилие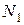 
.
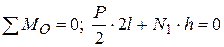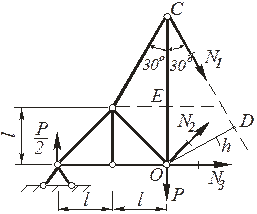
Из прямоугольного треугольника OCD находим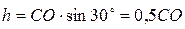 
.
Очевидно (рис. 1.42), что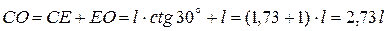 
.
Тогда
.
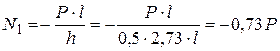Определив усилия во всех стержнях фермы первым или вторым способом, переходят к подбору площадей их поперечных сечений, а поскольку в рассматриваемой задаче все стержни имеют одинаковую площадь поперечного сечения, расчет ведется для стержня, в котором действует максимальное по модулю внутреннее усилие.
Из условия прочности этого стержня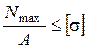 
следует, что требуемая площадь его поперечного сечения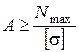 
.
Пример решения задачи.
ЗАДАЧА
Задание :
1) определить усилия в стержнях;
2) из условия прочности растянутых стержней определить величину площади сечения A этих стержней, если заданы предел текучести материала стержней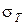 
= 300 МПа и запас прочности по отношению к пределу текучести 
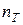=1,5.
Силы, приложенные в узлах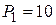 
кН и 
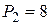кН.
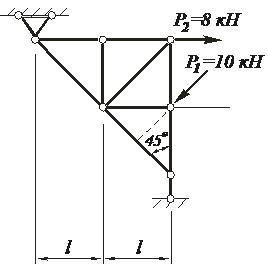
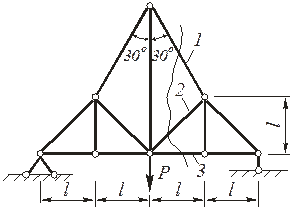
Рисунок 1 – Заданная расчетная схема
Решение.
1. Определение внутренних усилий в стержнях фермы.
1.1. Для удобства расчета пронумеруем стержни фермы и обозначим узлы фермы буквами A, B, C, D, E, G . Вертикальные реакции опор А и В обозначим соответственно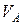 
и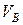 
. Горизонтальная реакция опоры А обозначена 
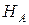(рисунок 2, б).
1.2. Для определения опорной реакции 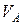составим уравнение
: 
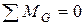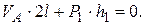
Учитывая, что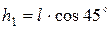 
, имеем
,
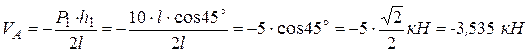отрицательный результат расчета показывает, что опорная реакция направлена не вверх, а вниз.
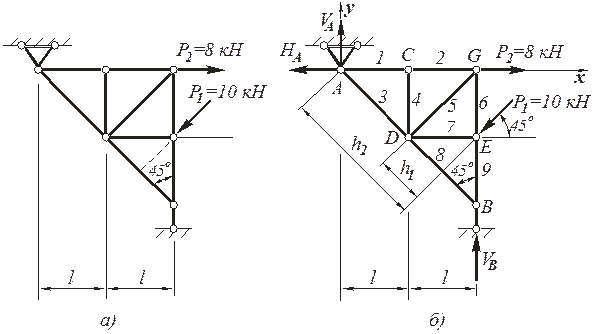
а) заданная схема фермы,
б) расчетная схема к определению внутренних усилий
Рисунок 2 - К примеру решения задачи 2
1.3. Определяем реакцию :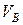
; 
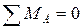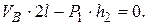
Плечо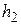 
силы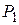 
относительно точки А найдем из расчетной схемы фермы
.
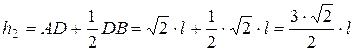Тогда
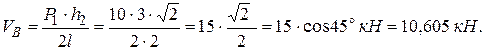
1.4. Определим горизонтальную реакцию опоры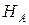 
, составив уравнение 
.
.
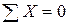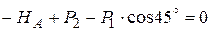Отсюда
.
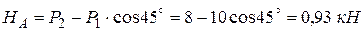1.5. Вычислив сумму проекций сил, приложенных к ферме на ось y, проверим правильность определения вертикальных опорных реакций
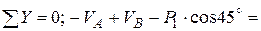
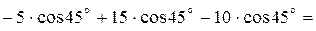
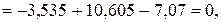
реакции опор вычислены верно.
1.6. Вычисляем внутренние усилия в стержнях фермы.
Вырезаем узел А, в котором сходятся два стержня (рисунок 3, а) и составляем уравнения его равновесия
.
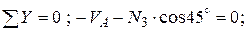
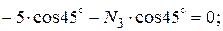
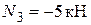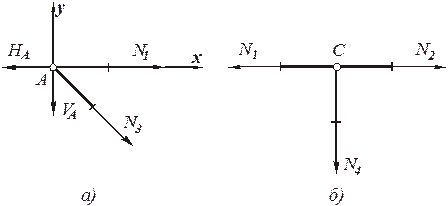
а) узел А, б) узел С
Рисунок 3 - Схемы вырезания узлов А и С
Усилие в третьем стержне сжимающее. Учитывая, что вектор N3 направлен к узлу, имеем
;
.
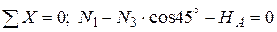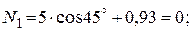
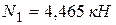Вырезаем ненагруженный узел С, в котором сходятся три стержня (рисунок 3, б), два из которых (стержни АС и СО) лежат на одной прямой, следовательно,
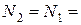4,465 кН, а 
.
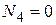Вырезав узел G (рис. 1.45, а) и проведя оси u, x, составляем условия равновесия узла.
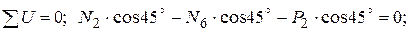
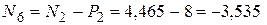кН,
шестой стержень сжат;
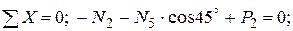
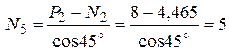кН.
Вырезаем узел Е, в котором сходятся три стержня (рисунок 4, б) и записываем два условия равновесия
;
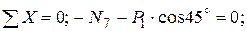
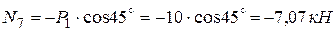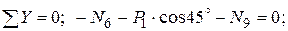
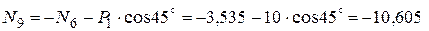кН.
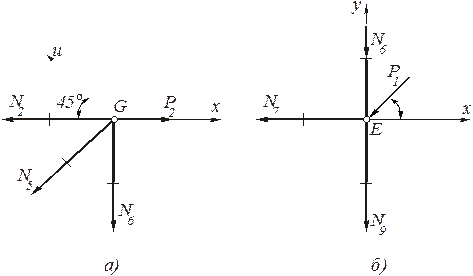
а – узел G, б – узел Е
Рисунок 4 - Схемы вырезания узлов G и Е
В двухстержневом узле В внутреннее усилие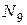 
равно опорной реакции 
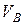, сжимающей девятый стержень
,
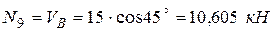что совпадает с ранее полученным результатом. Восьмой стержень является нулевым.
Представим результаты расчета в табличной форме.
| ВНУТРЕННИЕ УСИЛИЯ В СТЕРЖНЯХ ФЕРМЫ, кН | ||||||||
| N1 | N2 | N3 | N4 | N5 | N6 | N7 | N8 | N9 |
| 4,47 | 4,47 | -5 | 0 | 5 | -3,54 | -7,07 | 0 | -10,61 |
Примечание: в таблице приведены величины внутренних усилий в стержнях.
2. Определение площадей поперечных сечений растянутых стержней.
2.1. Определяем площадь поперечного сечения пятого стержня. Наибольшее растягивающее усилие возникает в пятом стержне: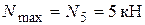 
.
Условие прочности пятого стержня запишется в виде:
.
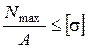Учитывая, что допускаемое напряжение материала стержня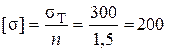 
МПа, имеем
.
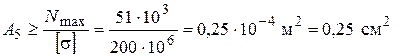2.2. Площади поперечных сечений сжатых стержней подбираются из условия устойчивости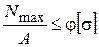 
.
Дата добавления: 2020-11-15; просмотров: 130; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!