Задачи для самостоятельного решения.
Практическое занятие №1.
Тема: Применение производных к исследованию функций и построению графиков.
Форма проведения – решение задач под руководством преподавателя или с использованием рабочих тетрадей, содержащих разобранные примеры и задачи для самостоятельного решения.
Время проведения занятия – 4 час.
Занятие проводится аудиторно (традиционная технология) или с использованием сети Интернет в режиме of-line – электронная почта, форум.
Вопросы по задачам для самостоятельного решения обсуждаются на форуме.
Для выполнения задания необходимо изучить теоретический материал модуля 1 для третьего семестра (лекция 1).
Если вопросов по выполнению задания нет, то решить задачи №1 - №8 из КР №1. Текст КР №1 находится в методических указаниях ко 2 семестру. Файл с решенными задачами переслать преподавателю через форум. Если задачи решены верно, то студент получает оценку «зачтено» за выполнение практического занятия 1.
Примеры решения задач
| 1. Возрастание и убывание функций | |||||||||||||||||||||||||||||||||||||||||
| №1. |  По данному графику функции По данному графику функции  постройте вид графиков постройте вид графиков  .
Решение:
1) На интервале .
Решение:
1) На интервале   убывает, убывает,  , ,  , ,  . .
 2) На интервале 2) На интервале   возрастает, возрастает,  , ,
 .
3) На интервале .
3) На интервале   убывает, убывает,  , ,  .
4) .
4)  .
5) На интервале .
5) На интервале   возрастает, возрастает,  , на интервале , на интервале   убывает, убывает,  . Эти соображения позволяют построить примерный график . Эти соображения позволяют построить примерный график 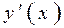 .
6) .
6) 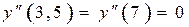
 Та же последовательность действий, примененная к графику функции Та же последовательность действий, примененная к графику функции 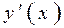 , дает примерный график второй производной , дает примерный график второй производной  . .
| ||||||||||||||||||||||||||||||||||||||||
| №2. | По данному графику производной  постройте вид графика функции постройте вид графика функции  .
Решение: .
Решение:
 1) На интервале 1) На интервале   , ,  возрастает, возрастает,  , т.е., скорость возрастания , т.е., скорость возрастания  также неограниченно возрастает, а следовательно, и сама функция также неограниченно возрастает, а следовательно, и сама функция  неограниченно возрастает, таким образом, неограниченно возрастает, таким образом, 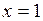 – вертикальная асимптота графика.
2) На интервале – вертикальная асимптота графика.
2) На интервале   , ,  возрастает, причем возрастает, причем  , (чем ближе точка к , (чем ближе точка к 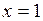 – справа от нее, тем больше скорость возрастания), что указывает, что – справа от нее, тем больше скорость возрастания), что указывает, что  , т.е., , т.е., 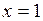 – точка разрыва второго рода.
3) В точке – точка разрыва второго рода.
3) В точке 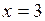 производная меняет знак с «+» на «–», производная меняет знак с «+» на «–», 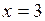 – точка локального максимума.
4) На интервале – точка локального максимума.
4) На интервале   , ,  убывает.
5) В точке убывает.
5) В точке  производная меняет знак с «–» на «+», производная меняет знак с «–» на «+»,  – точка локального минимума. – точка локального минимума.
 6) При 6) При  функция возрастает.
Эти соображения позволяют построить примерный график функция возрастает.
Эти соображения позволяют построить примерный график  : :
| ||||||||||||||||||||||||||||||||||||||||
| №3. | Функция  возрастает на интервале возрастает на интервале  , так как для , так как для   .
Полезный вывод: поскольку .
Полезный вывод: поскольку  , то , то  , значит , значит  для для  . .
| ||||||||||||||||||||||||||||||||||||||||
| № п/п | 2. Экстремумы функции | ||||||||||||||||||||||||||||||||||||||||
| №4. | Для функции  на отрезке на отрезке  значение значение  является минимальным, т.к. производная является минимальным, т.к. производная  равна нулю в точке равна нулю в точке  . .
| ||||||||||||||||||||||||||||||||||||||||
| №5. |  Функция Функция 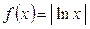 не дифференцируема в точке не дифференцируема в точке  , так как касательные к графику функции слева и справа от точки , так как касательные к графику функции слева и справа от точки 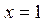 различны, однако функция имеет минимум в этой точке. Функция различны, однако функция имеет минимум в этой точке. Функция  является строго убывающей при является строго убывающей при  и строго возрастающей при и строго возрастающей при  . В точке . В точке  график имеет острый минимум (так называемую угловую точку). график имеет острый минимум (так называемую угловую точку).
| ||||||||||||||||||||||||||||||||||||||||
| №6 |  Функция Функция  и ее производная имеют бесконечный разрыв при и ее производная имеют бесконечный разрыв при  . Функция возрастает при . Функция возрастает при  и убывает при и убывает при  , но экстремума в точке , но экстремума в точке  не имеет. не имеет.
| ||||||||||||||||||||||||||||||||||||||||
| №7. |  Функция Функция 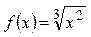 не дифференцируема в точке не дифференцируема в точке 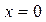 , так как , так как  при при  , график функции имеет в точке 0 вертикальную касательную, функция является убывающей при , график функции имеет в точке 0 вертикальную касательную, функция является убывающей при  , возрастающей при , возрастающей при  , в точке , в точке  функция имеет минимум (такая точка графика называется точкой возврата). функция имеет минимум (такая точка графика называется точкой возврата).
| ||||||||||||||||||||||||||||||||||||||||
| №8. |  Для функции Для функции  в точке в точке  выполняется необходимое условие экстремума выполняется необходимое условие экстремума  . Однако точка . Однако точка  не является точкой экстремума этой функции, в ней не выполняется достаточное условие экстремума, т.к. не является точкой экстремума этой функции, в ней не выполняется достаточное условие экстремума, т.к. 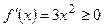 для любых для любых  и функция и функция  возрастает на всей числовой оси. возрастает на всей числовой оси.
| ||||||||||||||||||||||||||||||||||||||||
| № п/п | 3. Асимптоты графика функции | ||||||||||||||||||||||||||||||||||||||||
| №9. | У графика   существует левая горизонтальная асимптота существует левая горизонтальная асимптота  ( (  ) и не существует правой горизонтальной асимптоты. ) и не существует правой горизонтальной асимптоты.
| ||||||||||||||||||||||||||||||||||||||||
| №10 | У графика   существует правая горизонтальная асимптота существует правая горизонтальная асимптота  ( (  ) и не существует левой горизонтальной асимптоты. ) и не существует левой горизонтальной асимптоты.
| ||||||||||||||||||||||||||||||||||||||||
| №11 | У графика   существуют обе горизонтальные асимптоты: существуют обе горизонтальные асимптоты:  - левая горизонтальная асимптота ( - левая горизонтальная асимптота (  ), ),
 - правая горизонтальная асимптота ( - правая горизонтальная асимптота ( 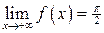 ). ).
| ||||||||||||||||||||||||||||||||||||||||
| №12 |  У графика У графика  обе горизонтальных асимптоты обе горизонтальных асимптоты  существуют и совпадают ( существуют и совпадают (  ). Кроме того, график функции ). Кроме того, график функции  имеет вертикальную асимптоту имеет вертикальную асимптоту 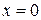 , поскольку , поскольку  , ,  . .
| ||||||||||||||||||||||||||||||||||||||||
| №13 |  Кривая Кривая  имеет вертикальные асимптоты имеет вертикальные асимптоты  и и  . .
| ||||||||||||||||||||||||||||||||||||||||
| №14 |  Построим график функции Построим график функции  без использования производной.
Преобразуем выражение: без использования производной.
Преобразуем выражение:    , ,  .
График этой функции получается смещением графика .
График этой функции получается смещением графика 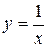 на две единицы влево, на одну единицу вверх и выкалыванием точки графика с абсциссой на две единицы влево, на одну единицу вверх и выкалыванием точки графика с абсциссой  .
Прямые .
Прямые  и и  являются вертикальной и горизонтальной асимптотами.
Для гиперболы с центром симметрии в точке являются вертикальной и горизонтальной асимптотами.
Для гиперболы с центром симметрии в точке   уравнения вертикальной и горизонтальной асимптот имеют вид: уравнения вертикальной и горизонтальной асимптот имеют вид:  и и  . .
| ||||||||||||||||||||||||||||||||||||||||
| №15 | Найдите асимптоты графика функции  . .  , ,  , ,  .
График имеет две несовпадающие наклонные асимптоты: левую .
График имеет две несовпадающие наклонные асимптоты: левую  и правую и правую  . . 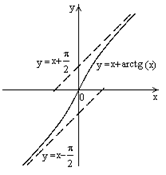
| ||||||||||||||||||||||||||||||||||||||||
| № п/п | 4. Построение графиков функций | ||||||||||||||||||||||||||||||||||||||||
| №16 | Исследуйте функцию  и постройте её график.
1). Функция определена при всех и постройте её график.
1). Функция определена при всех  . Для нахождения точек пересечения с осями записываем уравнения . Для нахождения точек пересечения с осями записываем уравнения  и и  ; получаем, что ось ; получаем, что ось  пересекается в точке с пересекается в точке с  , а ось , а ось  - в точках - в точках  и и  .
2). Точек разрыва нет. Так как нет точек разрыва 2-го рода, вертикальные асимптоты отсутствуют. Ищем параметры наклонных асимптот. .
2). Точек разрыва нет. Так как нет точек разрыва 2-го рода, вертикальные асимптоты отсутствуют. Ищем параметры наклонных асимптот.  , ,   При вычислении второго предела использовано правило Лопиталя для раскрытия неопределённости типа
При вычислении второго предела использовано правило Лопиталя для раскрытия неопределённости типа  . Итак, у графика есть наклонная асимптота; её уравнение . Итак, у графика есть наклонная асимптота; её уравнение  3). Находим производную:
3). Находим производную: 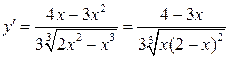 .
Знак производной определяется знаком выражения .
Знак производной определяется знаком выражения  или или  . Видим, что в области . Видим, что в области   , при , при   и при и при   . Получаем, что в области . Получаем, что в области  функция убывает, при функция убывает, при  - возрастает и при - возрастает и при  - убывает. Находим критические точки. - убывает. Находим критические точки.  при при  , ,
 не существует при не существует при  , ,  . При переходе через . При переходе через  знак производной меняется с (-) на (+), т.е. это точка минимума. При знак производной меняется с (-) на (+), т.е. это точка минимума. При  производная не существует, значит, минимум острый. производная не существует, значит, минимум острый.  При переходе через вторую критическую точку При переходе через вторую критическую точку  производная меняет знак с (+) на (-) , т.е. при производная меняет знак с (+) на (-) , т.е. при  - максимум: - максимум: 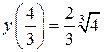 . При переходе через . При переходе через  знак производной не меняется, значит экстремума нет.
4) Находим вторую производную: знак производной не меняется, значит экстремума нет.
4) Находим вторую производную:  . Видим, что . Видим, что  при при  ; в этой области график выпуклый; ; в этой области график выпуклый;  при при 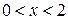 , т.е. интервал , т.е. интервал  также является областью выпуклости. При также является областью выпуклости. При   , следовательно, при , следовательно, при  график вогнут. Найдём точки перегиба. Вторая производная не существует при график вогнут. Найдём точки перегиба. Вторая производная не существует при  и при и при  . При переходе через первую точку знак . При переходе через первую точку знак  не меняется, а при переходе через вторую – меняется. Итак, точкой перегиба является точка с координатами не меняется, а при переходе через вторую – меняется. Итак, точкой перегиба является точка с координатами  , ,  . .
|
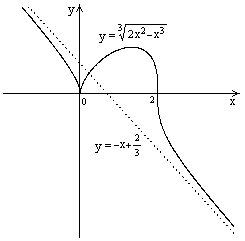 График имеет вид:
График имеет вид:
| № п/п | 8. Нахождение наибольшего и наименьшего значения непрерывной функции на отрезке | ||||||||||||||||
| №17 | Найдите наибольшее и наименьшее значения функции  на на  . .
  .
Вторая группа решений является частью первой и .
Вторая группа решений является частью первой и  . Отрезку . Отрезку  принадлежат точки принадлежат точки  и и  . Найдем значения функции в точках . Найдем значения функции в точках  , , 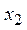 и на концах отрезка: и на концах отрезка:  , ,  , ,  , ,  .
Сравнивая их между собой, заключаем, что .
Сравнивая их между собой, заключаем, что  , ,  для для  . .
| ||||||||||||||||
| № п/п | 9. Текстовые задачи разного содержания на нахождение наибольшего и наименьшего значения величин | ||||||||||||||||
| №18 |  Площадь поверхности сферы равна Площадь поверхности сферы равна  . Какова высота цилиндра наибольшего объема, вписанного в эту сферу?
Обозначим высоту цилиндра . Какова высота цилиндра наибольшего объема, вписанного в эту сферу?
Обозначим высоту цилиндра  , , 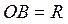 . По условию . По условию  , ,  .
Из .
Из  : : 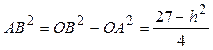 . Объем цилиндра . Объем цилиндра  . По смыслу задачи . По смыслу задачи  , т.е. , т.е.  . Исследуем функцию . Исследуем функцию  на этом интервале. Производная на этом интервале. Производная  при при  , вблизи этого значения , вблизи этого значения  меняет знак с + на –, значит при этой высоте объем цилиндра будет наибольшим. меняет знак с + на –, значит при этой высоте объем цилиндра будет наибольшим.
| ||||||||||||||||
| №19 | Владелец фабрики установил, что если он будет продавать свои изделия по цене  руб., то его годовая прибыль руб., то его годовая прибыль  составит составит  руб. Определите руб. Определите  , при котором прибыль будет максимальной. , при котором прибыль будет максимальной.
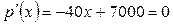 при при  , при этой цене прибыль будет максимальной. , при этой цене прибыль будет максимальной.
| ||||||||||||||||
| №20 | Требуется построить несколько одинаковых домов с общей площадью 40000 м2. Затраты на постройку одного дома, имеющего  м2 площади, складываются из стоимости наземной части, пропорциональной м2 площади, складываются из стоимости наземной части, пропорциональной  , и стоимости фундамента, пропорциональной , и стоимости фундамента, пропорциональной  . Стоимость наземной части составляет 32% стоимости фундамента для дома площадью 1600 м2. Определите, сколько нужно построить одинаковых домов, чтобы сумма затрат была наименьшей.
РЕШЕНИЕ:
Обозначим через . Стоимость наземной части составляет 32% стоимости фундамента для дома площадью 1600 м2. Определите, сколько нужно построить одинаковых домов, чтобы сумма затрат была наименьшей.
РЕШЕНИЕ:
Обозначим через  число домов, число домов,  по условию. Стоимость всей постройки по условию. Стоимость всей постройки
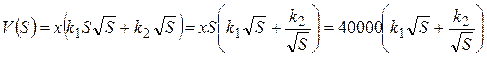 ,
где ,
где  и и 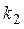 – коэффициенты пропорциональности, найдем их из условия – коэффициенты пропорциональности, найдем их из условия  при при  , значит, , значит,  и и  .
Производная .
Производная  при при  .
Исследуя знак производной, можно показать, что эта точка является точкой минимума .
Исследуя знак производной, можно показать, что эта точка является точкой минимума  . При наименьших затратах можно построить . При наименьших затратах можно построить 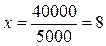 домов. домов.
| ||||||||||||||||
| №21 | Величина угла при основании равнобедренного треугольника равна 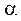 . При каком значении . При каком значении 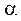 отношение длины радиуса вписанной в данный треугольник окружности к длине радиуса описанной окружности будет наибольшим?
РЕШЕНИЕ:
По условию отношение длины радиуса вписанной в данный треугольник окружности к длине радиуса описанной окружности будет наибольшим?
РЕШЕНИЕ:
По условию  , ,  , ,  . .
 Обозначим Обозначим  , ,  .
В .
В  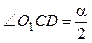 и и  , ,  по теореме синусов для по теореме синусов для  .
Введем функцию .
Введем функцию
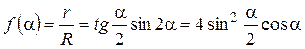 ; ;
   ; ;
 при при  или или  , что не удовлетворяет условию, , что не удовлетворяет условию,  , ,  , ,  , , 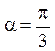 . В точке . В точке  функция функция  имеет максимум имеет максимум
Отношение | ||||||||||||||||
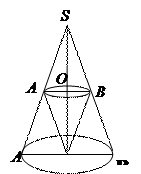
| №22 | Прямой круговой конус с наибольшим объемом вписан в данный конус так, что вершина внутреннего конуса находится в центре основания данного конуса. Докажите, что высота внутреннего конуса составляет одну треть высоты данного конуса.
РЕШЕНИЕ:
Обозначим  , , 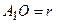 , , 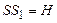 , ,  , ,  . .
 ~ ~  : :  . .
 . .
Вблизи | ||||||||||||||||
| №23 | Шоссе пересекает местность с запада на восток. В 9 км к северу от шоссе находится лагерь, а в 15 км к востоку от ближайшей на шоссе к лагерю точки расположен город. Каков должен быть маршрут, чтобы добраться в город в кратчайший срок, если скорость движения по полю 8 км/час, а по шоссе – 10 км/час?
РЕШЕНИЕ:
Пусть лагерь располагается в точке  , а город в точке , а город в точке  . .  – кратчайший маршрут до шоссе – кратчайший маршрут до шоссе  , ,  км, км,  км. Где будет находиться точка км. Где будет находиться точка  ? ?
 Обозначим расстояние Обозначим расстояние  через через  , ,  . .  , ,  .
Время движения определяется функцией .
Время движения определяется функцией  . Производная . Производная  обращается в ноль при обращается в ноль при  , откуда , откуда 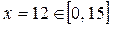 . Значение . Значение 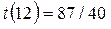 , оно является наименьшим по сравнению с , оно является наименьшим по сравнению с  и и  , так что к шоссе нужно выйти в 12 км от лагеря на восток. , так что к шоссе нужно выйти в 12 км от лагеря на восток.
| ||||||||||||||||
| №24 | Между двумя портами, удаленными друг от друга на расстояние 1200 км, с постоянной скоростью курсирует теплоход. Затраты на рейс в одном направлении слагаются из двух частей. Первая часть, связанная с обслуживанием пассажиров, пропорциональна времени нахождения в пути, другая, обусловленная стоимостью топлива, пропорциональна кубу скорости движения. Найти скорость, с которой должен идти теплоход, чтобы затраты на рейс были минимальны, если известно, что при скорости 90 км/час затраты равны 11,61 тысяч рублей, причем стоимость обслуживания пассажиров составляет  стоимости топлива.
РЕШЕНИЕ:
Пусть стоимости топлива.
РЕШЕНИЕ:
Пусть  – скорость теплохода, тогда время движения в одном направлении – скорость теплохода, тогда время движения в одном направлении  . Затраты на рейс . Затраты на рейс  , ,  , где , где  – коэффициенты пропорциональности. Найдем их из условий – коэффициенты пропорциональности. Найдем их из условий  и и  , ,

 .
Производная .
Производная
 при
при 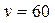 .
Исследуя знак производной, можно показать, что при .
Исследуя знак производной, можно показать, что при 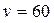 км/час затраты на рейс будут минимальны. км/час затраты на рейс будут минимальны.
| ||||||||||||||||
| №25 | Три бригады должны выполнить работу. Первая бригада делает в день 200 деталей, вторая – на 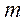 деталей меньше, чем первая деталей меньше, чем первая  , а третья – на , а третья – на  деталей больше, чем первая. Сначала первая и вторая бригады, работая вместе, выполняют деталей больше, чем первая. Сначала первая и вторая бригады, работая вместе, выполняют  всей работы, а затем все три бригады, работая вместе, выполняют оставшиеся всей работы, а затем все три бригады, работая вместе, выполняют оставшиеся  работы. На сколько деталей в день меньше должна делать вторая бригада, чем первая, чтобы вся работа была выполнена указанным способом как можно скорее?
По условию вторая бригада делает в день работы. На сколько деталей в день меньше должна делать вторая бригада, чем первая, чтобы вся работа была выполнена указанным способом как можно скорее?
По условию вторая бригада делает в день  , а третья , а третья  деталей. Обозначим общее число деталей через деталей. Обозначим общее число деталей через  . Время всей работы . Время всей работы
 .
Производная .
Производная  при
при  .
Исследуя знак производной, можно убедиться, что при .
Исследуя знак производной, можно убедиться, что при  функция функция  достигает минимума, и работа будет сделана за наименьшее время, если вторая бригада будет делать на 125 деталей в день меньше, чем первая. достигает минимума, и работа будет сделана за наименьшее время, если вторая бригада будет делать на 125 деталей в день меньше, чем первая.
| ||||||||||||||||
Задачи для самостоятельного решения.
| № п/п | ЗАДАЧИ | ||||||||||||||||||||||||||||||||||||||||
| №1 | Найдите интервалы монотонности и точки экстремума функции  .
ОТВЕТ:
Функция .
ОТВЕТ:
Функция  возрастает при возрастает при  ; убывает при ; убывает при  ; ;  – точка минимума. – точка минимума.
| ||||||||||||||||||||||||||||||||||||||||
| №2 | Найдите экстремумы функции  .
ОТВЕТ: .
ОТВЕТ:
Вид графика функции
| ||||||||||||||||||||||||||||||||||||||||
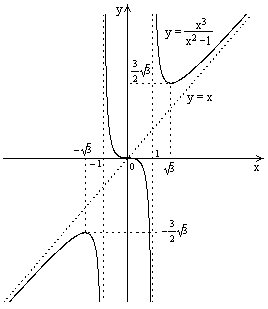
| №3 | Постройте график функции 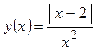 . .
 ОТВЕТ: ОТВЕТ:
| ||||||||||||||||||||||||||||||||||||||||
| №4 | Исследуйте функцию  на возрастание (убывание) и экстремумы.
ОТВЕТ:
при на возрастание (убывание) и экстремумы.
ОТВЕТ:
при  функция убывает;
при функция убывает;
при  функция возрастает,
в точках функция возрастает,
в точках  достигается максимальное достигается максимальное 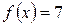 ,
а в точках ,
а в точках  – минимальное – минимальное  значения функции значения функции  . .
| ||||||||||||||||||||||||||||||||||||||||
| №5 | Исследуйте функцию  и постройте её график.
ОТВЕТ: и постройте её график.
ОТВЕТ:
 Функция является убывающей и не имеет экстремумов. Функция является убывающей и не имеет экстремумов.
| ||||||||||||||||||||||||||||||||||||||||
| №6 | Исследуйте функцию  и постройте её график.
ОТВЕТ: и постройте её график.
ОТВЕТ:
График | ||||||||||||||||||||||||||||||||||||||||
| №7 | Исследуйте функцию  и постройте её график.
ОТВЕТ: и постройте её график.
ОТВЕТ:
График
| ||||||||||||||||||||||||||||||||||||||||
| №8 | Найдите наибольшее и наименьшее значения функции  на на  .
ОТВЕТ: .
ОТВЕТ:
 , ,  для для  . .
| ||||||||||||||||||||||||||||||||||||||||
| №9 | По двум взаимно перпендикулярным дорогам по направлению к перекрестку движутся две автомашины со скоростями  и и  . Определите минимальное в процессе движения расстояние между машинами, если в начальный момент времени расстояния машин от перекрестка были равны . Определите минимальное в процессе движения расстояние между машинами, если в начальный момент времени расстояния машин от перекрестка были равны  и и  соответственно.
ОТВЕТ: соответственно.
ОТВЕТ:

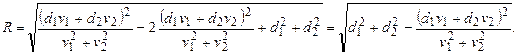
| ||||||||||||||||||||||||||||||||||||||||
Дата добавления: 2020-04-08; просмотров: 257; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!











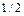

 будет наибольшим и равным
будет наибольшим и равным  при
при  .
.
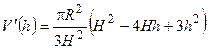 ,
,  при
при  , откуда
, откуда  , что не удовлетворяет условию и
, что не удовлетворяет условию и  .
.
 меняет знак с + на –, значит, при
меняет знак с + на –, значит, при 







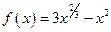 .
.




























 имеет вид
имеет вид 





 имеет вид:
имеет вид: