Рекомендовано Методическим советом ФГАОУ ВПО УРФУ
Кинематика СТО
Задача 1.1. Две релятивистских частицы движутся под прямым углом друг к другу в лабораторной системе отсчета со скоростями v 1 и v 2. Найти их относительную скорость [1].
Решение. Относительной называется скорость, с которой одна частица движется относительно другой. Пусть первая частица движется в системе отсчета К вдоль оси х: v 1 x =[U5] v 1 , v 1 y =0. Тогда для второй частицы v2x =0, v 2 y = v 2. Свяжем с первой частицей систему К´ (ее скорость относительно системы К V = v1). В этой системе отсчета первая частица покоится, следовательно, скорость второй частицы в системе К´ и будет равна относительной скорости. Применяя соотношения для преобразования скоростей, получим
 ,
,  ,
,
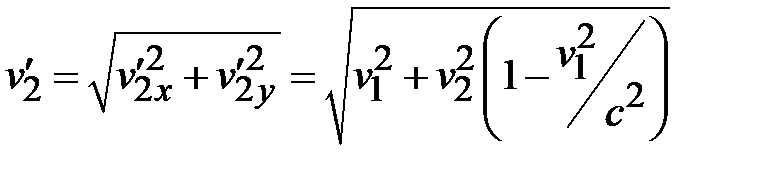 .
.
Рассмотрим в качестве конкретного примера случай, когда v 1 = v 2 = c : v ´2= c . В этой задаче можно задать еще один вопрос: какова скорость сближения этих частиц? И ответ будет таков: 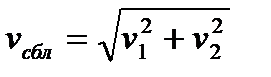 . И если v 1 = v 2 = c, то
. И если v 1 = v 2 = c, то  и в этом нет никакого противоречия с положениями теории относительности. Ведь там говорится о том, что скорость света – это предельная скорость движения материальных объектов, а скорость сближения - это просто скорость сближения.
и в этом нет никакого противоречия с положениями теории относительности. Ведь там говорится о том, что скорость света – это предельная скорость движения материальных объектов, а скорость сближения - это просто скорость сближения.
[U6]
[U7]
Задача 1.2. Два стержня одинаковой собственной длины l 0 движутся в продольном направлении навстречу друг другу параллельно общей оси с одной и той же скоростью v относительно лабораторной системы отсчета. Чему равна длина одного стержня в системе отсчета, связанной с другим ??[1].
|
|
|
Решение. Прежде всеговсего, вспомним, что собственной называется длина l 0 стержня в системе отсчета, относительно которой стержень покоится. Его длина l в системе отсчета, относительно которой он движется, будет меньше, и будет определяться формулой
 .
.
Для того, чтобы найти длину одного стержня в системе отсчета, связанной с другим, необходимо знать скорость этого стержня относительно второго. По сутисути, задача свелась к предыдущей. Свяжем систему К´ со стержнем, движущимся вдоль оси х. Ее скорость V = v. Скорость второго стержня в лабораторной системе отчета v 2 x = -[U8] v , поэтому его скорость v 2 ´ в системе К´ будет равна
 .
.
Подставим это выражение в формулу (1.22) и получим ответ:
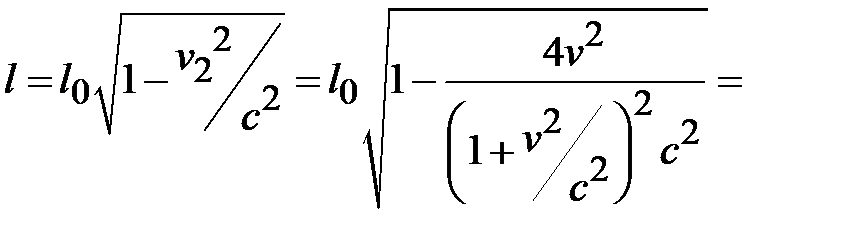
 .
.
Задача 1.3. Две нестабильных частицы движутся в К-системе отсчета по некоторой прямой в одном направлении со скоростью v = 0,990 с. Расстояние между ними в этой системе отсчета l = 120 м. В некоторый момент обе частицы распались одновременно в системе отсчета, связанной с ними. Какой промежуток времени между моментами распада обеих частиц наблюдали в К -– системе? Какая частица распалась позже в К - системе? [1].
|
|
|
Решение. Уже из формулировки вопросов этой задачи следует, что понятие одновременности событий в релятивистской механике не является абсолютным – события, одновременные в одной системе отсчета, оказываются неодновременными в другой. Этот эффект носит название относительности одновременности событий.
Найдем промежуток времени между моментами распада обеих частиц в К-системе, используя обратные преобразования Лоренца :
 .
.
Учитывая, что
V = v ,  и
и  ,
,
Получаем ответ
 .
.
Так как Δ[U9] t >0 , то вторая частицараспалась позже в К-системе.
Задача 1.4. CтерженьСтержень движется равномерно в продольном направлении мимо двух меток А и В, расположенных на расстоянии D х друг от друга. Сначала в момент t 1 [U10] напротив метки А оказался передний конец стержня. Затем напротив метки В в моменты t 2 и t 3 оказались соответственно передний и задний концы стержня. Найти его собственную длину [1].
Решение. Скорость стержня относительно лабораторной системы отсчета легко найти, если учесть что за время  передний конец стержня переместился от метки А до метки В, то есть на расстояние D x:
передний конец стержня переместился от метки А до метки В, то есть на расстояние D x:
|
|
|

Длину стержня l влабораторной системе отсчета определим исходя из того, что передний и задний концы стержня прошли метку В в моменты времени  и
и 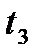 :
:

Для того, чтобы найти собственную длину стержня  , то есть его длину в системе отсчета, относительно которой стержень покоится, воспользуемся формулой
, то есть его длину в системе отсчета, относительно которой стержень покоится, воспользуемся формулой

тогда

Задача 1.5. На диаграмме пространства-времени (см. рис. 1.51) показаны три события А, В и С, которые произошли на оси x некоторой инерциальной системы отсчета. Найти :
а) промежуток [U11] времени между событиями А и В в той системе отсчета, где оба события произошли в одной точке ;
б) расстояние между точками, где произошли события А и С, в той системе отсчета, где они одновременны [1].[U12]

Рис. 1.1[U13]
Решение. Пусть диаграмма, изображенная на рисунке, соответствует инерциальной системе отсчета К .[U14] Найдем интервал, разделяющий события А и В в этой системе отсчета :
 .
.
| ct , м |
| х, м |
| А |
| B |
| C |
| 3 |
| 3 |
| 6 |
| 6 |
| 0 |
 , а поскольку
, а поскольку 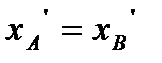 , то
, то 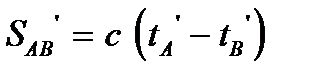 .
. |
|
|
Как отмечалось выше, интервал, разделяющий два события, одинаков в различных системах отсчета. Поэтому  и, следовательно,
и, следовательно,
 .
.
Подстановка числовых значений дает результат 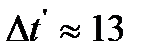 нс.
нс.
Рассмотрим теперь систему отсчета К’’, в которой события А и С произошли одновременно. Интервал, разделяющий эти события в системе К’’, равен
 .
.
Вследствие инвариантности интервала  .Возведем в квадрат обе части этого равенства и, учитывая одновременность событий А и С в системе К’’, получим
.Возведем в квадрат обе части этого равенства и, учитывая одновременность событий А и С в системе К’’, получим

Таким образом расстояние между событиями А и С в системе К’’ будет равно
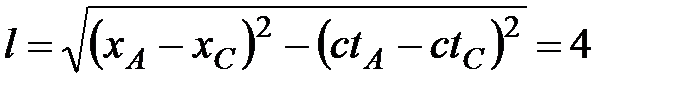 м.
м.
Задача 1.6. В К-системе отсчета мю-мезон, движущийся со скоростью v = 0,990 с , пролетел от места своего рождения до точки распада расстояние l = 3,0 км. Определить :
а) собственное время жизни этого мезона ;
б) расстояние, которое пролетел мезон в К-системе с «его собственной точки зрения» [1].
Решение. Найдем время жизни мезона в лабораторной системе отсчета К
 Используя соотношение (1.30), связывающее собственное время жизни движущегося мезона с его временем жизни в системе К , получим
Используя соотношение (1.30), связывающее собственное время жизни движущегося мезона с его временем жизни в системе К , получим
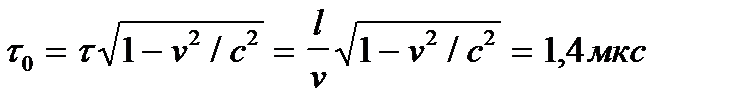 .
.
Расстояние, которое пролетел мезон в К - системе с «его собственной точки зрения», определяется формулой
 км.
км.
Задача 1.7. Стартовавшая с Земли воображаемая космическая ракета движется с ускорением aˊ = 10 g , одинаковым в каждой инерциальной системе, мгновенно сопутствующей ракете. Разгон продолжался по земному времени  год. Найти, на сколько процентов отличается скорость ракеты от скорости света в конце разгона. Каков путь, пройденный ракетой к этому моменту ? [1].
год. Найти, на сколько процентов отличается скорость ракеты от скорости света в конце разгона. Каков путь, пройденный ракетой к этому моменту ? [1].
Решение. Воспользуемся формулой (1.20), связывающей между собой ускорения в системах К и К’ ,, в которой учтем, что

 :
:

Преобразуем это выражение к виду[U15]

и проинтегрируем его
 .
.
Интегрирование правой части является элементарным и дает 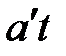 . . Интеграл в левой части этого выражения является табличным:
. . Интеграл в левой части этого выражения является табличным:

Проводя соответствующие подстановкиподстановки, приходим к равенству

откуда получаем зависимость скорости ракеты от времени
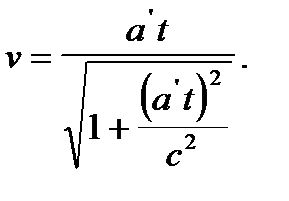
Проанализируем полученное выражение. При 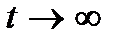
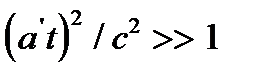 и, следовательно,
и, следовательно,  поэтому
поэтому 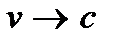 .
.
При 

Для ответа на вопрос о том, на сколько процентов скорость ракеты в конце разгона отличается от скорости света, необходимо найти отношение

 .
.
Найдем путь l, пройденный ракетой за время разгона. Для этого воспользуемся соотношением
| = |
| 0 |

 светового года.
светового года.
Напомним, что световой год - [U16] это расстояние, которое свет проходит за один год. Он равен 
Динамика СТО
Задача 2.1. Какую работу надо совершить, чтобы увеличить скорость частицы с массой m от 0,60с до 0,80с? Сравнить полученный результат со значением, вычисленным по нерелятивистской формуле [1].
Решение. По теореме о кинетической энергии изменение кинетической энергии частицы равно работе сил, действующих на нее, поэтому
 .
.
В релятивистском случае кинетическая энергия определяется формулой

В случае нерелятивистском

Задача 2.2. Пучок релятивистских частиц с кинетической энергией Wk падает на поглощающую мишень. Сила тока в пучке равна I, заряд и масса – е и m . Найти силу давления пучка частиц на мишень и выделяющуюся в ней мощность Р [1].
Решение. На первый вопрос этой задачи мы ответим очень просто, если применим второй закон Ньютона и зависимость импульса частицы от её кинетической энергии формулу (2.26):
 .
.
Поясним, что Δ N – это число частиц, падающих на мишень за время Δ t , Δ N е – заряд, попадающий на мишень за это время, значит Δ N е/ Δ t – сила тока в пучке.
Когда говорят про мощность, то обычно вспоминают работу, время и так далее. Здесь идет речь о другом. В мишени выделяется энергия, и мощность в данном случае – это энергия, выделяемая в ней в единицу времени. Поэтому
 .
.
Задача 2.3. Частица массы m движется вдоль оси х по закону  , где d – постоянная, с – скорость света, t – время. Найти силу, действующую на частицу [1].
, где d – постоянная, с – скорость света, t – время. Найти силу, действующую на частицу [1].
Решение. Для начала найдем скорость частицы
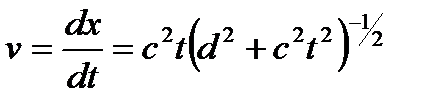
и ее импульс
 .
.
Нам осталось найти силу:
 .
.
Сила – постоянная. Любопытно, кстати, - скорость стремится к определенному пределу (к скорости с) и практически устанавливается, а импульс продолжает расти по линейному закону.
Задача 2.4. Нейтрон с кинетической энергией Wk =2mc2, где m - его масса, налетает на другой, покоящийся нейтрон. Найти в системе их центра масс:
а) суммарную кинетическую энергию Wk´ нейтронов;
б) импульс р´ каждого нейтрона [1].
Решение. воспользуемся Воспользуемся инвариантом который запишем в виде
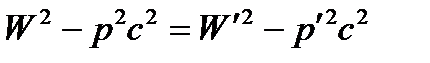 ,
,
где слева стоят энергия и импульс двух нейтронов в лабораторной системе отсчета, а справа – энергия и импульс этих нейтронов в системе отсчета, связанной с их центром масс.
Запишем их в явном виде.
 .
.
В этом выражении мы учли, что в лабораторной системе отсчета один из нейтронов покоится, а второй движется и обладает кинетической энергией Wk. Импульс этого нейтрона (и, значит, всей системы) равен
 .
.
В системе центра масс нейтронов их суммарный импульс равен нулю: р´=0, а энергию можно записать в виде
 .
.
Подставим полученные выражения для энергии и импульсы в инвариант и получим ответ на первый вопрос задачи:
 ,
,
 .
.
Для того, чтобы ответить на второй вопрос, учтем, что в системе центра масс импульсы нейтронов равны по величине, следовательно равны и их кинетические энергии. А это значит, что мы можем найти кинетическую энергию одного нейтрона

и найти его импульс:
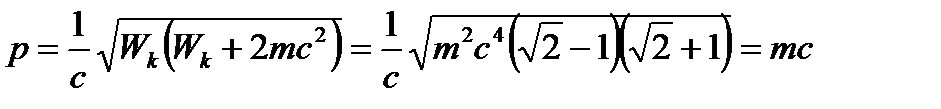 .
.
Задача 2.5. Так как период обращения электронов в однородном магнитном поле с ростом энергии резко увеличивается, циклотрон оказывается непригодным для их ускорения. Этот недостаток устраняется в микротроне (см. рис. 2.1), где изменение периода обращения электрона ΔТ делают кратным периоду ускоряющего поля Т0. Сколько раз электрону необходимо пройти через ускоряющий промежуток микротрона, чтобы приобрести энергию W = 4,6 МэВ, если ΔТ = Т0 , индукция магнитного поля В = 107 мТл и частота ускоряющего поля ν = 3000 МГц? [1].

Рис. 2.1
 Решение. Рассмотрим изменение периода обращения электрона, которое возникло при прохождении им n -гои n -1-гооборотов. Для этого вспомним формулу, которая описывает зависимость периода обращения заряда в поперечном магнитном поле:
Решение. Рассмотрим изменение периода обращения электрона, которое возникло при прохождении им n -гои n -1-гооборотов. Для этого вспомним формулу, которая описывает зависимость периода обращения заряда в поперечном магнитном поле:

где m – масса заряда q, В – индукция магнитного поля. С учетом релятивистского изменения массы получим

Тогда
 ,
,
где un и un -1 – скорости электрона при прохождении им n-гои n -1-го оборотов.
А теперь обратимся к формуле
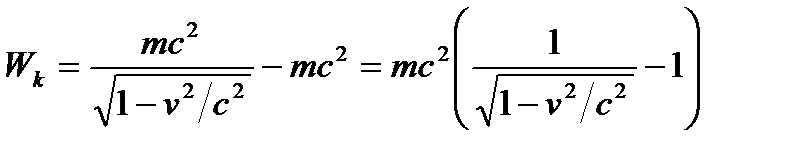 . (
. (
и преобразуем ее к виду
 .
.
Подставим это выражение в формулу для изменение периода обращения электрона ΔТ и получим
 ,
,
или
 ,
,
где Wn и Wn-1 – кинетические энергии электрона при прохождении им n -го и n -1-гооборотов, ΔW = Wn – Wn -1 . Далее учтем, что ΔТ=Т0 =1/ν , и найдем число оборотов N по понятной формуле:
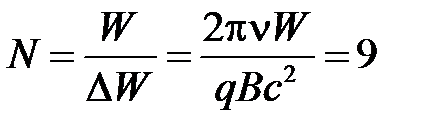 .
.
Задача 2.6. Чтобы в циклотроне не возникала расстройка, вызванная изменением периода обращения частицы при возрастании ее энергии, медленно изменяют (модулируют) частоту ускоряющего поля. По какому закону надо изменять эту частоту  , если индукция магнитного поля постоянна и равна В и частица приобретает за один оборот энергию
, если индукция магнитного поля постоянна и равна В и частица приобретает за один оборот энергию  . Заряд частицы q, масса m [1].
. Заряд частицы q, масса m [1].
Решение. Итак, мы хотим разогнать частицу до релятивистских скоростей. При этом ее период обращения начинает зависеть от скорости частицы по закону
 .
.
Кинетическая энергия релятивистской частицы определяется формулой
 .
.
Посчитаем скорость изменения кинетической энергии, то есть возьмем ее производную по времени
 .
.
С другой стороны, скорость изменения кинетической энергии частицы можно определить как отношение
 .
.
Приравняем правые части этих выражений
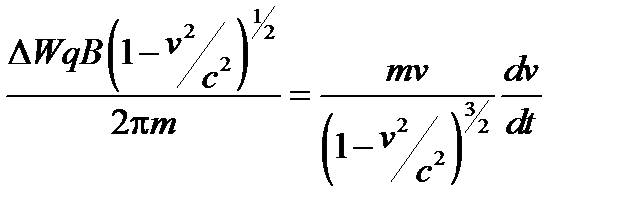 ,
,
преобразуем их и проинтегрируем полученное равенство:
 ,
,  .
.
Отсюда

и мы получаем окончательное выражение
 ,
,
которое можно записать в более компактной форме, если ввести обозначения
 ,
, 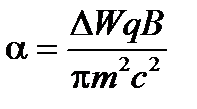 ,
,  .
.
В заключение отметим, что частицы в фазотроне ускоряются до энергий порядка 1 ГэВ (на два порядка больше, чем в циклотроне!) и ограничения определяются в основном размерами фазотрона, так как с увеличением скорости частиц растет радиус их орбиты.
Циклотрон применяют для ускорения тяжелых заряженных частиц – протонов и ионов. Использовать циклотрон для ускорения легких частиц (например, электронов) не эффективно – у них малая масса, они быстро разгоняются до больших скоростей, возникают релятивистские эффекты и появляется расстройка, о которой мы уже говорили выше. Для их ускорения применяют другие устройства – одно из них, микротрон, мы рассмотрели в предыдущей задаче.
Задача 2.7. Два протона движутся навстречу друг другу с одинаковыми кинетическими энергиями Wk (в К-системе отсчета). Найти кинетическую энергию Wk ˊ одного протона относительно другого [1].
Решение. Воспользуемся инвариантностью величины W 2 – p 2 c 2, записав ее в К-системе (она является одновременно и системой центра масс), и в системе отсчета Кˊ, связанной с одним из протонов:

Рассмотрим члены, входящие в это равенство. В системе К энергия протонов определяется суммой их кинетических энергий (они равны) и энергий покоя:
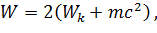
а их суммарный импульс равен нулю (К-система является системой центра масс). В системе Кˊ один протон покоится, а второй движется, обладая кинетической энергией W ˊ k , поэтому W ˊ = W ˊ k +2mc 2. Суммарный импульс этих протонов в системе Кˊ равен импульсу одного протона (второй - покоится)

Исходное равенство принимает вид

откуда

Полученный результат заслуживает того, чтобы обсудить его более подробно. Пусть кинетическая энергия протонов в К-системе Wk = 50 ГэВ, mc 2 для протона порядка 1 ГэВ. Тогда W ˊ k = 5·103 ГэВ! Возможность получения такого большого «выигрыша» в энергии лежит в основе метода встречных пучков на современных ускорителях.
Задача 2.10. Пороговая энергия (минимальная энергия, необходимая для осуществления данного процесса). Найти пороговую энергию  фотона для рождения пары электрон-позитрон в поле покоящегося ядра массы M [1].
фотона для рождения пары электрон-позитрон в поле покоящегося ядра массы M [1].
Решение. Вновь воспользуемся инвариантностью величины W 2 – p 2 c 2 (формула (2.25)) и запишем ее до взаимодействия в К-системе (в ней ядро покоится), а после взаимодействия – в системе отсчета Кˊ, которая является системой центра масс ядра и пары электрон-позитрон:

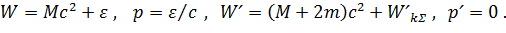
В дополнение к данным в условии обозначениям отметим, что m – это масса электрона (позитрон имеет такую же массу), импульс фотона р мы определили из формулы (2.22), а рˊ - это суммарный импульс ядра и родившейся пары электрон-позитрон. Он равен нулю, так как Кˊ - это система центра масс.  – суммарная кинетическая энергия частиц в Кˊ - системе. Учтем, что на пороге реакции (
– суммарная кинетическая энергия частиц в Кˊ - системе. Учтем, что на пороге реакции (  ) она равна нулю.
) она равна нулю.
Тогда

и после несложных преобразований мы получает ответ

Видно, что для рождения пары энергия фотона должна быть больше, чем 2mc2.
В основе этой задачи лежит очень важное явление, связанное с распространением в веществе жесткого электромагнитного излучения, которое сопровождается рождением электрон-позитронных пар в поле атомных ядер. Для их рождения необходимо, чтобы энергия фотона была больше, чем 2mc2=1,02 МэВ (при этом наименьшая частота фотона должна быть порядка 2,5·1020 Гц, а длина волны – меньше, чем 1,2·10-12 м). подчеркнемПодчеркнем, что если фотоэффект и эффект Комптона происходят в результате столкновения фотона с электронами, то рождение пар происходит при столкновении фотона с ядром.
Чтобы выяснить, какую роль в этом процессе играет ядро, рассмотрим возможность рождения пары в вакууме. Пусть импульс фотона  , импульс электрона
, импульс электрона  и импульс позитрона
и импульс позитрона  .
.
По закону сохранения импульса  , следовательно р
, следовательно р  р1 +р2 . С другой стороны, по закону сохранения энергии ε = W1 + W 2 .
р1 +р2 . С другой стороны, по закону сохранения энергии ε = W1 + W 2 .

из которого следует, что р ˃ р1 +р2 .
Эти взаимно исключающие друг друга неравенства указывают на то, что рождение электрон-позитронной пары в вакууме противоречит законам сохранения энергии и импульса. Этого противоречия не возникает, если вблизи фотона оказывается массивное ядро. При столкновении с фотоном ядро забирает у него избыток импульса, но при этом практически не влияет на энергетический баланс. В этих условиях рождение пары не противоречит законам сохранения. Электрон-позитронная пара может возникнуть и из двух фотонов без участия ядер, но регистрация этого процесса сильно затруднена.
Индивидуальное домашнее задание по теме «Специальная теория относительности»
Задача 1. Найти собственную длину стержня, если в лабораторной системе отсчета его скорость v, длина l =1,00м и угол между ним и направлением движения φ.
Задача 2. С какой скоростью (м/с) двигались в К-системе отсчета часы, если за время t (в К-системе) они отстали от часов этой системы на Δ t.
Задача 3. Два стержня одинаковой собственной длины l=0,5 м движутся в продольном направлении навстречу друг другу с одной и той же скоростью v относительно лабораторной системы отсчета. Чему равна длина каждого стержня в системе отсчета, связанной с другим стержнем?
Задача 4. Какую работу (в МэВ) надо совершить, чтобы увеличить скорость протона от v 1 до v 2?
Задача 5. Вычислить импульс частицы (в МэВ/с), если ее кинетическая энергия равна Wk .
Задача 6. Нейтрон с кинетической энергией Wk налетает на другой, покоящийся нейтрон. Найти в системе их центра масс импульс рˊ каждого нейтрона (в МэВ/с).
Оформление: бумага А4, компьютерный набор - шрифт Times New Roman (14), титульный лист. В конце – сводная таблица ответов. Формулы – в любом редакторе формул.
Внимание! В таблице для каждого варианта приводится свой набор данных.
Все расчеты и ответ должны содержать не менее трех значащих цифр.
Таблица
| Вариант | 1 | 2 | 3 | 4 | 5 | |
| Задание. 1 | v φ[U17] (в 0) | 0,4с 30 | 0,5с 30 | 0,6с 30 | 0,7с 30 | 0,8с 30 |
| Зад. [U18] 2 | t , с Δt , с | 5 0,2 | 10 0,2 | 15 0,2 | 20 0,2 | 25 0,2 |
| Зад. 3 | v | 0.99c | 0.95c | 0.90c | 0.85c | 0.80c |
| Зад. 4 | v1 v2 | 0.30c 0.80c | 0.35c 0.80c | 0.40c 0.80c | 0.45c 0,80с | 0.50c 0,80с |
| Зад.5 | Частица Wk МэВ | п 500 | п 600 | п 700 | п 800 | п 900 |
| Зад. 6 | Wk МэВ | 2000 | 1800 | 1600 | 1400 | 1200 |
| Вариант | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Зад. 1 | 0,5с 45 | 0,6с 45 | 0,7с 45 | 0,8с 45 | 0,9с 45 | 0,85с 45 | 0,99с 45 | 0,4с 60 | 0,5с 60 | 0,6с 60 | 0,7с 60 |
| Зад. 2 | 10 0,4 | 15 0,4 | 20 0,4 | 25 0,4 | 30 0,4 | 35 0,4 | 40 0,4 | 5 0,6 | 10 0,6 | 15 0,6 | 20 0,6 |
| Зад. 3 | 0,55с | 0,50с | 0,45с | 0,40с | 0,35с | 0,30с | 0,25с | 0,20с | 0,25с | 0,975с | 0,925с |
| Зад. 4 | 0,35с 0,90с | 0,40с 0,90с | 0,45с 0,90с | 0,50с 0,90с | 0,55с 0,90с | 0,60с 0,90с | 0,65с 0,90с | 0,30с 0,95с | 0,35с 0,95с | 0,40с 0,95с | 0,45с 0,95с |
| Зад.5 | р 1400 | р 1500 | р 1600 | р 1700 | р 1800 | р 1900 | р 2000 | е 5 | е 10 | е 15 | е 20 |
| Зад. 6 | 2400 | 2600 | 2800 | 3000 | 3200 | 3400 | 3600 | 3800 | 4000 | 4200 | 4400 |
Библиографический список[U19]
1. Иродов И.Е. Задачи по общей физике / И.Е. Иродов. М.: Бином. Лаборатория знаний, 2012.432 с.
http://bib.convdocs.org/v14640/?download=1#5
Учебное электронное текстовое издание
Повзнер Александр Александрович
Малышев Леонид Григорьевич
Шумихина Кямаля Арифовна
СБОРНИК ИНДИВИДУАЛЬНЫХ
ДОМАШНИХ ЗАДАНИЙ ПО ФИЗИКЕ
Ответственный редактор Н.В. Лутова
Редактор А.В. ЕрофееваОвчинникова
Компьютерная верстка авторская
Рекомендовано Методическим советом ФГАОУ ВПО УРФУ
Разрешено к публикации
Электронный формат – pdf
Объем 1,000,50,51,2 уч.-изд. л.

Екатеринбург, ул. Мира, 19
Информационный портал УрФУ
[U1]Рекомендуется оформить титульный лист по образцу из Методических инструкций (титул для текстового документа, а не для презентации)
[U2]Аннотацию рекомендуется перенести на титульный лист (см. образец в МИ)
[U3]рекомендуется оформить, как заголовок первого уровня, только не выставлять уровень, чтобы это слово не попало в оглавление
[U4] [U4]Рекомендуется вставить номера страниц (внизу, по центру, без отступов, использовать шрифт Times New Roman, 12 пт)
[U5]знак равенства рекомендуется отделять пробелами с обеих сторон
[U6]рекомендуется удалять лишние абзацные отступы, не использовать их для форматирования текста
[U7]Рекомендуется удалять лишние абзацные отступы, не использовать их для форматирования текста
[U8]не рекомендуется использовать дефис в качестве знака "минус"
[U9]греческие символы рекомендуется оформлять прямым шрифтом
[U10]рекомендуется удалять лишние пробелы
[U11]рекомендуется использовать возможности текстового редактора для создания списков
[U12]Рекомендуется использовать возможности текстового редактора для создания списков
[U13]рекомендуется добавить к рисункам подписи
[U14]Рекомендуется удалять пробелы перед точками
[U15]Рекомендуется исправлять «висячие» строки
[U16]рекомендуется различать дефис и тире, не использовать одно в значении другого
[U17]греческие символы рекомендуется набирать прямым шрифтом
[U18]рекомендуется не сокращать
[U19]рекомендуется оформить по ГОСТ
Дата добавления: 2020-04-25; просмотров: 4143; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
