Задания для самостоятельной работы.
Дифференцирование сложных функций
Пусть функция  дифференцируема в точке
дифференцируема в точке  и
и 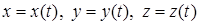 – дифференцируемые функции в точке
– дифференцируемые функции в точке  . Тогда сложная функция
. Тогда сложная функция  также дифференцируема в точке
также дифференцируема в точке  и её производная определяется по правилу
и её производная определяется по правилу
 (1)
(1)
Пример 1. Найти  , если
, если  .
.
Решение. В соответствии с формулой (1) запишем
 .
.
Подсчитаем  и
и  .
.
Значит, 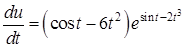 .
.
Можно было сразу записать сложную функцию, зависящую от одной переменной 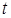

и дифференцировать её. ☻.
Пусть функция  дифференцируема в точке
дифференцируема в точке  и функции
и функции  ,
,  ,
,  дифференцируемы в точке
дифференцируемы в точке  . Тогда сложная функция двух переменных
. Тогда сложная функция двух переменных  тоже дифференцируема в точке
тоже дифференцируема в точке  и её частные производные определяются по правилам
и её частные производные определяются по правилам
 (2)
(2)
Пример 2. Найти  и
и  , если
, если  ,
,  .
.
Решение. Задана сложная функция 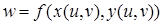 . В соответствии с формулами (2) запишем
. В соответствии с формулами (2) запишем


Подсчитаем производные

Значит,


Можно было сразу записать сложную функцию, зависящую от двух переменных  и дифференцировать её. ☻
и дифференцировать её. ☻
Пример 3. Найти  и
и  функции
функции  .
.
Решение. Введём обозначения промежуточных переменных
 .
.
Подсчитаем частные производные функции  по формулам (2):
по формулам (2):
 ,
,
 .
.
Переходим к вычислению вторых производных. Заметим, что функции  и
и  дифференцируются по тем же правилам, что и заданная функция
дифференцируются по тем же правилам, что и заданная функция  , то есть их частные производные находятся по формулам (2):
, то есть их частные производные находятся по формулам (2):
 ,
,
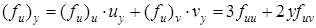 .
.
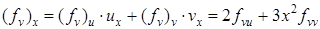 .
.
 .
.
Дифференцируем функции  :
:


 .
.
Здесь принято, что  – дважды дифференцируемая функция и
– дважды дифференцируемая функция и 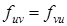 . ☻
. ☻
|
|
|
Пример 4. Найти  и
и  функции
функции  .
.
Решение. Можно, как в предыдущем примере, ввести обозначения промежуточных переменных. Но мы просто пронумеруем переменные:  – первая,
– первая, 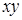 – вторая, тогда
– вторая, тогда  и
и  – частные производные функции
– частные производные функции  по первой и второй промежуточным переменным соответственно. В этих обозначениях по формулам (2):
по первой и второй промежуточным переменным соответственно. В этих обозначениях по формулам (2):
 ,
,
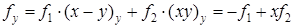 .
.
Продолжаем дифференцирование:



Здесь принято, что  – дважды дифференцируемая функция и
– дважды дифференцируемая функция и 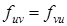 . ☻
. ☻
Задачи для самостоятельной работы
1. Найти производные первого и второго порядков от следующих сложных функций:
1.  ; 2.
; 2.  ;
;
3.  ; 4.
; 4.  .
.
6.  , где
, где  ; 7.
; 7.  , где
, где  ;
;
8.  , где
, где  ; 9.
; 9.  ;
;
10.  ; 11.
; 11.  .
.
2. Найти  , если
, если  .
.
Производная по направлению. Градиент.
Пусть функция  дифференцируема в области
дифференцируема в области  и пусть в этой области задано некоторое направление
и пусть в этой области задано некоторое направление  . Производная функции
. Производная функции  по направлению
по направлению  вычисляется по формуле
вычисляется по формуле
 (1)
(1)
Скорость наибольшего роста функции в данной точке (по величине и направлению) определяется вектором, который обозначается символом  и называется градиентом функции:
и называется градиентом функции:
|
|
|
 (2)
(2)
Пример 1. Найти производную функции  в точке
в точке  в направлении
в направлении  . Чему равна величина градиента функции в этой точке?
. Чему равна величина градиента функции в этой точке?
Решение. Чтобы воспользоваться формулой (1), подсчитаем частные производные в точке  :
:

Значит, производная функции  в заданном направлении равна
в заданном направлении равна
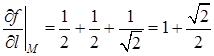 .
.
В соответствии с формулой (2) запишем градиент функции в точке  – вектор
– вектор
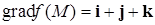
Величина градиента (модуль вектора) равна  . ☻
. ☻
Пример 2. Найти производную функции 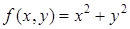 в точке
в точке  в направлении, составляющем угол
в направлении, составляющем угол  с положительным направлением оси
с положительным направлением оси  .
.
Решение. Подсчитаем сначала частные производные в точке  :
:
 .
.
Найдем направляющие косинусы:
 .
.
По формуле (1) запишем
 . ☻
. ☻
Пример 3. Для функции  определить угол между градиентами в точках
определить угол между градиентами в точках  и
и  .
.
Решение. Подсчитаем сначала частные производные:

Теперь можем записать градиент функции в точках  и
и  :
:
 ,
,
 .
.
Очевидно, эти векторы ортогональны – их скалярное произведение равно нулю:  . Значит, угол между градиентами равен
. Значит, угол между градиентами равен  . ☻
. ☻
Задания для самостоятельной работы.
|
|
|
1. Найти производную функции  в точке
в точке  в направлении, идущем от этой точки к точке
в направлении, идущем от этой точки к точке  .
.
2. Найти производную функции  в точке
в точке  в направлении биссектрисы первого координатного угла.
в направлении биссектрисы первого координатного угла.
3. Найти производную функции  в точке
в точке  в направлении, идущем от этой точки к началу координат.
в направлении, идущем от этой точки к началу координат.
4.  . Найти
. Найти  в точке
в точке  .
.
5.  . Найти
. Найти  в точке
в точке  .
.
6.  . Найти
. Найти  в точке
в точке  .
.
7.  . Найти угол между градиентами этой функции в точках
. Найти угол между градиентами этой функции в точках  и
и  .
.
8. Даны функции  и
и  . Найти угол между градиентами этих функций в точке
. Найти угол между градиентами этих функций в точке  .
.
9. Найти точку, в которой градиент функции  равен
равен 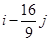 .
.
10. Найти точки, в которых модуль градиента функции  равен 2.
равен 2.
11. Найти наибольшую крутизну подъема поверхности  в точке
в точке  .
.
12. Найти наибольшую крутизну подъема поверхности  в точке
в точке  .
.
Дата добавления: 2020-04-25; просмотров: 83; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
