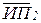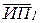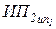Задача №1. Равноточные измерения.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«КЕРЧЕНСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ ТЕХНОЛОГИЧЕСКИЙ
УНИВЕРСИТЕТ»
Кафедра «Судовождение и промышленное рыболовство»
Пазынич Г.И.
Математические основы судовождения
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
По выполнению курсовой работы
Курсантами третьего курса очной и заочной формы обучения
Специальности 26.05.05 «Судовождение»
Керчь, 2015 г.
УДК 656.61.052:51
Составитель: Пазынич Г.И., канд.техн.наук, доцент кафедры «Судовождение и промышленное рыболовство» ФГБОУ ВО «КГМТУ»
______________
Рецензент: Куценко Д.Г., ШДП, ассистент кафедры «Судовождение и
промышленное рыболовство» ФГБОУ ВО «КГМТУ» ___________
Методические указания рассмотрены и одобрены на заседании кафедры “Судовождение и промышленное рыболовство” ФГБОУ ВО «КГМТУ»,
протокол № 2 от 22.10. 2015 г.
Зав. кафедрой ___________ Г.И. Пазынич
Методические указания утверждены и рекомендованы к публикации на заседании методической комиссии МФ ФГБОУ ВО «КГМТУ»,
протокол № ___ от _________ 2015 г.
ФГБОУ ВО «КГМТУ», 2015 г.
Содержание
Введение 5
Раздел 1 Математическая обработка результатов наблюдений 6
|
|
|
1.1 Расчеты количественных характеристик погрешностей навигационных
параметров 6
1.2 Расчеты погрешностей навигационных параметров
изменяющихся во времени и определение доверительных оценок 10
1.3 Обработка статистических данных методами линейной корреляции 14
Раздел 2. Способы определение места судна 18
2.1 Определение места судна (ОМС) методом изолиний 18
2.2 Графоаналитический метод 20
2.3 Влияние случайных ошибок измерений на точность места,
определяемого по двум ЛП 21 2.4 Графические методы отыскание вероятнейшего места судна
при избыточном числе линий положения 23
2.5 Аналитическое определение места судна и оценка точности
|
|
|
Задания для выполнения задач раздела 1 30
Задания для выполнения задач раздела 2 39
Список рекомендованной литературы 53
Введение
Методические указания по выполнению курсовой работы составлены для учебной дисциплины «Математические основы судовождения», котораяпредназначена для уровня основной образовательной программы – специалист. Специальность - 26.05.05 «Судовождение». Профиль – «Промысловое судовождение». Статус дисциплины – базовая. Она включена в учебный план набора, начиная с 2015 года
Методические указания составлены в соответствии с рабочей программой отвечающей требованиям ФГОС ВО, компетенций МК ПДМНВ-78 с поправками и рабочего учебного плана с учетом требований ООП и рекомендаций модельных курсов ИМО 3.08, 7.03.
Выполнение курсовой работы направлено на закрепление знаний:
|
|
|
- фундаментальных понятий судовождения и правил использования Мореходных таблиц;
- правил и методов рациональных расчетов и вычислений с заданной точностью;
- теоретических основ морской картографии и построения картографических проекций;
- причин и видов погрешностей измерений;
- свойств и особенностей различных ошибок измерений навигационных параметров с учетом их влияния на безопасность мореплавания;
Теоретических основ получения и использования навигационных изолиний и линий положения (ЛП);
- влияния точности измерений параметров на точность изолиний или ЛП с характеристиками их точности;
- методов получения вероятнейшего места судна и оценки его точности.
На основании выполнения курсовой работы студенты должны уметь:
Уметь:
- вести расчеты искомых величин различными методами с точностью не ниже точности исходных данных;
- выполнять измерения навигационных параметров и определять точность полученных результатов при равноточных и разновесных измерениях;
- на основе анализа точности измерений определять корреляционную связь между измеренными величинами;
- применять знания по ОМС и оценке его точности при решении всех специальных задач судовождения;
|
|
|
- вычислять значения навигационных параметров и их градиенты;
- выполнять расчеты для определения обсервованных координат места судна с оценкой их точности, в том числе и при использовании избыточной навигационной информации;
Мореходных таблиц и с применением вычислительной техники);
- способностью обосновывать решения на основе выработанных знаний и умений выполнения необходимых навигационных расчетов при использовании официальных справочных изданий – мореходных таблиц, наставления по организации штурманской службы на судах флота рыбной промышленности, устава службы на судах флота рыбной промышленности.
РАЗДЕЛ 1
МАТЕМАТИЧЕСКАЯ ОБРАБОТКА СТАТИСТИЧЕСКИХ ДАННЫХ.
1.1 Расчеты количественных характеристик
погрешностей навигационных параметров
1.1.1 Обработка результатов равноточных измерений навигационных параметров
Все наблюдения навигационных параметров, да и не только их, сопровождаются ошибками. Судоводитель в своей работе обязан уметь обрабатывать различные параметры, содержащие ошибки.
Эти ошибки по своим свойствам и характеру можно разбить на три основные группы:
· систематические ошибки это ошибки, характер и причины, возникновения которых известны или предвидимы. Рациональной методикой измерений и определёнными способами обработки результатов, влияние этих ошибок можно не только ослабить, но и исключить.
· Случайные ошибки это ошибки, которые вызваны многообразными и противоречивыми причинами, не поддающимися учёту и существенно не связанные с производством наблюдений, а их величина и знак для каждого измерения свои.
· Промахи определяются как неверные наблюдения или просчёты выходящие за пределы точности данного ряда измерений. Промахи из дальнейшей обработки исключаются.
Обработка наблюдений содержащих систематические ошибки будет рассмотрена в дальнейших работах.
Экспериментально установлено, что почти всегда случайным ошибкам измерения присущи следующие свойства:
1) среднее значение случайных ошибок близко к нулю;
2) вероятность появления ошибок равных по значению, но противоположных по знаку, одинакова;
3) численно небольшие ошибки более вероятны, чем численно большие;
4) случайные ошибки не могут превзойти некоторых границ, связанных с точностью производимых измерений;
5) внутри этих границ случайные ошибки могут принимать любые значения в соответствии с подпунктами 2 и 3.
Одной из важнейших характеристик случайных величин является вероятнейшее значение измеренной величины и оценка его точности.
Для того, что бы уменьшить влияние случайной ошибки, производится
некоторое количество n измерений навигационного параметра a.
Предположим, что все наблюдения производились одним наблюдателем, в одинаковых условиях, одним прибором, настройка которого не менялась в процессе наблюдений, такие наблюдения принято называть равноточными или равновесными.
В результате таких наблюдений мы получим n близких к истинному a ист значений а1, a 2 ... an, каждое из которых содержит некоторую ошибку. Так как a ист нам не известно, то и точное значение этих ошибок нам так же неизвестно.
Очевидно, что наиболее близким т.е. вероятнейшим значением a вер к истинному значению a ист будет среднее арифметическое ряда равновесных измерений свободных от систематических ошибок:
|
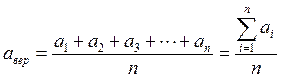
Необходимо понимать, что формула (8) соответствует фактической мере точности измерений h. Поэтому, если, например, измерения выполняют линейкой разбитой на миллиметры, то ни увеличением числа измерений, ни увеличением числа знаков при вычислениях, ни колдовством нельзя получить результат с точностью, скажем, до 0,01 мм.
Мы уже говорили о том, что каждое из измерений содержало ошибку. Критерием точности единичного измерения на практике чаще всего применяют среднюю квадратичную погрешность m, вычисляемую по формуле
|
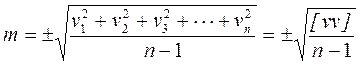
где, vi уклонения отдельных измерений ai от a вер: vi = a вер – ai , соответственно [ vv ] – сумма квадратов отклонений.
В случае, когда истинное значение параметра a ист известно, СКП рассчитывается по формуле:
|
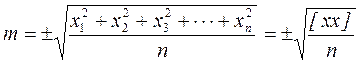
где, xi ошибки отдельных измерений ai: xi = a ист – ai , соответственно [ xx ] – сумма квадратов ошибок.
Критерий точности единичного измерения СКП m даёт нам вероятность случайной ошибки x в границах от – m до m примерно 68.3%.
|
m пред =3 m
называемая предельной ошибкой одного измерения, накрывающая ошибки измерений с вероятностью 99.7%. Измерение у которых уклонения v превышают m пред, объявляются промахами и из обработки исключаются.
Способ определения СКП одного (любого) измерения по формулам (9), (10) называется методом внутренней сходимости.
|
m = knR ,
где R – размах, т.е. разность между максимальным и минимальным значением измеряемой величины
R = amax – amin
kn – коэффициент, который зависит от числа измерений в серии, его значения приводятся в таблице 2.
Таблица 2.
| n | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| kn | 0.430 | 0.395 | 0.370 | 0.351 | 0.337 | 0.325 | 0.315 |
Из всего вышесказанного можно сделать вывод, что средняя квадратичная погрешность характеризует точность отдельного измерения, в дальнейшую же обработку должна идти величина характеризующая точность вероятнейшего значения a вер.
|
|
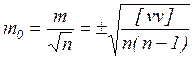
m 0пред =3 m 0
Из формулы (13) видно, что с увеличением числа измерений в n раз значение СКП вероятнейшего значения m 0 уменьшается лишь в 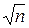 раз, поэтому нет смысла для повышения точности вероятнейшего значения чрезмерно увеличивать число наблюдений. Следует повышать качество самих измерений. Оптимальное число измерений 7-9, хотя это и не всегда удаётся.
раз, поэтому нет смысла для повышения точности вероятнейшего значения чрезмерно увеличивать число наблюдений. Следует повышать качество самих измерений. Оптимальное число измерений 7-9, хотя это и не всегда удаётся.
Разберём всё вышесказанное на примере.
Пример
Получена серия из 9 измерений секстаном горизонтального угла.
ОС 36°18,7′ 36°18,3′ 36°16,8′ 36°19,4′ 36°17,6′ 36°18,2′ 36°19,7′ 36°16,0′ 36°16,9′
Рассчитать:
· вероятнейшее значение горизонтального угла;
· СКП одного (любого) измерения двумя способами;
· предельную погрешность одного измерения;
· СКП вероятнейшего значения;
· предельную погрешность вероятнейшего значения
1.Составляем расчётную таблицу, в первой колонке которой серия измерений, во второй уклонения, в третьей квадраты уклонений.
В первой колонке рассчитываем вероятнейшее значение горизонтального угла, в последней сумму квадратов уклонений.
| OC | v | v v | |
| 36° | 18.7′ | 0.7 | 0.49 |
| 36 | 18.3 | 0.3 | 0.09 |
| 36 | 16.8 | -1.2 | 1.34 |
| 36 | 19.4 | 1.4 | 1.96 |
| 36 | 17.6 | -0.4 | 0.16 |
| 36 | 18.2 | 0.2 | 0.04 |
| 36 | 19.7 | 1.7 | 2.89 |
| 36 | 16.0 | -2.0 | 4.00 |
| 36 | 16.9 | -1.1 | 1.21 |
| OCср 36°18.0′ | 0,0 | [v v]12.18 | |
2. Рассчитываем СКП и предельную погрешность одного измерения:
методом внутренней сходимости по формуле (9):
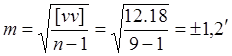
m пред = 3 m = 3.6′
методом размаха:
ОС max =36°19,7′
ОС min =36°16,8′
R = 2,9′
kn = 0.337
m = knR = ±1,1′
3. Рассчитываем СКП и предельную погрешность вероятнейшего значения по формулам (13), (14):
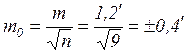
m 0пред = 3*0,4′ = ±1,2′
Контролем результата служит равенство нулю суммы отклонений v.
Все задания выполнены.
1.1.2 Обработка результатов неравноточных измерений навигационных параметров
Ходовой мостик современного судна оснащён различными по принципу действия техническими средствами. Этим обеспечивается возможность измерения одного и того же навигационного параметра с помощью нескольких приборов. Нередко один и тот же параметр измеряется хоть и одним прибором, но в различных условиях или различными людьми. Во всех таких случаях точность результатов будет неодинаковой, такие измерения называют неравноточными или неравновесными. Для сравнения неравноточных измерений пользуются величинами называемыми весами.
Вес p характеризует степень доверия к данному измерению (серии измерений) по сравнению с другими измерениями (сериями). Например, степень доверия к измерениям выполненным старым морским волком, поросшим в нижней части ракушками, будет значительно выше, чем к измерениям сделанным ленивым студентом КМТИ.
Вес p , взятый отдельно, без сопоставления с весами других измерений не несёт никакой информации. Он является сравнительной характеристикой качества наблюдений, и его следует рассматривать совместно с весами других наблюдений.
Принципы, по которым отдельным измерениям приписывают веса, могут быть различными. Например если результаты измерений ai характеризуются своими СКП mi, то этим измерениям присваивают веса pi, обратно пропорциональные квадратам их СКП:
|
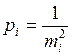
Веса, вычисленные по формуле (16) называют абсолютными.
Как уже говорилось, вес измерения рассматривается совместно с весами других измерений, следовательно, веса, можно умножать на любой коэффициент, естественно коэффициент должен быть одинаков для всей серии, в этом случае соотношение весов не изменяется, а вес называется относительным.
|
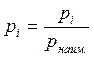
хотя и нередко наоборот, что бы наибольший вес был равен единице (в этом случае все веса делят на наибольший вес)
|
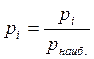 .
.
|
pi = ni ,
|
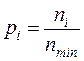
хотя этот принцип менее обоснован, чем предыдущий.
Предположим, что в результате измерений некоторого навигационного параметра получен ряд значений а1, a 2 ... an с весами p 1 , p 2 … pn. За вероятнейшее значение ряда неравновесных измерений принимается весовое среднее или весовая арифметическая середина:
|
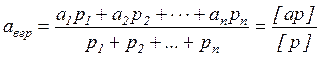
При неравноточных измерениях критерием точности служит СКП m, того измерения, вес которого принят за единицу. Эта погрешность называется СКП единицы веса. Вычисляется СКП единицы веса по формуле подобной (9) и является её обобщением:
|
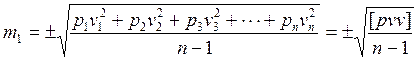
В случае если a ист известно:
|
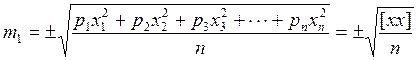
СКП mpi отдельного измерения ai имеющего вес pi, вычисляется по формуле:
|
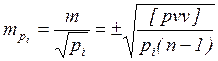
В конце концов наибольший интерес представляет формула для СКП весового среднего a вер, являющаяся венцом обработки ряда неравновесных измерений:
|
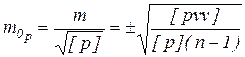
Предельная СКП mp пред весового среднего вычисляется по формуле:
|
|
и mp пред = t m 0 p,
для случая с ограниченным числом наблюдений, где t коэффициент выбираемый из Таблицы 3. Методика обработки при помощи доверительных оценок подробно разбиралась в предыдущем параграфе.
Пример 1
Дано: серия из шести пеленгов ИП измеренных с разной точностью и соответствующие им СКП.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| ИП | 315.6 | 315.4 | 316.2 | 316.1 | 316.2 | 315.6 |
| mип | 0.4° | 0.7° | 1.2° | 0.8° | 0.6° | 0.9° |
Найти:
1. Веса каждого измерения.
2. Вероятнейшее значение измеренного параметра.
3. СКП единицы веса.
4. СКП вероятнейшего значения и оценить его доверительной оценкой с надёжностью 0.99.
Решение:
- Составляем расчётную таблицу:
· в первую колонку вносим серию измерений;
· во второй колонке рассчитываем веса измерений по формуле (18), за коэффициент k принимаем квадрат значения наибольшего СКП m ип m a x =1.2° (третье измерение) k =(1.2)2=1.44
и находим сумму весов [ p ]=21
· в третьей колонке рассчитываем произведения квадратов уклонений v 2 на соответствующие веса и находим сумму этих произведений [ pvv ]=1.93;
| ИП | p | ИП*p | v | pv2 |
| 315.6 | 9.0 | 2840.4 | -0.2 | 0.27 |
| 315.4 | 2.9 | 926.9 | -0.4 | 0.41 |
| 316.2 | 1.0 | 316.2 | 0.4 | 0.19 |
| 316.1 | 2.3 | 711.2 | 0.3 | 0.25 |
| 316.2 | 4.0 | 1264.8 | 0.4 | 0.76 |
| 315.6 | 1.8 | 561.1 | -0.2 | 0.05 |
|
| 21.0 | 6620.6 | [pvv] 1.93 | |
· Рассчитываем вероятнейшее значение по формуле (20).
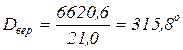
- Рассчитываем СКП единицы веса по формуле (21):
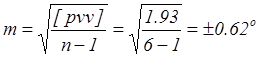
- Рассчитываем СКП и предельную погрешность вероятнейшего значения с заданной надёжностью по формулам (24) и (25):
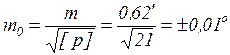
при a = 0,99, по таблице 3 t =4.03
m 0пред = 4.03*0.01′ = ±0.04°
Истинное значение ИПист находится в интервале от 315,76° до 315,84°.
1.2 Расчеты погрешностей навигационных параметров
изменяющихся во времени и определение доверительных оценок
1.2.1 Обработка серии измерений навигационных параметров изменяющих своё значение с течением времени
Большинство измерений навигационных параметров судоводитель производит с движущегося судна в течение некоторого промежутка времени. За это время, судно успевает изменить своё положение относительно измеряемого объекта. То есть каждое последующее измерение, должно отличаться от предыдущего. Если характер изменения навигационного параметра близок к линейному, а промежуток времени между измерениями небольшой, то на вероятнейшем значении измеряемой величины это практически не скажется (значения большие и меньшие средней величины взаимокомпенсируются), а вот на значении СКП измеряемой величины это движение отразится в значительно большей степени.
Один из наиболее характерных случаев – измерение высоты светила навигационным секстаном с движущегося судна. При движении судна, как мы уже говорили, наблюдатель меняет своё положение относительно объекта наблюдения, т.е. в данном случае изменяется зенит наблюдателя, помимо этого в промежуток времени между наблюдениями светило меняет своё положение на небесной сфере.
Для приведения измеренных высот к одному моменту служит поправка D hT. Рассчитывается поправка следующим образом:
· в таблице 17 МТ-75 (таблица 15-б МТ-63) выбирается поправка D hT 10 – изменение высоты светила за 10 секунд или в таблицах МТ-63 таблица 15-а поправка D hT 1 – изменение высоты светила за 1 минуту. Вход в таблицы по широте j и азимуту на светило А.
· если светило находится в восточной части горизонта - поправка положительна, в западной – отрицательна.
· Умножив D hT 1 на прошедшее время в минутах D T м получим D hT
D hT = D T м D hT 1
Для приведения измеренных высот к одному зениту служит поправка D hz . Рассчитывается поправка следующим образом:
· В таблице 16 МТ-75 (МТ-63) выбирается поправка D hz – изменение высоты светила за 1 минуту плавания. Вход в таблицу по скорости V и курсовому углу светила (КУ = А – ПУ). Если КУ<90° поправка положительна, КУ>90° отрицательна. Если нет дрейфа и течения, вместо ПУ берётся ИК.
· Умножив D hz 1 на прошедшее время в минутах D T м получим D hz
D hz = D T м D hz 1
Совместная поправка D h = D hT + D hz или D h = D T м ( D hT 1 + D hz 1 ).
При этом D hT 1 = 6* D hT 10 .
Работа с поправкой D hT 10 возможна и в секундах. В этом случае, получаем временной коэффициент делением времени выраженного в секундах на десять. Поправка, выраженная в секундах, получается умножением D hT 10 на полученный коэффициент: 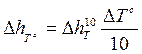
1.2.2 Определение с заданной надёжностью доверительных оценок измеряемой величины и её СКП
Хотим подчеркнуть, что методика обработки измерений описанная в предыдущих параграфах, не совсем обоснована, т.к. формулы (9)-(14) выведены в предположении, что число измерений n очень велико. В частности при расчёте предельного значения мы априори брали коэффициент равный 3 и получали вероятность P =0.997, что верно только при n → ∞. На практике же это число конечно и весьма ограничено. Поэтому возникает важная задача оценки точности величин a вер, m , m 0 при конечном и ограниченном числе n.
Другими словами требуется установить вероятность P = a того, что при заданном конечном числе измерений n неизвестное значение a ист заключено в границах a вер – m 0пред до a вер + m 0пред. Эти границы называют доверительными, а интервал a вер ± m 0пред доверительным интервалом с заданной надёжностью a = P. Таким образом, нам известны n, a вер и задано m 0пред. Найти: a.
Обратная задача формулируется следующим образом: каким при заданном числе измерений n должен быть доверительный интервал, для того, чтобы с заданной надёжностью a можно было утверждать, что неизвестная величина a ист не выйдет за границы доверительного интервала:
a вер – m 0пред < a ист < a вер + m 0пред
То есть, нам известны n, a вер и задано a. Найти: m 0пред
Решение этой задачи в обоих постановках достигается при помощи распределения Стьюдента. Оно учитывает ограниченность числа измерений n и при условии n→ ∞ переходит в нормальное распределение. На его основе составлена Таблица 3. связывающая число наблюдений n, надёжность a и коэффициент 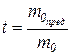 , выносимый в формулу (11). В этом случае формула (11) приобретает вид: m 0пред = t m 0
, выносимый в формулу (11). В этом случае формула (11) приобретает вид: m 0пред = t m 0
Таблица 3. Значения коэффициента t по заданным n и a.
| a n | 0.5 | 0.7 | 0.8 | 0.9 | 0.95 | 0.99 | 0.999 |
| 3 | 0.82 | 1.39 | 1.89 | 2.92 | 4.30 | 9.92 | 31.60 |
| 4 | 0.76 | 1.25 | 1.64 | 2.35 | 3.18 | 5.84 | 12.92 |
| 5 | 0.74 | 1.19 | 1.53 | 2.13 | 2.78 | 4.60 | 8.61 |
| 6 | 0.73 | 1.16 | 1.48 | 2.02 | 2.57 | 4.03 | 6.87 |
| 7 | 0.72 | 1.13 | 1.44 | 1.94 | 2.45 | 3.71 | 5.96 |
| 8 | 0.71 | 1.12 | 1.41 | 1.89 | 2.36 | 3.50 | 5.41 |
| 9 | 0.71 | 1.11 | 1.40 | 1.86 | 2.31 | 3.36 | 5.04 |
| 10 | 0.70 | 1.10 | 1.38 | 1.83 | 2.26 | 3.25 | 4.78 |
| 12 | 0.70 | 1.09 | 1.36 | 1.80 | 2.20 | 3.11 | 4.44 |
| 14 | 0.69 | 1.08 | 1.35 | 1.77 | 2.16 | 3.01 | 4.22 |
| 16 | 0.69 | 1.07 | 1.34 | 1.75 | 2.13 | 2.95 | 4.07 |
| 20 | 0.69 | 1.07 | 1.33 | 1.73 | 2.09 | 2.86 | 3.88 |
| 60 | 0.68 | 1.05 | 1.30 | 1.67 | 2.00 | 2.66 | 3.46 |
| 120 | 0.68 | 1.04 | 1.29 | 1.66 | 1.98 | 2.62 | 3.37 |
| ∞ | 0.67 | 1.04 | 1.28 | 1.64 | 1.96 | 2.58 | 3.29 |
Примерно также решается вопрос и об оценке точности определения СКП единичного измерения, если число измерений конечно и ограничено.
На основе распределения Пирсона с заданной надёжностью a утверждается, что истинное значение СКП единичного измерения m ист отличается от вычисленного не более чем на величину e.
На основе этого распределения составлена Таблица., связывающая число наблюдений n, надёжность a и коэффициент 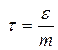 . То есть выбрав из таблицы 4 коэффициент t и рассчитав величину e = t ∙ m c надёжностью a можно утверждать, что m – e < m ист < m + e.
. То есть выбрав из таблицы 4 коэффициент t и рассчитав величину e = t ∙ m c надёжностью a можно утверждать, что m – e < m ист < m + e.
Или наоборот, зная величину e можно определить надёжность a.
Таблица.4. Значения коэффициента t по заданным n и a.
| a n | 0.5 | 0.7 | 0.8 | 0.9 | 0.95 | 0.99 | 0.999 |
| 5 | 0.25 | 0.40 | 0.56 | 0.95 | 1.37 | 2.67 | 5.64 |
| 6 | 0.22 | 0.35 | 0.48 | 0.79 | 1.09 | 2.01 | 3.88 |
| 7 | 0.20 | 0.32 | 0.41 | 0.65 | 0.92 | 1.62 | 2.98 |
| 8 | 0.18 | 0.29 | 0.38 | 0.58 | 0.80 | 1.38 | 2.42 |
| 9 | 0.17 | 0.27 | 0.35 | 0.52 | 0.71 | 1.20 | 2.06 |
| 10 | 0.16 | 0.25 | 0.33 | 0.49 | 0.65 | 1.08 | 1.80 |
| 12 | 0.15 | 0.23 | 0.30 | 0.43 | 0.55 | 0.90 | 1.45 |
| 14 | 0.14 | 0.21 | 0.28 | 0.38 | 0.48 | 0.78 | 1.23 |
| 16 | 0.13 | 0.19 | 0.26 | 0.35 | 0.44 | 0.70 | 1.07 |
| 18 | 0.12 | 0.18 | 0.24 | 0.32 | 0.40 | 0.63 | 0.96 |
| 20 | 0.11 | 0.17 | 0.22 | 0.29 | 0.37 | 0.58 | 0.88 |
| 100 | 0.05 | 0.07 | 0.09 | 0.12 | 0.14 | 0.20 | 0.27 |
Пример 2
В широте j = 36.5°N судно следует ИК = 114° со скоростью V = 16 уз. Измерена серия 7 высот светила, азимут которого А=60,7° SOst.
Моменты наблюдения Ti и отсчёты секстана ОСi приведены в таблице.
| Ti | 10ч57м13с | 10 57 58 | 10 58 48 | 10 59 35 | 11 00 27 | 11 01 10 | 11 02 02 |
| ОС i | 29°46,7′ | 55.5′ | 30°04,8′ | 12,0′ | 20,8′ | 29,0′ | 39,5′ |
Задание:
1. привести ОСi к одному зениту и моменту времени.
Рассчитать:
2. вероятнейшее значение высоты светила;
3. СКП единичного измерения двумя способами;
4. предельную погрешность единичного измерения;
5. доверительный интервал накрывающий истинное значение СКП единичного значения с надёжностью (вероятностью) 0,90.
6. надёжность a определения СКП для доверительного интервала в 0,5 единицу измеряемого параметра (±0,5′)
7. СКП вероятнейшего значения;
8. предельную погрешность вероятнейшего значения измеренной величины и доверительный интервал накрывающий истинное значение измеряемой величины с надежностью (вероятностью) 0,95.
9. надёжность a для доверительного интервала в одну единицу измеряемого параметра (±1′).
Решение:
· Составляем расчётную таблицу, в первую колонку вносим моменты наблюдений, в пятую отсчёты секстанов.
| 1 | 2 |
| 3 | 4 | 5 | 6 | 7 | 8 | ||||
| Ti | DTi |
| DTi | DhT+Dhz | OСi | OCпр | vi | vi2 | ||||
| 10ч | 57м | 13с | 2м | 22с | 2.37м | 25.5′ | 29° | 46.7′ | 30° | 12.2′ | -0.2 | 0.04 |
| 10 | 57 | 58 | 1 | 37 | 1.62 | 17.4 | 29 | 55.5 | 30 | 12.9 | 0.5 | 0.25 |
| 10 | 58 | 48 | 0 | 47 | 0.78 | 8.4 | 30 | 4.8 | 30 | 13.2 | 0.8 | 0.64 |
| 10 | 59 | 35 | 0 | 0 | 0.00 | 0.0 | 30 | 12.0 | 30 | 12.0 | -0.4 | 0.16 |
| 11 | 0 | 27 | 0 | -52 | -0.87 | -9.3 | 30 | 20.8 | 30 | 11.5 | -0.9 | 0.81 |
| 11 | 1 | 10 | -1 | -35 | -1.58 | -17.1 | 30 | 29.0 | 30 | 11.9 | -0.5 | 0.25 |
| 11 | 2 | 2 | -2 | -27 | -2.45 | -26.4 | 30 | 39.5 | 30 | 13.1 | 0.7 | 0.49 |
|
|
|
|
|
|
|
|
|
| ОС=30°12.4′ | 0.0 | Sv22.64 | |
· Выбираем момент времени T0 к которому будем приводить все измерения серии, чаще всего это или средний, или последний момент. Возьмём средний момент времени, в нашем случае четвёртый, т.е. T0 = T4.
· Рассчитываем промежутки времени D Ti между T0 и текущим моментом Ti, D Ti = T 0 – Ti и вносим результаты во вторую колонку. В третью колонку внесём те же промежутки D Ti, но секунды выразим в десятых долях минуты.
· Рассчитаем поправки для приведения высоты светила к одному моменту и к одному зениту:
из таблицы 17 МТ-75 по широте j и азимуту на светило А
D hT 10 = +1,75′; D hT 1 = 6*1,75′=10,50′.
Из таблицы 16 МТ-75(63) по скорости V = 16 уз и КУ=119,3°– 114° =5,3°
D hz 1 = +0,27.
Рассчитываем совместную поправку за 1 минуту:
D h 1 = D hz 1 + D hT 1 =10,77
· Рассчитываем произведения D hi = D Ti D h 1, результаты вносим в четвёртую колонку.
· В шестой колонке рассчитываем приведенные отсчёты секстана
ОСпр i = D hi + OCi
· Находим вероятнейшее значение ОС на T0 (четвёртый момент времени) – внизу колонки среднее арифметическое от ОСпр I.
· Рассчитываем СКП:
(методом внутренней сходимости)
В последние две колонки вносим уклонения vi и квадраты уклонений vi 2 соответственно. Внизу колонок находим сумму уклонений и сумму квадратов уклонений.
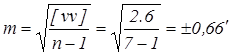
(методом размаха)
ОС max =30°13.2′
ОС min =30°11.5′
R = 1.7′
kn = 0.370
m = knR = ±0.63′
Предельная погрешность единичного измерения m пред = 3 m = 2.0′
· Находим доверительный интервал единичного измерения,
по известному количеству наблюдений n = 7 и заданному в условии a = 0,90 из Таблица. находим значение коэффициента t = 0,65.
Рассчитываем e = t ∙ m = 0.65∙0.66′ = 0.44′
Находим m - e =0,22 и m + e =1,1 следовательно 0,22≤ mист≤1.1.
· Рассчитываем надёжность a для заданного доверительного интервала m ± e в примере e = 0.5 ′.
находим t=e / m=0.75
обратным входом в Таблица. по n =7 измерениям и по известному t =0.75 получаем надёжность a > 0.9.
· Рассчитываем СКП вероятнейшего значения:
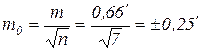
· Находим предельную погрешность вероятнейшего значения и доверительный интервал:
по известному количеству наблюдений n = 7 и заданному в условии a = 0,95 из Таблицы 3 находим значение коэффициента t = 2.45.
m 0пред = tm 0 =2,45∙0.25′ 0.6′ следовательно 30°11,8′≤ ОСист≤30°13,0′.
· Рассчитываем надёжность a для заданного m 0пред = ± 1′
рассчитываем t= m 0пред / m 0 =4
для чего, обратным входом в Таблицу 3 по n =7 измерениям и по найденному t получаем надёжность a >0.99
1.3 Обработка статистических данных методами
линейной корреляции
В практике часто бывают случаи, когда измеренные параметры входят в какую-либо расчётную формулу, причём зачастую сразу несколько параметров. Встаёт вопрос, каким образом определить СКП результата.
Предположим, что какая-либо величина z является функцией некоторого количества различных навигационных параметров x 1 , x 2 ,… xn ,
z = f ( x 1 , x 2 ,… xn );
каждый из которых имеет среднюю квадратичную погрешность mxi, тогда формула для расчёта mz будет иметь вид:
|
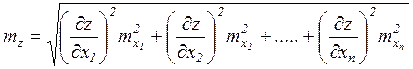
В общем случае по формуле (15) рекомендуется следующий порядок расчётов:
1. Рассчитывают по исходной формуле значение определяемой величины.
2. Рассчитывают частные производные по переменным (измеренным) величинам.
3. Преобразовывают общую формулу СКП для конкретного случая.
4. В рабочую формулу подставляют исходные значения и рассчитывают СКП mz.
Предположим, что мы произвели одновременные измерения двух серий величин x и y . Разумеется, эти измерения были подвержены влиянию случайных ошибок. Как уже говорилось выше, причины возникновения случайных ошибок многочисленны и практически не поддаются учёту. Среди них могут быть ошибки, выражающие некоторую неизвестную нам закономерность, или ошибки, одновременно влияющие на обе величины. То есть эти серии измерений уже нельзя считать независимыми друг от друга. С другой стороны, сказать, что они связаны жёсткой функциональной зависимостью вида y = ax + b, тоже нельзя. В нашем случае взаимосвязь является статистической, т.е. при изменении величины x величина y имеет тенденцию также изменяться.
Эта тенденция соблюдается лишь в большей или меньшей степени, а в каждом конкретном случае возможны отклонения от неё. Зависимость в таких случаях называется корреляционной и характеризуется коэффициентом корреляции r (-1 ≤ r ≤ 1). Если r >0, то большим значениям x в среднем соответствуют большие значения y и наоборот. Чаще всего эта тенденция носит линейный характер. Если r =±1, то зависимость становится функциональной. При r <|0.2| можно считать, что величины не коррелированны.
Стоит заметить, что разговор в этой главе идет о наиболее частом случае корреляции – линейной корреляции. В случае корреляционной зависимости более высоких порядков (гиперболическая, параболическая) зависимости для коэффициента линейной корреляции могу не выполняться, а сам коэффициент рассчитывается более сложным образом.
Численное значение коэффициента r можно найти из специально организованных наблюдений. В штурманской практике нередко возникает необходимость учёта корреляционной зависимости при решении ряда навигационных задач, в первую очередь в вопросах оценки точности обсервации.
Для определения коэффициента корреляции необходимо измерить при более или менее идентичных условиях n парных значений двух навигационных параметров xi и yi (например, два пеленга береговых ориентиров). После определённой статистической обработки данных коэффициент корреляции рассчитывается по формуле:
|
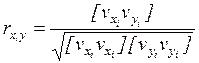 ,
,
где vxi и vyi уклонения величин xi и yi от вероятнейших значений соответственно.
Сама зависимость будет задаваться уравнением линейной регрессии:
|
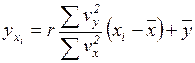 ,
,
где 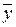 и
и 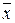 вероятнейшие значения измеряемых величин.
вероятнейшие значения измеряемых величин.
Смысл уравнения линейной регрессии можно выразить так, каждому значению xi с наибольшей вероятностью будет соответствовать значение yxi.
Теперь обратимся к такому важному случаю, когда некоторая искомая величина a определяется, как функция непосредственно измеряемых величин x , y: a=f(x, y).
Предположим, что величины x , y коррелированны, т.е. если налицо взаимная зависимость случайных ошибок в аргументах x и y , в этом случае, СКП величины a определяется следующим образом:
|
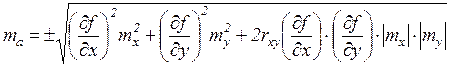
В случае отсутствия корреляционной связи между величинами x и y, формула (30) примет вид (15).
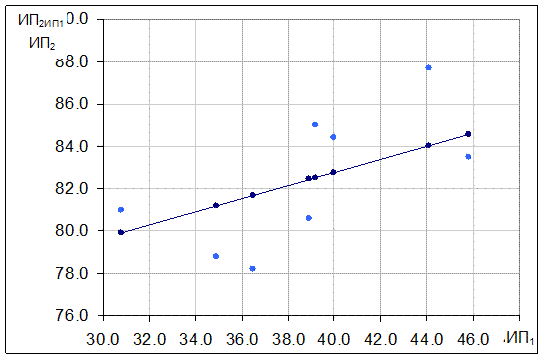
Пример: Дано: две серии пеленгов ИП1, ИП2.
| ИП1 | 30.8° | 34.9° | 36.5° | 39.2° | 38.9° | 40.0° | 45.8° | 44.1° |
| ИП2 | 81.0° | 78.8° | 78.2° | 85.0° | 80.6° | 84.4° | 83.5° | 87.7° |
Найти:
1. вероятнейшие значения измеренных величин;
2. коэффициент корреляции между пеленгами;
3. составить уравнение линейной регрессии, построить график;
4. СКП каждого навигационного параметра;
5. рассчитать вероятнейшее значение горизонтального угла a;
6. рассчитать СКП вероятнейшего значения горизонтального угла a.
Решение:
1. Составляем расчётную таблицу:
1. во вторую и восьмую колонку вводим ИП2 и ИП1 соответственно и рассчитываем вероятнейшее значение (среднее арифметическое) каждой величины;
2. в третьей и седьмой колонках рассчитываем соответствующие уклонения вышеперечисленных величин;
3. в четвёртой и шестой колонках квадраты уклонений;
4. в пятой их произведения;
5. внизу 4 – 6 колонок находим их суммы.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| n | ИП2 | v ип2 | v 2 ип2 | v ип2* v ип1 | v 2 ип1 | v ип1 | ИП1 |
| 1 | 81.0 | 1.4 | 2.0 | 11.2 | 63.6 | 8.0 | 30.8 |
| 2 | 78.8 | 3.6 | 13.0 | 14.0 | 15.0 | 3.9 | 34.9 |
| 3 | 78.2 | 4.2 | 17.6 | 9.6 | 5.2 | 2.3 | 36.5 |
| 4 | 85.0 | -2.6 | 6.8 | 1.1 | 0.2 | -0.4 | 39.2 |
| 5 | 80.6 | 1.8 | 3.2 | -0.2 | 0.0 | -0.1 | 38.9 |
| 6 | 84.4 | -2.0 | 4.0 | 2.4 | 1.5 | -1.2 | 40.0 |
| 7 | 83.5 | -1.1 | 1.2 | 7.7 | 49.4 | -7.0 | 45.8 |
| 8 | 87.7 | -5.3 | 28.1 | 28.2 | 28.4 | -5.3 | 44.1 |
|
| 82.4 | S | 75.86 | 73.95 | 163.2 |
| 38.8 |
2. По формуле (28) находим коэффициент корреляции:
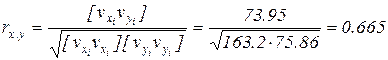
3. Составляем уравнение линейной регрессии
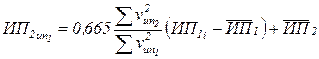
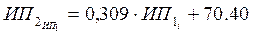
| ИП1 |
|
| 30.8 | 79.9 |
| 34.9 | 81.2 |
| 36.5 | 81.7 |
| 39.2 | 82.5 |
| 38.9 | 82.4 |
| 40.0 | 82.8 |
| 45.8 | 84.6 |
| 44.1 | 84.0 |
Строим зависимость 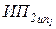 от ИП1
от ИП1
4. По формуле (9) рассчитываем СКП единичных значений
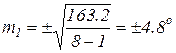 ;
;
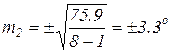
и формуле (13) СКП вероятнейших значений пеленгов.
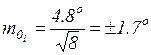
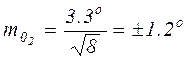
5. Рассчитываем значение горизонтального угла a.
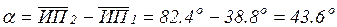
6. Рассчитываем СКП горизонтального угла a
6. без учёта корреляционной зависимости по формуле (15);
Находим частные производные пеленгов:
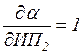 ;
; 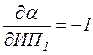
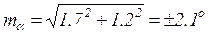
7. и с учётом корреляционной зависимости по формуле (29)
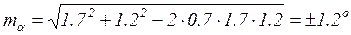
РАЗДЕЛ 2
СПОСОБЫ ОПРЕДЕЛЕНИЕ МЕСТА СУДНА
2.1 Определение места судна (ОМС) методом изолиний
Во время перехода судоводитель постоянно должен знать местоположение судна, т.е. значение координат широты j и долготы l, эта задача решается ведением счисления и постоянным уточнением места обсервациями.
Геометрические величины, получаемые из наблюдения внешних объектов для определения места судна, называют навигационными параметрами.
Совокупность точек, в которых навигационный параметр сохраняет своё значение постоянным, называется изолинией U навигационного параметра. Изолиния навигационного параметра является функцией координат:
U = f ( j , l ) = const .
Для определения места судна необходимо получить, как минимум два навигационных параметра.
Основными методами определения места судна являются – метод изолиний и обобщённый метод линий положения (ЛП).
Методом изолиний место судна можно определять, как графически, так и аналитически.
При помощи графического способа, место судна определяется непосредственно на карте. Этот способ применяется, когда изолинии имеют простую форму, удобную для нанесения на карту. Графический способ подробно рассматривается в курсе навигации, посему, его рассматривать не будем.
Аналитические способы дают место судна только путём математической обработки навигационных параметров. Математически, эти способы весьма сложны, но при современном развитии вычислительной техники, их использование значительно упрощается.
Задачу опрелеления места судна методом изолиний решают в следующем порядке:
· выполняются измерения навигационных параметров;
· составляются системы уравнений изиолиний измеренных параметров;
· подставляются в систему полученные параметры и система решается относительно j o и l o.
 В обобщённом методе линий положения, навигационные параметры после некоторой математической обработки преобразовываются в унифицированные линии положения, оснванные на использовании величины градиента g и его направления t, после чего графическим способом на карте или планшете определяется место судна.
В обобщённом методе линий положения, навигационные параметры после некоторой математической обработки преобразовываются в унифицированные линии положения, оснванные на использовании величины градиента g и его направления t, после чего графическим способом на карте или планшете определяется место судна.
Если, изолиния показывает постоянное значение навигационного параметра, то градиент показывает направление и величину его изменения, разумеется, градиент всегда направлен перпендикулярно изолинии.
|
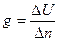 ,
,
то есть показывает, как изменяется навигационный параметр с расстоянием.
Один из простых, но показательных случаев, расчёт градиента глубин. Снимаем разность глубин, на рисунке – D U =10 метров, измеряем расстояние между изолиниями – Dn =0,4 мили, направление градиента идёт по увеличению глубины.
Получение формул для изолиний навигационных параметров, а так же для их градиентов приводятся в курсе лекций, а так же в [1], мы же ограничимся результатами этих выкладок, необходимыми для решения практических задач
Таблица 7.
| Навигационный параметр | Изолиния | Градиент | Направление градиента |
| Локсодромический пеленг с судна на ориентир | 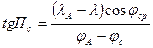
| 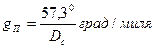
| 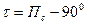
|
| Локсодромический пеленг с ориентира на судно | 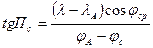
| 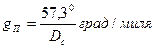
| 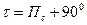
|
| Ортодромический пеленг с ориентира на судно | 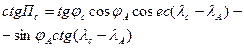
| 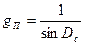 град/миля град/миля
| 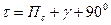
|
| Ортодромический пеленг с судна на ориентир | 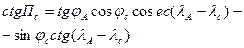
| 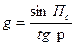 град/миля град/миля
| 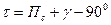
|
| Дистанция на плоскости | 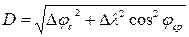
| 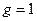 миля миля
| 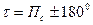
|
| Дистанция на сфере | 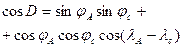
| 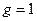 миля миля
| 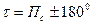
|
| Горизонтальный угол | 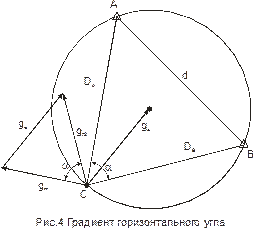
| 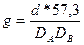 град/миля град/миля
| Снимается графически, направлен из счислимой точки к центру описанной окружности. |
| Вертикальный угол | 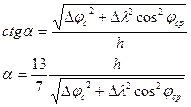
| 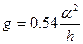
| 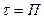
|
| Высота светила | 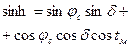
| 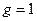 миля миля
| 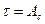
|
В таблице:
j с – счислимая широта
l с – счислимая долгота
j А – широта измеряемого объекта
l А – долгота измеряемого объекта
D А , D В – дистанция до измеряемого объекта
Dc – счислимая дистанция
d – расстояние между ориентирами
Пс – счислимый пеленг
g - сферическое схождение меридианов
Для ортодромического пеленга с судна на ориентир 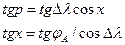
2.2 Графоаналитический метод
Этот метод основан, на обобщённом методе линий положения (ЛП). Суть способа состоит в том, что на коротком отрезке, изолинию сколь угодно сложной формы можно заменить, на прямую, касательную к этой изолинии. Впервые этот метод был применён для определения места судна по наблюдениям светил и проще его пояснить именно на этом примере.
Предположим, что наблюдатель находится в точке М с координатами j и l, которые ему не известны и которые предстоит определить с достаточной точностью. В этой точке он измеряет высоту h светила С.
Зная высоту светила можно провести круг равных высот с радиусом z = 90 ° - h. Разумеется, точка М будет находиться где-то на этой окружности.
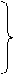 При этом наблюдателю известны счислимые (приблизительные) координаты j С и l С точки. Из параллактического треугольника можно рассчитать счислимые высоту и азимут светила:
При этом наблюдателю известны счислимые (приблизительные) координаты j С и l С точки. Из параллактического треугольника можно рассчитать счислимые высоту и азимут светила:
|
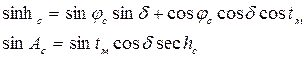
 Эту высоту наблюдатель измерил бы, если б находился в точке МС. Через эту точку так же можно провести круг равных высот с радиусом z С = 90 ° - h С. Разность n = h – hC даст нам расстояние в милях между действительным и счислимым кругами равных высот. Проведя азимут АС на светило и отложив на нём со своим знаком расстояние n, мы найдём определяющую точку К на действительном круге равных высот. Проведя через неё перпендикуляр, мы получим Высотную Линию Положения (ВЛП).
Эту высоту наблюдатель измерил бы, если б находился в точке МС. Через эту точку так же можно провести круг равных высот с радиусом z С = 90 ° - h С. Разность n = h – hC даст нам расстояние в милях между действительным и счислимым кругами равных высот. Проведя азимут АС на светило и отложив на нём со своим знаком расстояние n, мы найдём определяющую точку К на действительном круге равных высот. Проведя через неё перпендикуляр, мы получим Высотную Линию Положения (ВЛП).
Измерив высоту другого светила и произведя аналогичные расчёты, мы получим вторую ВЛП. Пересечение обоих ВЛП даст нам обсервованное место судна М0.
Учитывая то, что радиус круга равных высот, как правило, на несколько порядков больше расстояния между точками МС и М, замена дуги на прямую линию практически не отразится на точности расчётов. То есть мы можем считать, что полученная нами точка М0 практически совпадёт с действительной точкой М.
Переходя к обобщённому методу линий положения можно сказать, что навигационным параметром U, является истинная высота светила h, градиент g при этом равен единице, направление градиента совпадает с азимутом на светило.
Обобщённый порядок расчётов при графоаналитическом способе выглядит следующим образом:
1. Измеряются навигационные параметры U о 1 и U о 2;
2. рассчитываются счислимые параметры U с 1 и U с 2 (по формулам приведенным в таблице),на моменты измерений U о 1 и U о 2;
3. вычисляются разности
DU 1= U о 1 - U с 1 ; DU 2= U о 2 - U с 2;
4. рассчитываются модули g 1 и g 2 градиентов навигационных параметров и их направления t 1 и t 2;
5. по формулам
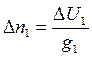 ;
; 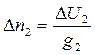
рассчитываются переносы;
6. на карте или планшете от счислимой точки по элементам t 1 , D n 1 и Dt 2 , n 2 строятся линии положения I–I и II–II, делается єто следующим образом:
1. Через счислимую точку при помощи транспортира проводится направление градиента t 1 первого навигационного параметра.
2. Вдоль направления градиента откладывается перенос n1 по направлению, если перенос положителен, в противоположном – если отрицателен.
3. Через полученную точку жирным цветом проводится линия положения, обозначаемая с концов римской цифрой I.
4. Для построения второй линии положения производятся действия 1-3.
5. Пересечение высотных линий положения даёт нам обсервованную точку.
6. Снимаем координаты точки и невязку.
7. Производим оценку точности обсервованного места.
Следует учитывать, что производя построения на планшете, мы снимаем с него приращение координаты D j , и отшествие Dw, далее при помощи углового масштаба, или формулы получаем приращение Dl .
При аналитическом методе п.6, графических расчётов заменяется совместным решением системы уравнений:
|
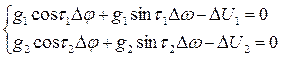
где - Dw отшествие.
Решив эту систему методом определителей и учитывая, что
Dl=Dw/ cos ( j c ),
получим приращения координат:
|
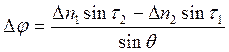
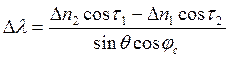 ,
,
где Q = t 2 - t 1
далее определяем искомые координаты:
j 0 = j с + D j : l 0 = l с + D l .
Как уже отмечено выше, метод ЛП основывается на замене изолинии навигационного параметра, могущего иметь совершенно разные формы, на отрезок прямой, направленный по касательной к изолинии. Естественно такая замена возможна лишь на небольших расстояниях, как правило, не превышающих 15-20 миль в приращениях координат. При получении приращений с большими значениями полученное место следует принять за первое приближение, а полученные координаты за счислимые и повторить расчёты ещё раз.
2.3 Влияние случайных ошибок измерений
на точность места, определяемого по двум ЛП
2.3.1 Смещение и вес ЛП
Ошибки в измерениях навигационного параметра к ошибкам в изолиниях, а значит, и в ЛП, которые их заменяют. Навигационные параметры по которым строятся изолинии и ЛП, могут получаться совершенно разными способами и иметь величины ошибок имеющих разные размерности и величины, учитывая это для унификации удобно применять среднеквадратическое смещение ЛП равное
|
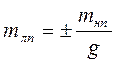 , где
, где
m нп – СКП навигационного параметра,
g – его градиент
Она показывает, на сколько линейных единиц смещается ЛП при заданной величине СКП. Величину m нп называют смещением ЛП или полосой ЛП, т.к. при изменении абсолютного значения Uo, на величину ± m нп провести соответствующие этим значениям U '= Uo – m нп U ''= Uo + m нп границы, которые определят среднеквадратическую полосу положения. Вероятность поподания истинного сначения в эту полосу определяется вероятностью погрешности навигационного параметра, для СКП ~ 0.67, для предельной СКП ~ 0.997, более подробно об этом говорилось ранее.
При оценке точности рассматривается вероятность попадания истинного места судна в пределы фигуры ошибок, а не отклонения или ошибки от истинного места судна. Теоретически необходимо рассматривать вероятность того, что фигура погрешности данной формы и площади данного размера, расположенная в данном месте накроет точку истинного места. Практически рассматривают отклонение, полагая центр фигуры вероятнейшим местом. На практике считают, чтобы погрешности измерения параметров распределены беспрерывно, т.е. мест судна бесконечно много.
Для оценки точности места судна в судовождении применяют: эллипсы и круги погрешностей.
2.3.2 Эллипс погрешностей
При ОМС составляется и решается уравнение, прокладывается изолиния или ЛП отягощенная ошибками измерений. Величины и знаки истинных ошибок измерений носят случайный характер, и учесть их можно лишь статистически.
Вывод формул оценки точности места базируется на предположениях:
1) Грубые ошибки или промахи, пропущенные при измерениях, исключены.
2) Компенсированы систематические ошибки измерений
3) Ошибки вычислений и графики малы и несущественны
4) Случайные ошибки измерения подчинены нормальному закону распространения случайных величин.
 Достоинства оценки места судна эллипсом.
Достоинства оценки места судна эллипсом.
1) Он имеет строго теоретическое обоснование.
2) Это единственная кривая, во всех точках которой плотность вероятности ошибки постоянна.
3) Вероятность попадания истинного места судна в область, ограниченную эллипсом, больше, чем у любой другой фигуры одинаковой с эллипсом площади.
4) Эллипс дает рассеяние мест судна по направлениям.
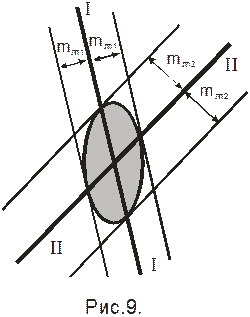
При двух ЛП на практике, достаточно вписать приближенный эллипс в четырёхугольник, образованный полосами погрешностей. При этом вероятнейшим местом судна будет точка пересечения ЛП - центр эллипса погрешностей из-за того, что в элементарно малых окрестностях этой точки вероятность нахождения места судна больше, чем в аналогичных окрестностях любой другой точки.
Для строгого построения эллипса погрешностей рассматриваются векториальные ошибки  , линии положения 1 и 2 по направлению ЛП2 и ЛП1.
, линии положения 1 и 2 по направлению ЛП2 и ЛП1.
Учитывая, что вектора  - сопряжённые полуоси эллипса используют теорему Аполлония
- сопряжённые полуоси эллипса используют теорему Аполлония
|
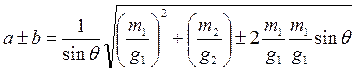
или
|
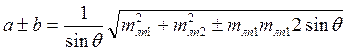 ;
; 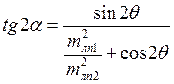
Где a угол, определяющий направление большой полуоси эллипса, который всегда откладывается внутри острого угла Q от более точной ЛП.
Ещё один способ расчета эллипса погрешностей по 2-м ЛП, заключается в использовании таблицы прил. № 5 к МТ-75 Аргументами для входа в таблицу служат величины
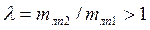
|
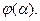 Полуоси рассчитывают по формуле:
Полуоси рассчитывают по формуле:
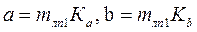
Таблица приложений S составлена по преобразованным формулам Аполлония.
|
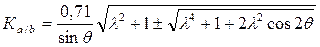 ;
; 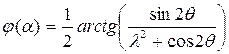
2.4 Графические методы отыскание вероятнейшего места судна
при избыточном числе линий положения
При ОМС по двум ЛП или изолиниям имеет место существенный недостаток, а именно, практически отсутствует возможность проверить наличие систематических ошибок или промахов в измерениях и избавиться от их влияния. Частично эту проблему можно решить, получив избыточное число навигационных параметров, как правило, три или четыре.
Получив три ЛП (изолинии) и нанеся их на карту, вследствие влияния случайных и систематических погрешностей, линии положения сойдутся не в одной точке, а мы получим треугольник погрешностей. К сожалению вычисление промахов, кроме очень крупных практически невозможно, но от воздействия одинаковых систематических ошибок избавиться возможно.
Практически встают следующие вопросы:
· Каким образом лучше выбирать ориентиры?
· Где выбрать обсервованное место судна при равноточных и неравноточных измерениях?
· Как оценить точность полученного места и получить площадь, где находится место судна с наибольшей вероятностью.
2.4.1 Действие систематических ошибок
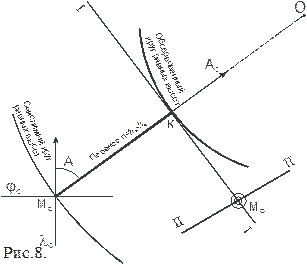
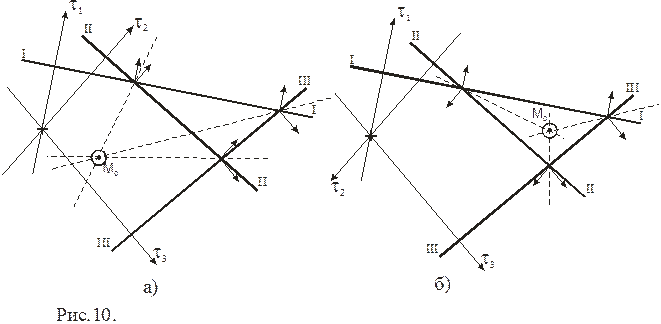
В теоретическом курсе показывается, что если между двумя ЛП положения провести биссектрису угла, то полученная «разностная» линия будет свободна от действия систематических ошибок. Для построения достаточно двух биссектрис. Эту операцию иногда называют «разгоном» треугольника погрешностей.
Для построения биссектрис именно тех углов, при вершинах треугольника перпендикулярно линиям положения, наносятся стрелочки в направлении азимута, затем проводится биссектриса меньшего угла между стрелочками (Рис. 10).
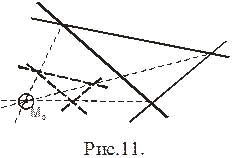 Другой способ разгона треугольника погрешностей заключается в смещении всех ЛП (или изолиний) на одну и ту же величину, в одном направлении. Далее сходные углы соединяются линиями. На пересечении этих линий мы получим место свободное от систематических погрешностей (рис.11).
Другой способ разгона треугольника погрешностей заключается в смещении всех ЛП (или изолиний) на одну и ту же величину, в одном направлении. Далее сходные углы соединяются линиями. На пересечении этих линий мы получим место свободное от систематических погрешностей (рис.11).
При построении биссектрис и определении обсервованного места может встретиться два случая:
Ориентиры расположены в одной половине горизонта, в этом случае точка пересечения биссектрис будет лежать вне треугольника погрешностей (Рис.10 а).
Вследствие того, что в реальных условиях на систематические ошибки накладываются ещё и случайные, приём может привести к грубым ошибкам в обсервованном месте, и его следует применять с большой осторожностью.
Ориентиры расположены в разных частях горизонта. В этом случае точка пересечения биссектрис будет лежать внутри треугольника ошибок(Рис.10 б).
Учитывая то, что внутри треугольника отклонение обсервованной точки от реальной значительно меньше, чем может быть снаружи, для обсервации рекомендуется подбирать ориентиры лежащие в разных частях горизонта.
Следует помнить, что вышесказанное справедливо, лишь при допущении, что действие случайных ошибок равно нулю. Поэтому нельзя считать, что наши построения обнаруживают систематическую ошибку, скорее наоборот, они сами являются следствием предположения, что действуют только равные систематические ошибки.
2.4. 2 Действие случайных ошибок
 Случайные ошибки возникают из-за влияния разнородных факторов, учёт которых невозможен.
Случайные ошибки возникают из-за влияния разнородных факторов, учёт которых невозможен.
В случае если все линии равноточные, а действие систематических ошибок равно нулю, вероятнейшее место будет находиться на пересечении антимедиан треугольника, которая представляет собой зеркальное изображение медианы относительно биссектрисы.
При увеличении треугольника в длину, обсервованное место смещается к более короткой стороне и прямому углу, что соответствует выводам из теории ошибок (чем ближе угол пересечения двух линий положения к 90°, тем вес этой точки больше).
2.4.3 Совместное действие систематических и случайных ошибок
В действительности систематические и случайные ошибки действуют всегда совместно. Исходя из этого, обе категории ошибок необходимо согласовывать так, что бы они не противоречили друг другу.
Следовательно, для трёх линий положения самой выгодной разностью азимутов является 120°.
Ориентиры для наблюдений не следует выбирать в одной половине горизонта, если же по ряду причин место выбрано именно таким образом, то метод биссектрис следует применять с большой осторожностью, желательно после анализа допущенных ошибок.
При выборе ориентиров в разных частях горизонта, вероятнейшее место всегда находится внутри треугольника погрешностей и, как правило, удобнее применять метод антимедиан.
2.4.4 Отыскание вероятнейшего места судна при неравноточных измерениях
В предыдущих параграфах, рассматривался случай обработки серии неравноточных измерений одного и того же навигационного параметра, зачастую приходится рассматривать случай обработки неравноточных измерений различных навигационных параметров, т.е. нескольких ЛП с различными СКП и соответственно весами p. Как уже говорилось ранее вес, это величина, характеризующая степень доверия к данному измерению или линии положения по сравнению с другими измерениями или линиями положения. Следовательно, в фигуре погрешностей состоящей из трёх или четырёх линий вероятнейшее место будет ближе к линии имеющей больший вес и к точкам пересечения линий, угол между которыми, ближе к 90°.
Существует несколько, как графических, так и аналитических способов отыскания вероятнейшего места, при наличии трёх или более, неравноточных ЛП.
Штурманский метод.
|
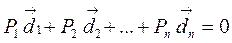 ,где
,где
d 1, d 2, d 3 – перпендикуляры опущенные из вероятнейшего места Кв на соответствующие линии положения.
Порядок действий:
1. Рассчитать абсолютные и относительные веса ЛП и обозначить относительные веса около каждой ЛП.
2. На глаз выбрать точку ближе к более тяжелым ЛП и углам более близким к 90°.
3. Провести из полученной точки перпендикуляры ко всем ЛП, измерить их длину и умножить каждую длину на соответствующий вес.
4. Построить по ним векторную сумму вида  , для этого откладывается из нанесённой точки первый вектор, с длинной равной P 1 d 1 и направлением первого перпендикуляра d 1. Последующие вектора, откладываются из конца предыдущего.
, для этого откладывается из нанесённой точки первый вектор, с длинной равной P 1 d 1 и направлением первого перпендикуляра d 1. Последующие вектора, откладываются из конца предыдущего.
5. Соединить начало и конец построения отрезком прямой, его середину принимают за новое место судна, если длинна полученного отрезка не более 0,5 мили, принимают полученную точку за вероятнейшее место, в противном случае построение повторяют до тех пор, пока отрезок не будет меньше 0,5 мили.
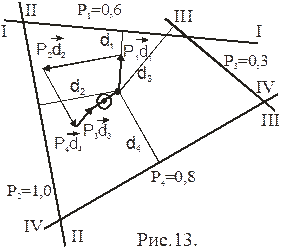
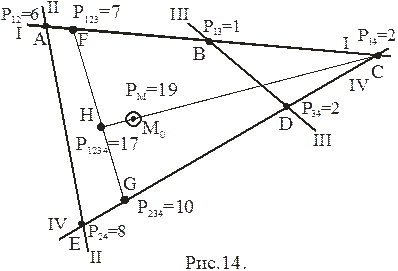
Центрографический метод
Этот метод предполагает последовательное нахождение суммы весов точек пересечения 2-х ЛП и как результат, суммарный вес и вероятнейшее место судна.
1. Рассчитываем абсолютные веса ЛП, затем по формуле:
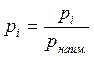
получаем относительные веса и округляем их до целого значения.
2. Получаем углы пересечения ЛП с меридианом b i = t i ± 90°.
3. Получаем углы пересечения ЛП друг с другомQ ij, вычитая из большего значения b i меньшее b j.
4. Определяем веса точек пересечения ЛП Pij по формуле:
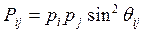
Вес точек пересечения линий положения с небольшим углом рассчитывать не имеет смысла за их малостью.
5. Последовательно получаем веса промежуточных точек, помня о том, что веса использованных точек заменяются совместным весом промежуточной.
Например, на рис.8. вес промежуточной точки F, лежащей на отрезке между точками АВ, равен сумме весов этих точек, а сама точка располагается на расстоянии, обратно пропорциональном весам точек, то есть
lAF = lABP 13 /( P 12 + P 13 ).
Аналогично рассчитывается вес и положение точки G на отрезке ED, вес и положение точки H и точки M 0.
Этот прием удобен для объединения нескольких мест судна, имеющих различную точность, т.е. вместо нескольких, получаем одно вероятнейшее место судна, с новым соответствующим СКП.
Например, при незначительном расхождении между обсервованным и счислимым местами судна их можно заменить вероятнейшим местом, полученным центрографическим методом или штурманским приемом.
Такой метод определения вероятнейшего места судна применяется в корректируемом счислении.
2.4.5 Общий случай построения эллипса погрешностей
1. Определить или выбрать из справочников
2. Рассчитать градиенты g линий положения
3. Рассчитать смещение всех ЛП:
4. Определить абсолютные веса ЛП
5. Найти вероятнейшее место судна центрографическим способом или штурманским приемом. Вероятнейшее место судна – центр эллипса погрешностей.
6. Построить полигон весов.
В свободном месте карты в крупном масштабе строят векторную сумму абсолютных весов под двойными углами 2 b i каждой ЛП к меридиану.
Величина результирующего вектора построения дает величину  в масштабе построения, а его угол с его угол с Nu равен 2 b 0.
в масштабе построения, а его угол с его угол с Nu равен 2 b 0.
Арифметическая сумма даст величину 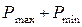
|
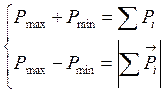
решив систему уравнения полуосей эллипса получим:
|
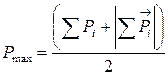 ,
, 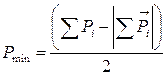
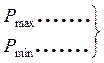 веса полуосей эллипса
веса полуосей эллипса
7.
|
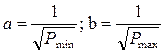
8. Под углом b к Nu c центром в вероятнейшем месте судна построить эллипс погрешностей, который двумя взаимноперпендикулярными ЛП в виде осей эллипса эквивалентен информации всех исходящих ЛП.
Вероятность нахождения места судна внутри эллипса 0,39, а для выполнения требований ИМО строят эллипс с полуосями, увеличенными в 2,5 раза.
2.5 Аналитическое определение места судна и оценка точности
2.5.1 Определения места судна
Если для определения места судна использовалось более двух навигационных параметров, то в результате мы получим следующую систему уравнений линий положения:
|
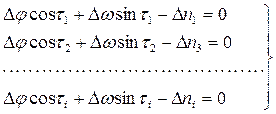
для равноточных измерений. Для неравноточных измерений, нам каждое уравнение необходимо умножить на 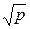 , таким образом мы приведём его к весу равному единице.
, таким образом мы приведём его к весу равному единице.
Проблема состоит в том, что система является неопределённой, так как число уравнений превышает количество неизвестных, а свободные члены D n содержат в себе индивидуальную ошибку измерений. Следовательно, система несовместна, то есть из множества возможных решений не существует такого, которое удовлетворяло бы всем уравнениям системы.
|
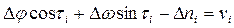
|
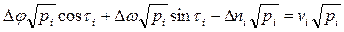
Алгебраически такая система не решаема, можно говорить, только о нахождении таких значений Dj и Dl, которые будут давать минимальные значения квадратов поправки vi, то есть [ vi 2 ]= min. Такой способ решения называется методом наименьших квадратов.
Произведя замены:
ai = cos t i ,
bi = sin t I ,
l =- D n
и решив систему методом наименьших квадратов, мы получим систему двух уравнений, называемых нормальными для равноточных измерений:
|
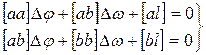
|
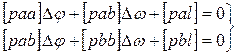
Решив, данную систему методом определителей получим:
|
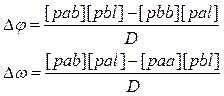
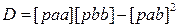
Систему нормальных уравнений можно так же решить методом итераций: в этом случае выделяем неизвестные, после чего система выглядит следующим образом:
|
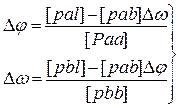
В первом приближении примем Dw = 0:
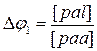 , для Dw 1 учтём, уже найденное Dj 1:
, для Dw 1 учтём, уже найденное Dj 1:
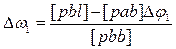 .
.
Второе приближение:
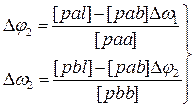
Вычисления продолжают до тех пор, пока разность между двумя последовательными приближениями не окажется в пределах заданной точности e.
Удобство метода - в однообразии расчетов и простоте машинного алгоритма. Полученный таким путем результат ОМС не означает, что обсервованные координаты j 0 и l 0 имеют точность в пределах e, точность j 0 и l 0 оценивается эллипсом или радиальной СКП которых зависит от точности исходных ЛП.
Пример: Расчёт коэффициентов нормальных уравнений.
Дано: Направления градиентов, переносы и СКП 4 линий положения:
| № | t | Dn | mлп |
| 1. | 191,7° | -0,9′ | 0,8 |
| 2. | 56,2° | 0,1 | 1,2 |
| 3. | 31,7° | 1,0 | 1,0 |
| 4. | 79,7° | -0,7′ | 0,5 |
Рассчитать: коэффициенты нормальных уравнений.
| t | a ( cos t ) | b ( sin t ) | l (- D n ) | p | paa | pab | pal | pbb | pbl |
| 191,7° | -0,97 | -0,20 | 0,9′ | 1,6 | 1,50 | 0,31 | -1,45 | 0,06 | -0,30 |
| 56,2° | 0,55 | 0,83 | -0,1 | 0,7 | 0,22 | 0,32 | -0,03 | 0,48 | -0,04 |
| 31,7° | 0,85 | 0,52 | -1,0′ | 1,0 | 0,72 | 0,45 | -0,83 | 0,28 | -0,51 |
| 79,7° | 0,17 | 0,98 | 0,7′ | 4,0 | 0,13 | 0,70 | 0,51 | 3,87 | 2,83 |
|
|
|
| Σ | 2,56 | 1,78 | -1,79 | 4,69 | 1,98 |
2.5.2 Оценка точности места судна
Для расчета эллипса используют уравнения исходных ЛП и их решение методом наименьших квадратов. Поскольку оценка точности места судна выполняется после расчета вероятнейшего места судна как центра эллипса с координатами j 0 и l 0, то итоги вычисления нормальных уравнений легко применить для расчета эллипса погрешностей. При этом учитывается то, что нормальные уравнения являются уравнениями эквивалентных ЛП, т.к. коэффициенты при D j 0 и 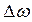 этих уравнений показывают их взаимную перпендикулярность.
этих уравнений показывают их взаимную перпендикулярность.
|
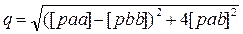
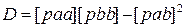
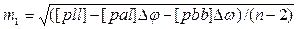
Для n>2
|
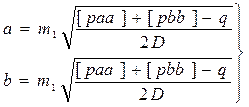
|
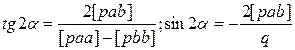
Полуоси можно рассчитать и иным путём:
|
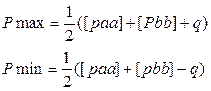
|

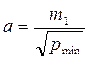 ,
, 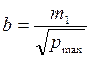
Погрешность по широте и отшествию:
|
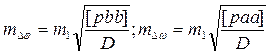
Задания для выполнения индивидуальных заданий раздела 1
Задача №1. Равноточные измерения.
Провести серию из 5-7 измерений навигационным секстаном высоты Солнца, если практические наблюдения невозможны, воспользоваться условием Выполнить следующие задания:
· Привести ОСi к одному зениту и моменту времени.
Рассчитать:
· вероятнейшее значение высоты светила;
· СКП единичного измерения двумя способами;
· предельную погрешность единичного измерения;
· доверительный интервал накрывающий истинное значение СКП единичного значения с надёжностью (вероятностью) 0,90.
· надёжность a определения СКП для доверительного интервала в 0,5 единицу измеряемого параметра (±0,5′)
· СКП вероятнейшего значения;
· предельную погрешность вероятнейшего значения измеренной величины и доверительный интервал, накрывающий истинное значение измеряемой величины с надежностью (вероятностью) 0,95.
· надёжность a для доверительного интервала в одну единицу измеряемого параметра (±1′).
Задача №2. Неравноточные измерения:
Провести серию из 5-7 измерений навигационным пеленга, если практические наблюдения невозможны, воспользоваться условием Задачи №2. Пользуясь методическими указаниями § 2 Главы 1 рассчитать:
· вес каждого измерения.
· вероятнейшее значение измеренного параметра.
· СКП единицы веса.
· СКП вероятнейшего значения и оценить его доверительной оценкой с надёжностью 0.99.
· проверить измерения на промах.
Дата добавления: 2020-04-25; просмотров: 473; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!