Коэффициенты сходства видового состава
Цель работы. Изучить, применяемые методы оценки сходства флор.
Задачи работы:
- Выполнить оценку сходства состава с помощью коэффициента Жаккара.
- Осуществить оценку сходства состава с помощью коэффициента Сёренсена-Чекановского.
Коэффициенты сходства широко применяют в геоботанике [16]. Все коэффициенты сходства прямо или косвенно включают в себя число видов на сравниваемых территориях. При этом площадь участков должна быть одинаковой.
Одним из наиболее часто используемых показателей флористического сходства является коэффициент Жаккара, предложенный им в 1901 г. [16]:
Кж = с/(а+b-c) , (4)
где Кж – коэффициент сходства видового состава участка;
а – число видов на площади 1;
b – число видов на площади 2;
с – число видов, общих для двух участков.
В геоботанике применяют коэффициент Сёренсена-Чекановского (1913 г.):
Кс-ч = 2*с/(а+b) , (5)
Пример. Состав насаждения первого лесного участка 4С2Л2Е2П. Состав насаждения второго лесного участка 5Е3К2Б. Определить коэффициенты сходства видового состава.
Кж = 1/(4+3-1) = 1/6 = 0,17.
Кс-ч = 2*1/(4+3) = 2/7 = 0,29.
Задание. На основе таксационных описаний подобрать участки одного экологического ряда (разнообразие по полноте, бонитету, типу леса, почвенным условиям, крутизне склона, экспозиции склона, возрасту). Общее число участков – 10. Рассчитать степень различия участков по древесному составу на основе формул Жаккара и Сёренсена-Чекановского.
|
|
|
Лабораторная работа
(2 часа)
Основные типы распределений, используемые в лесных экосистемах
Цель работы. Изучить основные типы распределений, используемые при исследовании биологических объектов.
Задачи работы:
- Выполнить предварительную оценку распределения.
- Осуществить аппроксимацию исходного признака стандартной функцией распределения.
Согласно источнику [1] теорию распределений применяют в двух основных направлениях:
-основа статистических выводов (оценка параметров и проверка статистических гипотез);
-средство и метод преставления выборочных распределений.
Практической целью аппроксимации являются: установление закона распределения случайной величины по выборке, а так же аналитическое представление распределения в процессе свёртки информации. Для этого используют следующие операции:
- оценивают способы формирования выборочных совокупностей, проводят визуальный анализ сгруппированных рядов, выполняют анализ статистических показателей;
|
|
|
- по характеристикам ряда распределения устанавливают тип распределения в пределах определённого семейства кривых;
- исходное распределение преобразует в известный «стандартный, простой» тип.
Первая операция включает в себя определение параметров, входящих в заданный закон распределения, вычисление теоретических («выравнивающих») частот по формуле и установление соответствия («согласия») между экспериментальными и теоретическими частотами (по критериям согласия).
Вторая операция применяется при задачах, связанных только со свёрткой информации. В этом случае аналитически представляют большой набор распределений с помощью кривых Пирсона. Недостаток такого подхода применение сложного математического аппарата.
Третья операция используется как для решения аппроксимационных задач, но и для статистического оценивания. В этом случае скошенные и растянутые ряды преобразуют в нормальные и близкие к ним. Выравнивание проводят с помощью семейства кривых Джонсона.
При выборе кривой распределения необходимо руководствоваться следующим:
а) выбирать кривые с минимальным числом параметров;
б) определять параметры через моменты низших порядков (хср.,σ).
|
|
|
Вычисление моментов. Любые статистики являются частным случаем – моментов случайных величин, которые категоризируются на начальные, центральные и основные моменты. При этом моменты описывают форму кривых распределения. Необходимо отметить, что точное описание формы кривой распределения имеет смысл только при значительной численности выборки (n >100) [2].
Начальные моменты mh порядка h получают как среднюю взвешенную величину отклонения от некоторого начального значения x 0, возведённого в степень h:
mh = 
, (6).
Центральные моменты (μ h), получают на основе предыдущей формулы (1) путём замены отклонений значений случайных величин от произвольного x0 отклонениями от среднего значения x ср:
μh = 
, (7).
Наибольшее значение имеют основные моменты (безразличные величины) на основе соотношения которых и определяют форму кривых распределений:
|
|
|
rh = 
, (8).
Форму кривых определяют по основным моментам 3-го и 4-го порядка.
r3=β1= 
= 
, (9).
r4=β2= 
= 
, (10).
Пример расчёта центральных и основных моментов методом отклонений приведённых в таблице 1.
Таблица 1 - Расчёт центральных и основных моментов методом отклонений (пихта – Бирюсинское лесничество учебно-опытного лесхоза)
| Середина класса, Хi | Число стволов, ni | Центральные отклонения | |||
| Xi-Xср | (Xi-Xср)2 | (Xi-Xср)3 | (Xi-Xср)4 | ||
| 4 | 27 | ||||
| 8 | 38 | ||||
| 12 | 30 | ||||
| 16 | 16 | ||||
| 20 | 19 | ||||
| 24 | 21 | ||||
| 28 | 17 | ||||
| 32 | 13 | ||||
| 36 | 3 | ||||
| 40 | 1 | ||||
| Хср=18,3 см | Σ | Σ | Σ | Σ | Σ |
Задание. Построить ряд распределения по диаметру деревьев пихты, выполнить визуальную предварительную оценку распределения, построить полигон и куммуляту вариационного ряда, вычислить центральные и основные моменты по соотношению β1 и β2, определить форму кривой распределения (равномерное, U, Ј, β - образное распределение, нормальное, γ - гамма распределение, логнормальное и показательное распределение).
Лабораторная работа
(2 часа)
Анализ распределения
Цель работы. Научиться анализировать признак на соответствие «нормальному» распределению.
Задачи работы:
- Выполнить оценку формы распределения.
- Осуществить предварительный анализ распределения биологического признака.
Идеальным распределением с точки зрения оценок, сравнения и т.д. является «нормальная кривая». Подробно данная функция изучалась в курсе «Математические методы в расчётах на ЭВМ». Рассмотрим терминологические аспекты в особенностях формы распределения [2].
Если кривая близка к нормальной, то обычно это означает, что варьирование изучаемого явления обусловлено множеством мелких случайных причин. Резкие отклонения кривой распределения от нормальной и особенно появление многовершинности (полимодальные кривые) предполагают, либо наличие сильного специфического фактора, действующего на явление, либо гетерогенность материала [2] (рисунок 1).
По величине асимметрии и эксцесса можно судить о форме кривой и общих тенденциях.
А = 
, (11)
Е = 
- 3 , (12)
| равномерное |
| полимодальное |
| нормальное |
| эксцессивное |
| U - образное |
| депрессивное |
Рисунок 1 – Стандартные кривые распределения случайных величин
где А- асимметрия;
Е- эксцесс;
σ - стандартное отклонение;
хi - случайная величина (варианта);
xср- средняя величина;
n- объём выборки.
Анализ распределения [2,3] (рисунок 1).
А=Е=0 – нормальное распределение.
А<0 – левая симметрия.
А >0 – правая симметрия.
Е>0- эксцессивное распределение.
Е<0 – депрессивное распределение.
±А<0,5 – малое смешение (симметричное, правостороннее или левостороннее распределение).
0,5>±А<1,0- среднее смешение (асимметричное, правостороннее или левостороннее распределение).
±А>1,0- большое смешение (крайне асимметричное, правостороннее или левостороннее распределение).
0<Е< 0,5 – незначительная эксцесcивность (симметричное распределение).
Е>0,5 – эксцессивное распределение.
0>Е <- 0,5 – незначительная депрессивность (симметричное распределение).
-0,5 >Е<-2 – депрессивное распределение.
Е >-2 – полимодальное распределение (разделение на 2 части).
Задание. Рассчитать значение асимметрии и эксцесса. Выполнить предварительный анализ формы распределения. Провести описание строения выборки с биологической интерпретации.
Лабораторная работа
(2 часа)
Нормальное распределение
Цель работы. Изучить особенности «нормального» распределения
Задачи работы:
- Построить график эмпирического распределения.
- Рассчитать теоретические частоты, соответствующие нормальному распределению.
Закон нормального распределения играет особую роль, как в теории статистического анализа, так и в его приложениях [1]. Центральная придельная теорема (А.Ляпунов, 1901) утверждает, что распределение суммы независимых случайных величин (u=1,2, … , n) стремится к нормальному при неограниченном увеличении n, если все величины имеют конечные средние дисперсии и не одна из них по своему значению резко не отличается от других [1].
Г.Н.Зайцев [4] указывает на следующее соответствие нормальному распределению: симметричная, колоколообразная, двускатная кривая распределения; соотношение средней арифметической и сигмы М = 3 *σ или V= 33 %.
Ю.Г. Пузаченко [5] отмечал, что нормальное распределение отражает равновесное состояние системы, когда варьирование её состояний или положения её элементов определяются только тепловым «шумом». В соответствии с этим его энтропия относительно всех других непрерывных распределений максимальна и прямо связана с дисперсией.
Нормальное распределение описывается следующей функцией:
f (x) = 
, (13)
Проверка на соответствие исходного вариационного ряда нормальному распределению позволяет в полной мере применить статистический аппарат (обосновано) для интерпретации биологических выводов.
Для этого сопоставляют эмпирические частоты теоретическому распределению (производят выравнивание распределения).
Для нахождения числа вариант (ni) в пределах каждого интервала кривой нормального распределения (по закону Гаусcа - Лапласа) пользуются следующей рабочей формулой:
ni, = 
, (14)
где ni, - теоретическая частота;
n- объём выборки, штук;
σ- стандартное отклонение;
di- классовый интервал;
f(xi) - значение функции нормального распределения для случайной величины xi;
Применение нормированного отклонения t = 
позволяет в значительной степени упростить вычисления и устранить влияние конкретного признака на распределение:
f (t) = 
, (15)
В окончательном виде:
n = 
, (16)
где t- случайная величина, для которой математическое ожидание равно 0, а среднеквадратическое отклонение равно 1.
Расчёт теоретических частот нормального распределения для эмпирического ряда распределения деревьев по диаметру приведены в таблице 2 [3].
Относительно ординаты нормального распределения (h) определяют по Приложению Б.
Наибольшая ордината (H) рассчитывается по формуле:
Н =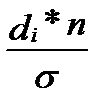 
, (17)
Таблица 2- Вычисление частот нормального распределения деревьев пихты по диаметру на высоте груди способом наибольшей ординаты
Xср = 28,0 см σ = 6,27 см
| Хi , см | ni , шт | α=хi-xср, центральное отклонение | t = 
нормированное
отклонение
| h, относительная ордината | h*H, фактическая ордината | ni, , округленная частота |
| 12 | 1 | -16 | -2,55 | 0,0154 | 0,98 | 1 |
| 16 | 5 | -12 | -1,91 | 0,0644 | 4,11 | 4 |
| 20 | 12 | -8 | -1,28 | 0,1758 | 11,22 | 11 |
| 24 | 17 | -4 | -1,064 | 0,3251 | 20,74 | 21 |
| 28 | 28 | 0 | 0,00 | 0,3989 | 25,45 | 26 |
| 32 | 20 | 4 | 0,64 | 0,3251 | 20,74 | 21 |
| 36 | 12 | 8 | 1,28 | 0,1758 | 11,22 | 11 |
| 40 | 4 | 12 | 1,91 | 0,0644 | 4,11 | 4 |
| 44 | 1 | 16 | 2,55 | 0,0154 | 0,98 | 1 |
| Σ | 100 | 0 | 99,55 | 100 |
Задание. Построить график эмпирического распределения. Рассчитать теоретические частоты, соответствующие нормальному распределению. Построить и сопоставить теоретическое и эмпирическое распределение. Определить вероятность встретить в данной совокупности деревья с диаметром d = 18 см, d = 37 см.
Лабораторная работа
(2 часа)
Распределение Максвелла
Цель работы. Изучить особенности распределения Максвелла.
Задачи работы:
- Построить график эмпирического распределения.
- Рассчитать теоретические частоты, соответствующие распределению Максвелла.
- Сопоставить эмпирическое и теоретическое распределение Максвелла.
Кривая распределения эмпирических частот вариационного ряда положительных чисел, обладающего умеренной асимметрией, может быть аппроксимирована распределением Максвелла [4]. Кривая частот рассматриваемого типа распределения удобна тем, что строится по средствам уравнения, определяемого всего одним параметром. Она достаточно гибка и может быть применена для выравнивания асимметричных распределений различных биологических признаков, величины которых изменяются по непрерывному типу.
Теоретическая частота распределения Максвелла определяется по следующей формуле:
n, =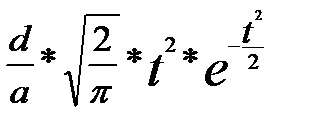 
, (18)
где t = 
- нормированное отклонение.
Порядок расчёта [4] частот распределения Максвелла на примере распределения периодов продолжительности цветения в днях 381 вида деревьев и кустарников.
При этом период цветения – существенно положительная величина и не может принимать отрицательных значений; ряд- умеренно асимметричен.
1. Вычисляем среднюю арифметическую величину хср = 16, среднее квадратическое отклонение σ = 12,4 .
2. Коэффициент вариации (V) распределения Максвелла является величиной постоянной:
V = 
= 0,422 или 42,2 %.
В нашем случае V = 
= 
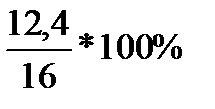= 75 %.
3. Получаем параметр распределения
a = 
=> a = 
= 10,254.
4. Вычисляем среднее квадратическое отклонение распределения Максвелла:
σ = a* 
=> 10,254*0,67345 = 6,905
σ2 = 47,683
5. Мода
M0 = a* 
=> 10,254*1,41421 = 14,501
6. Медиана
Ме = 1,538*а => 1,538*10,254 = 15,771
Для случаев асимметричных распределений, мода и особенно медиана адекватнее характеризуют ряд, чем средняя арифметическая величина.
7. Вычисляем величину наибольшей ординаты:
H = 
=> 
8. Заполняем таблицу 3
Таблица 3 - Вычисление частот распределения Максвелла
| Период цветения, день, Хi | Число видов (ni), шт | 
| 
| t2* 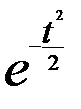 (f,)
| f0 =f,*H | n, =f0*n |
| 5 | 37 | 0,23777 | 0,88798 | 0,211 | 0,164 | 62,6=63 |
| 15 | 238 | 2,1401 | 0,34298 | 0,734 | 0,571 | 217,6=218 |
| 25 | 78 | 5,9443 | 0,051196 | 0,304 | 0,237 | 90,2=90 |
| 35 | 9 | 11,651 | 2,951*10-3 | 3,439*10-2 | 0,027 | 10,2=10 |
| 45 | 8 | 19,259 | 6,576*10-5 | 1,267*10-3 | 9,86*10-4 | 0,4=0 |
| 55 | 3 | 28,77 | 55,659*10-7 | 1,628*10-5 | 1,27*10-5 | 4,8*10-3=0 |
| 65 | 3 | 40,183 | 1,880*10-9 | 7,556*10-8 | 5,88*10-8 | 2,2*10-5=0 |
| 75 | 1 | 53,498 | 0 | 0 | 0 | 0 |
| 85 | 2 | 68,716 | 0 | 0 | 0 | 0 |
| 95 | 0 | 85,835 | 0 | 0 | 0 | 0 |
| 105 | 1 | 104,86 | 0 | 0 | 0 | 0 |
| 115 | 1 | 125,78 | 0 | 0 | 0 | 0 |
| Σ | 381 | 381 |
Биологический вывод. Варьирование периода цветения у видов деревьев и кустарников очень велико. Величина нормы для периода цветения этих видов должна находиться в пределах хср ± σ = 16 ± 12,4 ,т.е. от 4 до 29 дней. В этот период укладывается цветение 362 видов из 381, т.е. позволяющее большинство. Остальные 19 видов являются ремонтантными или вторично цветущими.
Задание. Построить график распределения исходного ряда. Вычислить теоретические частоты распределения Максвелла. Построить и сопоставить эмпирическое и теоретическое распределение Максвелла.
Лабораторная работа
(2 часа)
Распределение Рэлея
Цель работы. Изучить особенности распределения Рэлея.
Задачи работы:
- Построить график эмпирического распределения.
- Рассчитать теоретические частоты, соответствующие распределению Рэлея.
- Сопоставить эмпирическое и теоретическое распределение Рэлея.
К числу типов распределений, определяемых одним параметром, относится так же распределение Рэлея, которое пригодно для аппроксимации умеренно асимметричных вариационных рядов, составленных из значений принимающих только положительные значения. Критерием применения данного распределения служит следующее соотношение: σ = 0,52*хср т.е. среднее квадратическое отклонение должно быть примерно в 2 раза меньше средней арифметической величины [4] . В качестве примера рассмотрим распределение числа побегов у 205 сортов пиона. При следующих статистических характеристиках выборки хср = 22; σ = 11,78; А = 0,604; Е = -0,084.
Порядок расчёта следующий.
1. Основной параметр определяется по формуле:
а2 = 
= 
= 310,24
2. Мода
М0 = а = 
= 17,61
3. Дисперсия
σ2 = а2 * (2- 
) = 310,24*(2- 
) = 133,16
4. Среднее квадратическое отклонение
σ = 
= 
= 11,54
5. Медиана
Ме = 
= 
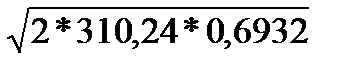= 20,74
Функция вычисления теоретических частот Рэлея имеет следующий вид:
n,= 
* 
*n*di, (19)
Расчет теоретических частот приведен в таблице 4.
Таблица 4 – Частоты распределения Рэлея
| Число побегов, хi | Число пионов, ni | 
| *
| f,0 = f*di | n,= f*di*n |
| 5 | 21 | 0.0161 | 0.0155 | 0.1084 | 22.2=22 |
| 12 | 48 | 0.0387 | 0.0307 | 0.2147 | 44.0=44 |
| 19 | 50 | 0.0612 | 0.0342 | 0.2396 | 49.1=49 |
| 26 | 29 | 0.0838 | 0.0282 | 0.1973 | 40.45=41 |
| 33 | 34 | 0.1064 | 0.0184 | 0.1287 | 26.4=26 |
| 40 | 13 | 0.1289 | 0.0098 | 0.0685 | 14.0=14 |
| 47 | 7 | 0.1515 | 0.0043 | 0.0302 | 6.2=6 |
| 54 | 2 | 0.1741 | 0.0016 | 0.0111 | 2.3=2 |
| 61 | 1 | 0.1966 | 4.8*10-4 | 0.0034 | 0.7=1 |
| 205 | 1.0018 | 205 |
Задание. Построить график распределения исходного ряда. Вычислить теоретические частоты распределения Рэлея. Построить и сопоставить эмпирическое и теоретическое распределение Рэлея.
Лабораторная работа
(2 часа)
Показательное распределение
Цель работы. Изучить особенности показательного распределения.
Задачи работы:
- Построить график эмпирического распределения.
- Рассчитать теоретические частоты, соответствующие показательному распределению.
- Сопоставить эмпирическое и теоретическое показательное распределение.
По этому типу распределения выравнивают эмпирический ряд, частоты которого представлены с резко выраженной правосторонней (или положительной) асимметрией, а средняя арифметическая величина соответствует по своему значению стандартному отклонению: xср≈σ. Второе условие – варианты должны быть положительными числами, или равными нулю [4]. Параметром показательной функции является число положительное, обратное средней арифметической величине:
а = 
.
Дисперсия: σ2 = 
.
Медиана: Ме = 0,693*Хср
Стандартное отклонение: σ = 
Коэффициент вариации: V = 
как один из признаков показательного распределения. Второй критерий - это величина моды М0 = 0.
Теоретическая частота показательного распределения:
n, = n*(e-a*xвi-1 – e-a*xвi), (20)
где a - параметр показательной функции;
xвi-1 - верхняя граница предыдущего класса распределения вариант;
xвi - верхняя граница последующего класса распределения вариант;
n – объем выборки, шт.
Пример. Распределение 2619 побегов в зависимости от числа соцветий однолетнего растения гелениума осеннего.
Статистики ряда имеют следующие показатели: А=1,456; Е=2,340; V=83,4%; Хср=44,83; σ=37,38; Р=1,36%.
Расчет теоретических частот показательного распределения представлен в таблице 5.
Таблица 5 – Теоретические частоты показательного распределения
| Границы классов | Хi | ni, шт | Верхняя раница, Хв | а* Хв | е-а* Хв | е-а* Хвi-1* *e-а* Хвi | n, |
| 0 | 0 | 1 | - | - | |||
| 0-29 | 15 | 1249 | 30 | 0,6692 | 0,5121 | 0,4879 | 1278 |
| 30-59 | 45 | 639 | 60 | 1,3384 | 0,2623 | 0,2498 | 654 |
| 60-89 | 75 | 419 | 90 | 2,0076 | 0,1343 | 0,1280 | 335 |
| 90-119 | 105 | 185 | 120 | 2,6768 | 0,0688 | 0,0655 | 172 |
| 120-149 | 135 | 89 | 150 | 3,3461 | 0,0352 | 0,0336 | 88 |
| 150-179 | 165 | 20 | 180 | 4,0153 | 0,0180 | 0,0172 | 45 |
| 180-209 | 195 | 10 | 210 | 4,6845 | 0,0092 | 0,0088 | 23 |
| 210-239 | 225 | 8 | 240 | 5,3537 | 0,0047 | 0,0045 | 12 |
| 240-269 | 255 | 0 | 270 | - | - | 0,0023 | 6 |
| Σ | 0,998 | 2613 |
Задание. Построить графики распределения исходного ряда. Вычислить теоретические частоты показательного распределения. Построить и сопоставить эмпирическое и теоретическое показательное распределение.
Лабораторная работа
(2 часа)
Дата добавления: 2020-04-25; просмотров: 1246; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!