Приведение к каноническому виду уравнений гиперболического типа

Поскольку для уравнений гиперболического типа , то уравнения (5.2 а) и (5.2 б) различны.

 

 

Тогда (см. выражения после уравнения (4.2)):

, , .

         

Делим (4.2) на , получаем канонический вид уравнения гиперболического типа:

 

.

 

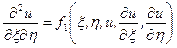Проверим, что наша замена невырожденная, то есть .

Рассмотрим  - общий интеграл уравнения (5.2 а).

Дифференцируем его:

 

,

 

.

 

Рассмотрим 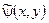 - общий интеграл уравнения (5.2 б).

Дифференцируем его:

 

,

 

.

 

В результате имеем:

 

;   .

 

Стало быть, замена невырожденная.

 

 

Лекция 2 ПРИВЕДЕНИЕ К КАНОНИЧЕСКОМУ ВИДУ УРАВНЕНИЙ

ПАРАБОЛИЧЕСКОГО И ЭЛЛИПТИЧЕСКОГО ТИПОВ

 

Поскольку для уравнений параболического типа , то уравнения (5.2 а) и (5.2 б) одинаковые и имеют вид:

 

.

 

Пусть  - общий интеграл этого уравнения.

 

 

Можно доказать, что в качестве функции  допустимо брать либо x, либо y.

Тогда (см. выражения после уравнения (4.2)):

 

, , .

 

Докажем от противного, что 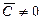. Учтём, что , а значит и

 

.

 

При этом конечно .

Пусть (с учётом определения )

=

 

= = .

 

Откуда:

 

,

 

. (*)

 

Учтём теперь, что  - общий интеграл уравнения (5.2 а), которое теперь имеет вид:

 

,

 

.

 

Тогда:

 

. (**)

 

Сравнивая (*) и (**), находим:

 

,

 

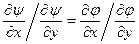 то есть получили противоречие . Следовательно .

Делим (4.2) на 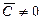, получаем канонический вид уравнения параболического типа:

 

.

 

Поскольку для уравнений эллиптического типа , то (5.2 а) и (5.2 б) соответственно имеют вид:

 

,   .

 

Запишем  - и  - общие интегралы уравнений (5.2 а) и (5.2 б):

 

,

 

,

 

и сделаем в (2.1) замену переменных:

 

 

Так как , то , .

Делим (4.2) на . Получаем канонический вид уравнения эллиптического типа в комплексной области 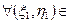С²:

 

,

 

,

 

.

 

Пересчитаем смешанную производную в действительных переменных  и :

 

; .

 

В итоге получаем канонический вид уравнения эллиптического типа в действительной области R²:

 

.

 

 

Практические занятия

Рассмотрим примеры решения задач по теме лекций

Пример 1. Привести уравнение

 

 

к каноническому виду.

Решение:

В данном случае

, , .

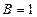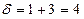, - гиперболический тип.

Составим уравнения характеристик:

 

,

 

,

 

,

 

, ,

 

, ,

, , , ;

 

  ;

 

  ;

 

=

 

= ;

 

=

 

= ;

 

 

.

 

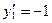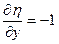Подставив найденные выражения в исходное дифференциальное уравнение, получаем:

 

 

,

 

,

 

.

       

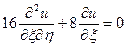Пример 2. Привести уравнение

 

 

к каноническому виду.

Решение:

В данном случае

, , .

 - параболический тип.

Составим уравнения характеристик:

 

,

 

,

 

 

, .

 

Сделаем замену переменных: , 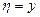(произвольнаяфункция).

 

, , , ;

 

; ;

 

= ; = ; .

 

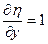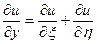Подставив найденные выражения в исходное дифференциальное уравнение, получаем:

 

,

 

.

 

Пример 3. Привести уравнение

 

 

к каноническому виду.

Решение:

В данном случае

А= xy ², В= - x² y, С=x³.

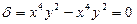,  - параболический тип.

Составим уравнения характеристик:

 

, ,

 

,

 

,

 

 

,

 

.

 

Сделаем замену переменных: , (произвольная функция).

 

, , , ; , ,

 

,

 

= ,

 

= ,

 

= .

 

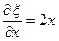Подставив найденные выражения в исходное дифференциальное уравнение, получаем:

 

 

,

 

,

 

.

 

Пример 4. Привести уравнение

 

к каноническому виду.

Решение:

В данном случае

   , , .

,  - эллиптический тип.

 Составим уравнения характеристик:

 

,

 

,

 

.

 

Сделаем замену переменных: , .

 

, , , ,

 

, .

 

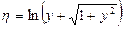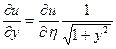Подставив найденные выражения в исходное дифференциальное уравнение, получаем:

 

.

 

 

---

Дата добавления: 2020-04-25; просмотров: 186; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!