Прогнозирование по временным рядам
Расчетная работа № 2
Прогнозирование выходных переменных
Прогнозирование выходных переменных с использованием многопараметрической математической модели
Цель
Освоить метод прогнозирования по математической модели.
Теоретические аспекты
Прогнозирование выходной величины объекта необходимо рассматривать в рамках вероятностных категорий.
Можно использовать линейную регрессионную модель
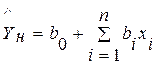 , (2.1)
, (2.1)
где н = 1,2,…. ;
bi - оценки коэффициентов управления регрессии (адекватного по критерию Фишера[8]);
XiH - значимо влияющие на y выходные переменные в момент времени Н;
Ŷн - прогнозируемое условное среднее значение выходной величины в момент времени Н.
Величина ошибки прогнозирования зависит от наличия помех, качества аппроксимации объекта математической моделью, точности учета динамики процесса, дрейфа характеристик объекта, величины времени экстраполяции и др.
Единичное предсказание выходной величины по уравнению (2.1) с доверительной вероятностью P = 0,95 находится в интервале шириной
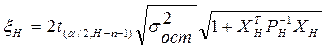 , (2.2)
, (2.2)
где t(α/2,H-n-1) - табличное значение t – критерия с Н – n – 1 степенями свободы, α = 1 – P;
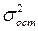 - оценка остаточной дисперсии по уравнению (2.1);
- оценка остаточной дисперсии по уравнению (2.1);
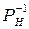 - оценка матрицы
- оценка матрицы 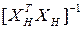 .
.
Тогда для уравнения значимости α имеем
|
|
|
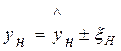 ˙ (2.3)
˙ (2.3)
Точечная ошибка прогноза определяется
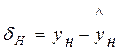 .
.
Оценка качества прогноза на интервале времени определяется в виде дисперсии
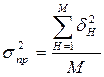 , (2.4)
, (2.4)
и среднеквадратической ошибки
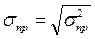 .
.
Задание
На основе исходных данных ретроспективной информации (см. таблицу 2.7) получить многопараметрическую математическую модель. Используя ее, выполнить прогноз выходных параметров при наличии векторов входных параметров. Проанализировать полученные данные и сделать вывод.
Исходные данные
Номер варианта соответствует двум последним цифрам зачетной книжки. Если число больше 30, то из него следует вычесть 30 (возможно, не один раз), чтобы получилось число в диапазоне от 1 до 30 включительно. Каждому варианту соответствует 4 переменные исходных совокупностей из таблицы 2.8.
Указания к выполнению
1 Разделить исходные данные на выборку ретроспективной информации объемом N=10 и выборку, необходимую для прогнозирования (N=5).
2 Построить по программе Kralis2003 многопараметрическую регрессионную математическую модель по первым десяти значениям выборочной совокупности (см. таблицу 2.7).
|
|
|
3 По полученной математической модели сделать прогноз значений выходной величины на оставшихся пяти векторах выборочной совокупности входных параметров.
4 Сравнить полученные прогнозируемые значения выходной величины с реальными экспериментальными данными. Вычислить дисперсию, среднеквадратическое отклонение ошибки прогноза.
5 На основе полученных данных сделать вывод о качестве прогноза.
Пример выполнения
Исходные данные:
Таблица 2.1 – Исходные данные
| № | Y3 | X3 | X4 | X6 | |
| 1 | 27,0 | 32,3 | 61,7 | 3,5 | Данные для построения математической модели |
| 2 | 25,8 | 31,0 | 63,5 | 3,0 | |
| 3 | 27,8 | 33,2 | 59,5 | 2,1 | |
| 4 | 27,0 | 32,0 | 63,0 | 2,7 | |
| 5 | 29,0 | 35,0 | 58,0 | 1,7 | |
| 6 | 27,6 | 32,6 | 61,5 | 2,5 | |
| 7 | 28,4 | 34,0 | 60,0 | 2,0 | |
| 8 | 31,2 | 35,8 | 64,5 | 1,1 | |
| 9 | 28,5 | 34,2 | 59,7 | 2,0 | |
| 10 | 30,3 | 36,5 | 55,2 | 1,5 | |
| 11 | 31,9 | 38,0 | 53,7 | 0,8 | Данные для получения прогноза |
| 12 | 30,5 | 35,7 | 52,6 | 0,5 | |
| 13 | 32,5 | 39,1 | 55,6 | 1,2 | |
| 14 | 31,5 | 36,3 | 55,0 | 0,3 | |
| 15 | 31,6 | 37,2 | 52,5 | 0,7 |
|
|
|
Запустите программу Kralis2003. Выберите «Работа 4», укажите номер варианта (например, 8) и нажмите «ввод». Вновь нажмите «Работа 4», но теперь укажите возможность ввода данных с клавиатуры с установкой «Объем выборочной совокупности», равной 10 и «количество векторов данных», равной 4. После этого нажмите кнопку «Выполнить». В результате получена следующая математическая модель:
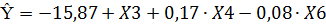
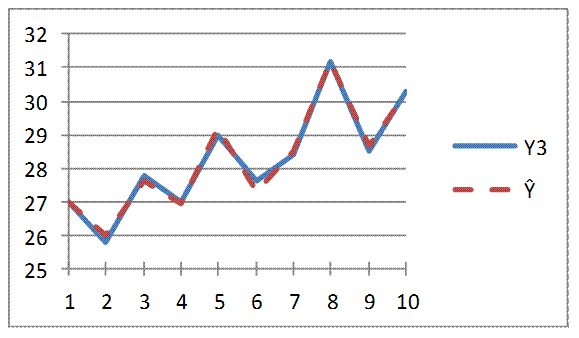
Рисунок 2.1 – Исходные значений и значений по модели
Поочередно подставим в математическую модель 5 значений переменных Х3, Х4, Х6 из выборки, необходимой для прогнозирования, и вычислим прогнозируемые значения выходной величины.
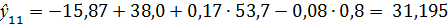
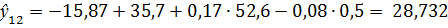
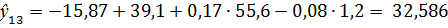
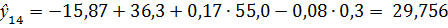
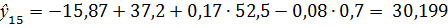
Сравним полученные значения с исходными:
Таблица 2.2 – Сравнение исходных и прогнозируемых данных
| № | Y3 | Ŷ |
| 1 | 27,0 | 26,97 |
| 2 | 25,8 | 26,02 |
| 3 | 27,8 | 27,61 |
| 4 | 27,0 | 26,96 |
| 5 | 29,0 | 29,19 |
| 6 | 27,6 | 27,32 |
| 7 | 28,4 | 28,5 |
| 8 | 31,2 | 31,16 |
| 9 | 28,5 | 28,65 |
| 10 | 30,3 | 30,23 |
| 11 | 31,9 | 31,195 |
| 12 | 30,5 | 28,732 |
| 13 | 32,5 | 32,586 |
| 14 | 31,5 | 29,756 |
| 15 | 31,6 | 30,199 |
Рис. 2.2 – Сравнение исходных и прогнозируемых данных
|
|
|
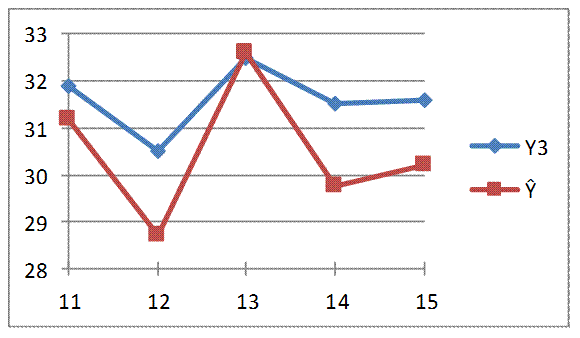
Найдем ошибку прогноза:
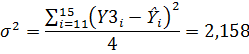
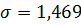
Вывод:
На основании вычислений, выполненных в программе Kralis2003, имеем:
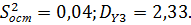
Тогда:
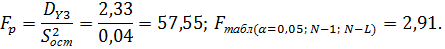
Так как 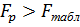 , то различие между дисперсией
, то различие между дисперсией 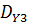 и остаточной дисперсией
и остаточной дисперсией 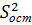 с доверительной вероятностью 0,95 статистически значимо, следовательно полученная математическая модель адекватна.
с доверительной вероятностью 0,95 статистически значимо, следовательно полученная математическая модель адекватна.
Многопараметрическая математическая модель позволяет делать качественный прогноз выходной величины и может быть использована при прогнозировании и управлении процессами с транспортными запаздываниями в каналах управления.
Содержание отчета
1. Формулировка задания
2. Исходные данные
3. Расчетно-графическая часть
4. Вывод
Прогнозирование по временным рядам
Цель
Исследование сигналов с помощью временных рядов. Прогнозирование случайных величин.
Задание
Произвести прогноз случайной последовательности, используя временные ряды.
Указания к выполнению
1 Построить временной ряд на основе исходных данных (см таблицу 2.7 по варианту, определенному в пункте 2.2.1.4).
2 Выявить линейный тренд временного ряда 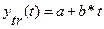 , используя метод наименьших квадратов.
, используя метод наименьших квадратов.
3 Получить центрированную функцию прогнозируемой величины относительно тренда 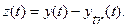
4 Для построения математической модели, описывающей данный временной ряд необходимо определить порядок модели (рекомендуется не более 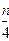 ) и оценку значений ее коэффициентов.
) и оценку значений ее коэффициентов.
5 Вычислить коэффициенты автокорреляции 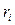 с 1 по n порядок по формуле (2.6), где n – порядок модели.
с 1 по n порядок по формуле (2.6), где n – порядок модели.
6 Получить прогнозирующую модель 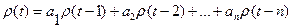 , где коэффициенты аi определяются выражением (2.5), n - размерность модели.
, где коэффициенты аi определяются выражением (2.5), n - размерность модели.
7 Последовательно подставляя 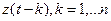 в прогнозирующую модель произвести прогноз значений временного ряда на один, два и три такта времени вперед. Изобразить прогноз графически.
в прогнозирующую модель произвести прогноз значений временного ряда на один, два и три такта времени вперед. Изобразить прогноз графически.
8 Вычислить ошибки прогноза (D, δ, ε).
9 На основе полученных данных сделать вывод о качестве прогноза.
Используемые формулы:
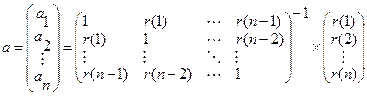 , (2.5)
, (2.5)
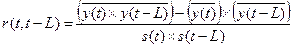 , (2.6)
, (2.6)
где 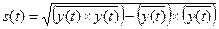 ,
,
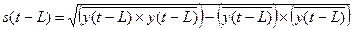 ,
,
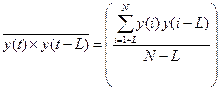 ,
, 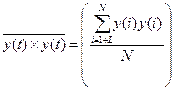 ,
, 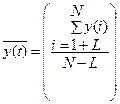 ,
,
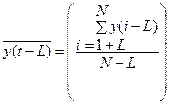
Здесь 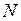 - длина ряда. График зависимости значений коэффициентов автокорреляции от величины лага L называется коррелограммой.
- длина ряда. График зависимости значений коэффициентов автокорреляции от величины лага L называется коррелограммой.
Cдвиг по времени L называется лагом, который определяет порядок коэффициента автокорреляции. Если L = 1, то имеем коэффициент автокорреляции 1-го порядка 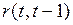 если L = 2, то коэффициент автокорреляции 2-го порядка
если L = 2, то коэффициент автокорреляции 2-го порядка 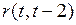 и т.д.
и т.д.
Отметим два важных свойства коэффициента автокорреляции:
1) Он характеризует тесноту линейной связи текущего и предыдущего уровней. Поэтому по коэффициенту автокорреляции можно судить о наличии только линейной тенденции.
2) По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Многие временные ряды экономических данных содержат положительную автокорреляцию уровней, однако при этом могут иметь убывающую тенденцию.
Модель 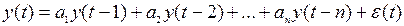 , (2.7) называется моделью авторегрессионного процесса и обозначается
, (2.7) называется моделью авторегрессионного процесса и обозначается 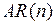 , где n – максимальный учитываемый лаг.
, где n – максимальный учитываемый лаг.
Построение модели AR ( n ) типа (2.7), адекватной реальному временному ряду 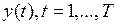 , предполагает решение двух взаимосвязанных задач: определение порядка модели n и оценка значений ее коэффициентов.
, предполагает решение двух взаимосвязанных задач: определение порядка модели n и оценка значений ее коэффициентов.
При определении порядка модели необходимо учитывать, что с увеличением лага на единицу число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается на 1. Поэтому обычно максимальный порядок коэффициента автокорреляции равен N/4, где 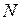 - длина анализируемого ряда.
- длина анализируемого ряда.
Лаг L, при котором автокорреляция 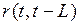 максимальна, определяет структуру временного ряда. Если максимум соответствует L = 1, то исследуемый ряд содержит только тенденцию. Если L>1, то ряд содержит (помимо тенденции) колебания периодом L. Если ни один из
максимальна, определяет структуру временного ряда. Если максимум соответствует L = 1, то исследуемый ряд содержит только тенденцию. Если L>1, то ряд содержит (помимо тенденции) колебания периодом L. Если ни один из 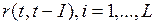 не является значимым, можно сделать одно из предположений:
не является значимым, можно сделать одно из предположений:
- временной ряд не содержит тенденций и циклических колебаний, а его уровень определяется случайной компонентой;
- временной ряд содержит нелинейную тенденцию, для выявления которой необходимы дополнительный анализ.
Без ограничения общности в дальнейшем будем предполагать, что математическое ожидание ряда 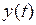 равно нулю (
равно нулю ( 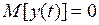 ). Если это не так, то вместо переменной
). Если это не так, то вместо переменной 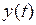 в выражении (2.7) можно рассмотреть центрированную переменную
в выражении (2.7) можно рассмотреть центрированную переменную 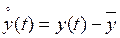 , где
, где 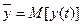 , при этом
, при этом 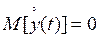 . Если временной ряд имеет тренд, то из значений ряда необходимо вычесть трендовую составляющую.
. Если временной ряд имеет тренд, то из значений ряда необходимо вычесть трендовую составляющую.
Из выражения (2.5) следует, что параметры модели ai , 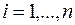 могут быть выражены через коэффициенты автокорреляции:
могут быть выражены через коэффициенты автокорреляции:
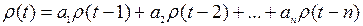 , (2.8)
, (2.8)
которое связывает коэффициенты автокорреляции процесса 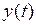 и коэффициенты модели AR ( n ). Подставив в (2.8) вместо значений коэффициентов автокорреляции
и коэффициенты модели AR ( n ). Подставив в (2.8) вместо значений коэффициентов автокорреляции 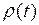 процесса
процесса 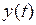 их выборочные оценки
их выборочные оценки 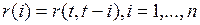 , получим следующую систему линейных уравнений
, получим следующую систему линейных уравнений
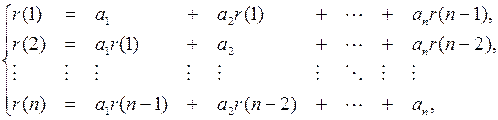 (2.9)
(2.9)
в которой известными являются оценки коэффициентов автокорреляции 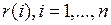 , а неизвестными – оценки коэффициентов модели AR ( n )
, а неизвестными – оценки коэффициентов модели AR ( n ) 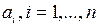 .
.
Поясним, как систему (2.9) можно получить из (2.7). Умножим обе части (2.7) на 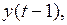 вычислим математическое ожидание и результат разделим на
вычислим математическое ожидание и результат разделим на 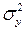 (предполагается, что ряд стационарный). В результате получим первое уравнение системы (2.9). Повторив описанную операцию с
(предполагается, что ряд стационарный). В результате получим первое уравнение системы (2.9). Повторив описанную операцию с 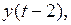 получим второе уравнение системы, и так далее.
получим второе уравнение системы, и так далее.
Систему (2.9) называют уравнениями Юла-Уокера, а полученные на их основе значения 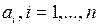 - оценками коэффициентов модели авторегрессии AR ( n ) Юла-Уокера. Решение уравнения (2.9) можно представить в матричной форме (2.5).
- оценками коэффициентов модели авторегрессии AR ( n ) Юла-Уокера. Решение уравнения (2.9) можно представить в матричной форме (2.5).
Пример выполнения
В качестве входных данных будем использовать первые 12 данных Y3 из таблицы 2.3 и по ним проведем прогноз 3-х оставшихся значений.
Таблица 2.3 – Исходные данные
| № | Y3 | |
| 1 | 27,0 | Данные для построения математической модели |
| 2 | 25,8 | |
| 3 | 27,8 | |
| 4 | 27,0 | |
| 5 | 29,0 | |
| 6 | 27,6 | |
| 7 | 28,4 | |
| 8 | 31,2 | |
| 9 | 28,5 | |
| 10 | 30,3 | |
| 11 | 31,9 | |
| 12 | 30,5 | |
| 13 | 32,5 | Данные для прогнозирования |
| 14 | 31,5 | |
| 15 | 31,6 |
1. Построим исходный временной ряд
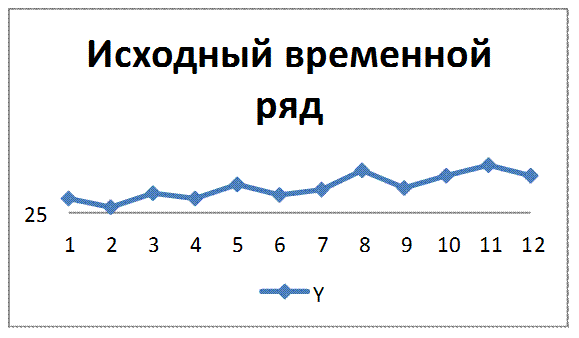
Рис 2.3 – Исходный временной ряд
2. С помощью метода наименьших квадратов найдем коэффициенты модели, описывающей тренд временного ряда
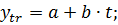 (2.10)
(2.10)
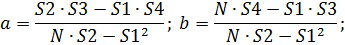
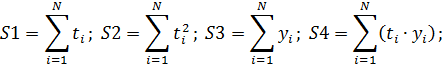
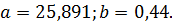
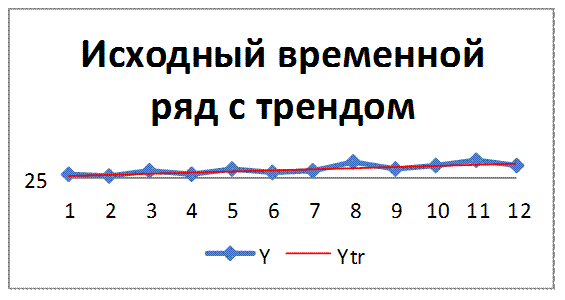 |
Рис. 2.4 – Исходный временной ряд с трендом
3. Построим центрированную функцию прогнозируемой величины относительно тренда
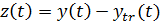 (2.11)
(2.11)
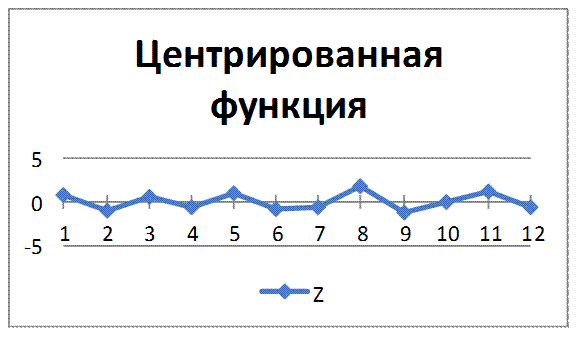 |
Рис 2.5 – Центрированная функция
4. Определим порядок модели (порядок задает количество лагов L), описывающей данный ряд:

где N – количество значений в исходной выборке.
5. Вычислим коэффициенты автокорреляции
Общая формула:
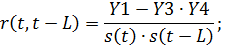
где:
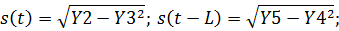
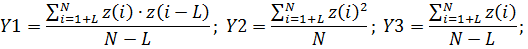
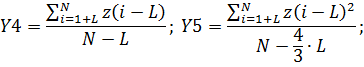
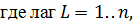
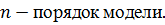
Для L = 1: 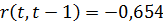 .
.
Для L = 2: 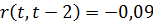 .
.
Для L = 3: 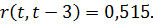
6. Определим прогнозирующую модель
Прогнозирующая модель имеет вид:
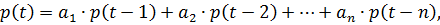
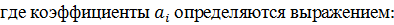
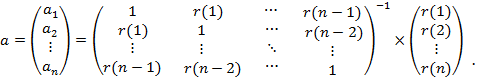
Определим размерность прогнозирующей модели, которая определяется номером лага L, при котором коэффициент автокорреляции по модулю становится не значимым, а при предыдущем лаге L-1, коэффициент автокорреляции был значимым. Например, рассмотрим таблицу 2.3.
Таблица 2.3 – Значимость коэффициента автокорреляции
| Лаг L (порядок) | 1 | 2 | 3 |
Коэффициент автокорреляции 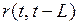
| -0,654 | -0,09 | 0,515 |
| Число степеней свободы (N-2-L) | 9 | 8 | 7 |
| Табличные значения коэффициента корреляции | 0,6021 | 0,6319 | 0,6664 |
| Значимость коэффициента автокорреляции | значим | не значим | не значим |
Так как при лаге L=2 коэффициент автокорреляции r(t, t-2) становится не значимым, то размерность прогнозирующей модели m=2, а в случае, если он был бы значимым, то размерность прогнозирующей модели была бы равна 3.
Определим коэффициенты прогнозирующей модели:
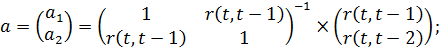
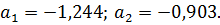

Прогнозирующая модель центрированных значений выходной величины запишется в виде:
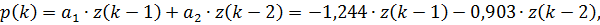
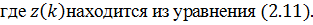
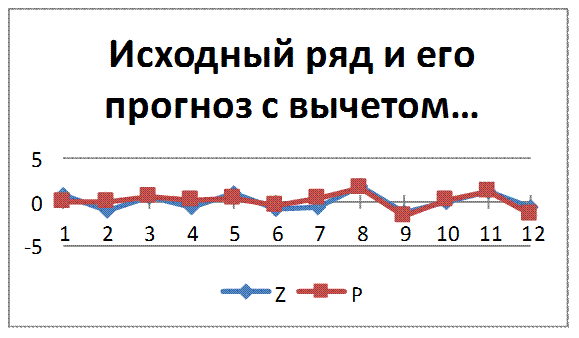
Рис. 2.6 – Исходный ряд и его прогноз с вычетом тренда
Прогноз выходной величины с учетом тренда запишется в виде:
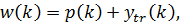
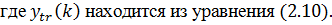
Рис. 2.7 – Исходный ряд и его прогноз с учетом 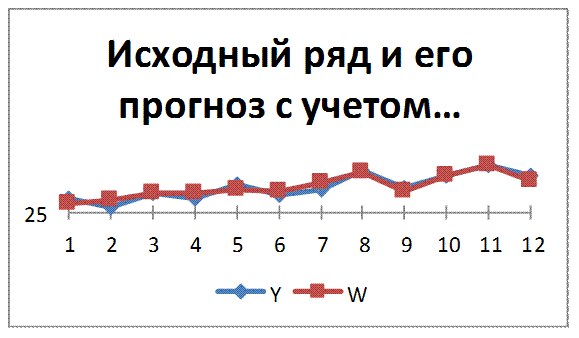
тренда
7. Прогноз выходной величины
Выполним прогноз значений временного ряда на основе полученной модели, последовательно подставляя значения z(t-k), k = 1…3 в модель (2.7)
Для прогноза на один шаг вперед прогнозирующая функция примет вид:
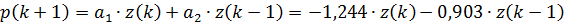
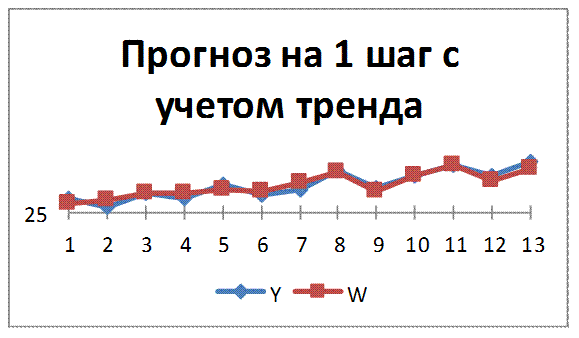
Рис. 2.8 – Прогноз на один шаг с учетом тренда
Вычислим дисперсию выходной величины
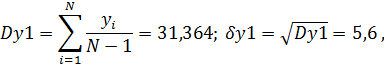
И дисперсию прогноза на один шаг вперед
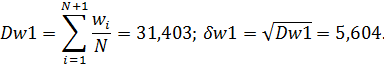
Для прогноза на один шаг вперед прогнозирующая функция примет вид:
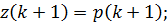
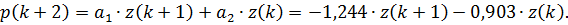
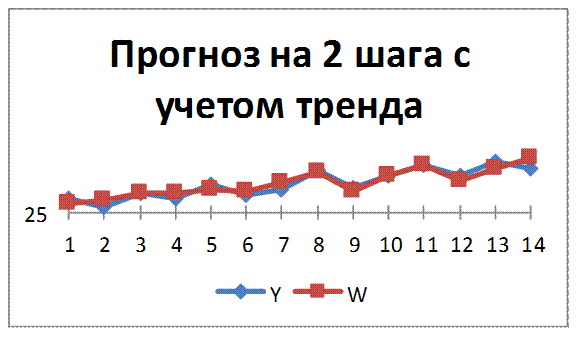
Рис. 2.9 – Прогноз на 2 шага с учетом тренда
Вычислим дисперсию выходной величины
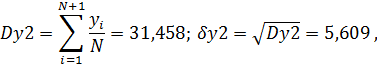
И дисперсию прогноза на два шага вперед
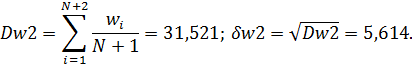
Для прогноза на один шаг вперед прогнозирующая функция примет вид:
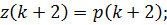
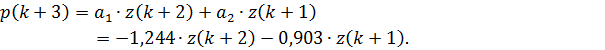

Рис 2.10 – Прогноз на 3 шага с учетом тренда
Вычислим дисперсию выходной величины
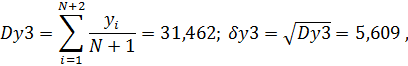
И дисперсию прогноза на два шага вперед
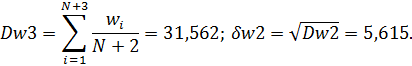
8. Вычисление дисперсии ошибки прогноза при разных значениях шага прогноза
Формула ошибки прогноза
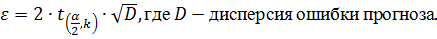
Найдем дисперсию ошибки прогноза при прогнозе на один шаг:

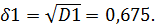
Ошибка прогноза на один шаг равна
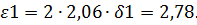
Найдем дисперсию ошибки прогноза при прогнозе на два шага:
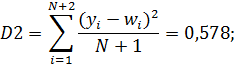
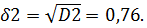
Ошибка прогноза на два шага равна:
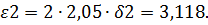
Найдем дисперсию ошибки прогноза при прогнозе на три шага:
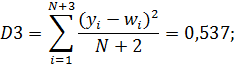
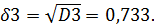
Ошибка прогноза на три шага:
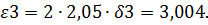
Таблица 2.4 – Сравнение дисперсий исходного ряда и его прогноза
|
| Прогноз на 1 шаг вперед | Прогноз на 2 шага вперед | Прогноз на 3 шага вперед | |
| Исходные данные | D | 31,364 | 31,458 | 31,462 |
| δ | 5,6 | 5,609 | 5,609 | |
| Прогноз | D | 31,403 | 31,521 | 31,562 |
| δ | 5,604 | 5,614 | 5,615 | |
Таблица 2.5 – Данные прогноза
| Прогноз на 1 шаг вперед | Прогноз на 2 шага вперед | Прогноз на 3 шага вперед | |
| Фактические данные | 32,5 | 31,5 | 31,6 |
| Данные прогноза | 31,39 | 32,93 | 31,59 |
Таблица 2.6 – Данные прогноза с учетом ошибки
| Прогноз на 1 шаг вперед | Прогноз на 2 шага вперед | Прогноз на 3 шага вперед | |
| D | 0,455 | 0,578 | 0,537 |
| δ | 0,675 | 0,76 | 0,733 |
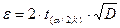
| 2,78 | 3,118 | 3,004 |
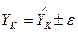
| 31,39 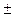 2,78 2,78
| 32,93 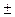 3,118 3,118
| 31,59 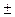 3,004 3,004
|
Вывод:
Оценим значимости различий между дисперсиями исходной величины и ее прогноза с помощью критерия Фишера:
1. Прогноз на 1 шаг
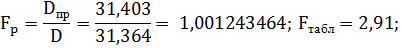
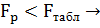 различие между дисперсиями с доверительной вероятностью 0,95 незначимо.
различие между дисперсиями с доверительной вероятностью 0,95 незначимо.
2. Прогноза на 2 шага
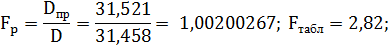
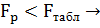 различие между дисперсиями с доверительной вероятностью 0,95 незначимо.
различие между дисперсиями с доверительной вероятностью 0,95 незначимо.
3. Прогноз на 3 шага
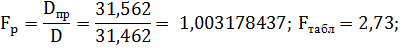
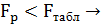 различие между дисперсиями с доверительной вероятностью 0,95 незначимо.
различие между дисперсиями с доверительной вероятностью 0,95 незначимо.
Так как при всех шагах прогноза различия между дисперсиями прогнозируемого и исходного рядов с доверительной вероятностью 0,95 статистически незначимы, то эти дисперсии однородны. Отклонение прогноза от исходной величины с доверительной вероятностью 0,95 попадает в интервал [- 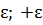 ], и
], и 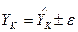 .
.
Содержание отчета
1. Формулировка задания
2. Исходные данные
3. Расчетно-графическая часть
4. Таблицы полученных данных
5. Вывод
 Таблица 2.7 – Исходные данные для выполнения расчетов
Таблица 2.7 – Исходные данные для выполнения расчетов
| Значения факторов | Значения выходных величин | |||||||||||||||||
| № | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 | Х9 | Х10 | Y1 | Y2 | Y3 | Y4 | Y5 | Y6 | Y7 | Y8 |
| 1 | 3,0 | 13,5 | 32,3 | 61,7 | 10,0 | 3,5 | 15,5 | 6,7 | 45,5 | 3,0 | 18,2 | 29,2 | 27,0 | 9,4 | 6,4 | 22,2 | 17,7 | 17,6 |
| 2 | 2,1 | 13,2 | 31,0 | 63,5 | 9,2 | 3,0 | 15,1 | 5,5 | 45,1 | 2,5 | 27,2 | 27,8 | 25,8 | 9,1 | 6,8 | 20,7 | 16,0 | 18,4 |
| 3 | 3,3 | 12,7 | 33,2 | 59,5 | 11,5 | 2,1 | 16,6 | 6,3 | 46,2 | 1,8 | 26,6 | 31,0 | 27,8 | 9,7 | 6,3 | 22,1 | 19,5 | 16,7 |
| 4 | 3,5 | 12,5 | 32,0 | 63,0 | 12,8 | 2,7 | 15,7 | 5,0 | 45,7 | 2,7 | 27,5 | 31,7 | 27,0 | 9,6 | 7,1 | 20,4 | 21,1 | 18,1 |
| 5 | 3,6 | 12,5 | 35,0 | 58,0 | 10,1 | 1,7 | 17,0 | 4,2 | 47,0 | 1,7 | 26,6 | 30,5 | 29,0 | 9,8 | 6,0 | 19,8 | 18,6 | 16,2 |
| 6 | 3,8 | 12,0 | 32,6 | 61,5 | 10,3 | 2,5 | 18,0 | 5,2 | 45,5 | 2,8 | 27,2 | 32,5 | 27,6 | 9,8 | 7,1 | 20,0 | 21,7 |  17,4 17,4
|
| 7 | 4,0 | 11,5 | 34,0 | 60,0 | 11,5 | 2,0 | 16,7 | 4,0 | 47,0 | 2,1 | 27,1 | 31,2 | 28,4 | 9,8 | 6,5 | 19,8 | 20,2 | 16,8 |
| 8 | 4,1 | 12,6 | 35,8 | 64,5 | 15,0 | 1,1 | 18,3 | 5,0 | 46,1 | 1,5 | 28,2 | 36,4 | 31,2 | 10,5 | 6,0 | 20,9 | 23,9 | 15,3 |
| 9 | 4,2 | 11,2 | 34,2 | 59,7 | 12,5 | 2,0 | 17,6 | 3,3 | 47,7 | 2,0 | 26,8 | 32,3 | 28,5 | 9,9 | 6,6 | 19,5 | 21,4 | 16,5 |
| 10 | 4,5 | 11,0 | 36,5 | 55,2 | 15,0 | 1,5 | 19,2 | 4,0 | 46,8 | 0,8 | 26,3 | 36,0 | 30,3 | 10,2 | 6,6 | 20,2 | 24,2 | 15,3 |
| 11 | 4,5 | 10,6 | 38,0 | 53,7 | 16,2 | 0,8 | 18,0 | 2,7 | 48,3 | 1,6 | 26,2 | 38,0 | 31,9 | 10,9 | 6,0 | 19,2 | 25,8 | 14,4 |
| 12 | 4,7 | 10,2 | 35,7 | 52,6 | 14,0 | 0,5 | 19,7 | 3,2 | 47,5 | 0,8 | 25,5 | 34,6 | 30,5 | 10,8 | 5,6 | 19,7 | 23,3 | 13,8 |
| 13 | 4,8 | 10,0 | 39,1 | 55,6 | 18,0 | 1,2 | 18,3 | 2,3 | 48,5 | 1,2 | 27,1 | 40,2 | 32,5 | 10,8 | 6,6 | 18,8 | 27,9 | 15,1 |
| 14 | 5,0 | 9,5 | 36,3 | 55,0 | 16,0 | 0,3 | 20,5 | 2,8 | 48,0 | 0,2 | 26,4 | 36,8 | 31,5 | 11,4 | 5,7 | 19,5 | 25,5 | 14,0 |
| 15 | 5,0 | 9,2 | 37,2 | 52,5 | 18,5 | 0,7 | 20,0 | 1,5 | 49,2 | 0,5 | 25,9 | 39,8 | 31,6 | 11,1 | 6,5 | 18,2 | 28,3 | 14,1 |
Таблица 2.8 – Варианты заданий
| Номер варианта | Используемые переменные | |||
| 1 | Y2 | X2 | X3 | X4 |
| 2 | Y2 | X3 | X4 | X5 |
| 3 | Y2 | X2 | X4 | X5 |
| 4 | Y2 | X2 | X3 | X5 |
| 5 | Y3 | X3 | X4 | X5 |
| 6 | Y3 | X4 | X5 | X6 |
| 7 | Y3 | X3 | X5 | X6 |
| 8 | Y3 | X3 | X4 | X6 |
| 9 | Y4 | X4 | X5 | X6 |
| 10 | Y4 | X5 | X6 | X7 |
| 11 | Y4 | X4 | X6 | X7 |
| 12 | Y4 | X4 | X5 | X7 |
| 13 | Y5 | X5 | X7 | X8 |
| 14 | Y5 | X8 | X5 | X6 |
| 15 | Y5 | X5 | X6 | X7 |
| 16 | Y5 | X6 | X7 | X8 |
| 17 | Y6 | X6 | X7 | X8 |
| 18 | Y6 | X7 | X8 | X9 |
| 19 | Y6 | X6 | X8 | X9 |
| 20 | Y6 | X6 | X7 | X3 |
| 21 | Y7 | X1 | X3 | X5 |
| 22 | Y7 | X3 | X5 | X7 |
| 23 | Y7 | X1 | X5 | X7 |
| 24 | Y7 | X1 | X3 | X7 |
| 25 | Y8 | X2 | X4 | X6 |
| 26 | Y8 | X3 | X7 | X9 |
| 27 | Y8 | X2 | X3 | X4 |
| 28 | Y8 | X2 | X5 | X6 |
| 29 | Y8 | X3 | X5 | X7 |
| 30 | Y8 | X1 | X3 | X9 |
Дата добавления: 2020-04-25; просмотров: 273; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
