Мысал. Граф К5 гамильтонды так как , например цикл 1, 2, 3, 4, 5 – гамильтон
Дирихле ережесі. Мысалдар.
22. Жиындар алгебрасының тепе-теңдіктері.
23. Жиындар. Жиынға қолданылатын амалдар.
24. Көбейту ережесі.
25. Кіріс және шығыс формуласы.
26. Қайшылық түсінігі. Логикалық эквивалентті формулалар. Логикалық эквиваленттіліктер.
27. Қалындылар класстары. Мысалдар. Қалдықтар туралы қытай теоремасы.
28. Қатынастар.
29. Қосу ережесі.
30. Математикалық индукция әдісі.
31. Мебиус функциясының анықтамасы. Мебиус функциясының мультипликативті болатынын дәлелдеу.
32. Мультипликативті функцияның анықтамасы. Мультипликативті функциялардың қасиеттерін дәлелдеу.
33. Өрнектелмейтін және құрама сандар.
34. Пікірлер логикасының тілі. Пікірлер логикасының формулалары және ақиқаттық кестелері.
Рассел парадоксы.
36. Рекуренттік қатынастар.
37. Реттік қатынастар.
38. Тавтология түсінігі. Тавтологияға қатысты қасиеттерді дәлелдеу.
39. Терулер. Орналастырулар. Биномиалдық коэфициенттер.
40. Тудындатушы функциялардың қасиеттері.
41. Тудындатушы функцияның анықтамасы. Мысалдар.
42. Үздіксіз бөлшектер. Жақындайтын бөлшектер.Қасиеттері.
Функциялар.
44. Эйлер функциясының анықтамасы. Эйлер функциясының мультипликативті болатынын дәлелдеу.
|
|
|
45. Эйлерлік графтар. Қасиеттер. Мысалдар.
Эратосфен елегі.
1. Ағаштар. Қасиеттер. Мысалдар.
Анықтама 1 . Циклі жоқ граф (ациклдік граф) орман деп аталады.
Анықтама 2. Ациклдік байланған граф ағаш деп аталады.
Теорема 3
( 𝑛 , 𝑚 ) -G графы үшін келесі тұжырымдар эквивалентті:
1) G - ағаш;
2) G - байланған граф және 𝑚 = 𝑛 – 1 ;
3) G - ациклді граф және 𝑚 = 𝑛 – 1 ;
4) G графының кез-келген беттеспейтін екі төбесін жалғыз жай тізбек байланыстырады.
Дәлелдеуі:
1)⇒ 2) Байланған және ациклдік ( 𝑛 , 𝑚 ) - G графы берілсін. n бойынша индукциямен 𝑚 = 𝑛 – 1 болатынын дәлелдейік.
Индукция базисі: 𝑛 = 1, 𝑚 = 0 ;
Индуктивті болжам: 𝑛 < 𝑘 болғанда, 𝑚 = 𝑛 − 1 болсын; Индуктивті көшу: 𝑛 = 𝑘 болғанда, 𝑚 = 𝑛 − 1 болатынын дәлелдейік.
Бір қабырғаны алып тастап, төбелерінің саны 
болатын екі ағаш аламыз. 
болатыны анық. Индуктивті болжам 
бойынша Қабырғаны қайтарып,
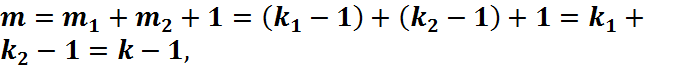аламыз.
2)⇒ 3) Байланған (n, m)- G графы берілсін және 𝑚 = 𝑛 – 1 болсын. G – ациклдік граф екенін дәлелдейік.
|
|
|
Кері жориық: G графында цикл болсын және осы циклдың қабырғасы
болсын. Онда 
(бұл граф G графынан e қабырғасын алып тастау арқылы шыққан граф) графы алдыңғы параграфтағы 7-ші теорема бойынша байланған болады және n -2 қабырғасы бар, ал бұл алдыңғы параграфтың 9- шы теоремасы бойынша мүмкін емес. Сондықтан G графы – ациклдік.
3)⇒ 4) Ациклдік ( 𝑛 , 𝑚 ) - G графы берілсін және 𝑚 = 𝑛 – 1 болсын.
G графының кез-келген екі төбесінің жалғыз жай тізбекпен байланысқанын дәлелдейік.
Кері жориық: кем дегенде екі u x1 x2 … xk v және u y1 y2 … ys v жай тізбектерімен қосуға болатын u және v төбелері болсын дейік. Бірақ ол кезде графта 3) пунктке қайшы келетін u x1 x2 … xk v ys … y1 y2 u екі циклі болады. Олай болса G графының кез-келген екі төбесі жалғыз жай тізбекпен байланысқан.
4)⇒ 1) G графының кез-келген екі төбесі жай тізбекпен (цепь) байланысқан. Олай болса, G графы байланған болады. G графында циклдің жоқ екендігін көрсетейік.
Кері жориық: G графында цикл болсын дейік. Онда осы циклдің кез-келген екі төбесін 4) пунктке қайшы келетін кем дегенде екі түрлі жай тізбектермен қосуға болады. Сондықтан, G графы ациклдік болады.
|
|
|
Теорема 4
Кез-келген n ретті ағашта кем дегенде екі ілінген төбесі болады.
Анықтама 5
Ағаштың ілінген төбесі соңғы төбесі деп аталады.
Теорема 6
Кез-келген ағаштың центрі бір немесе екі іргелес төбеден тұрады.
Анықтама 7
Графтың диаметрін құрайтын жай тізбек – диаметрлік тізбек деп аталады.
2.Ақырлы және ақырсыз жиындар. Мысалдар.
3.Ақырлы жиындарда анықталған инъекциялардың саны. 
4.Ақырлы жиындарда анықталған биекциялардың саны. . 
5. Ақырлы жиындарда анықталған сюръекциялардың саны.
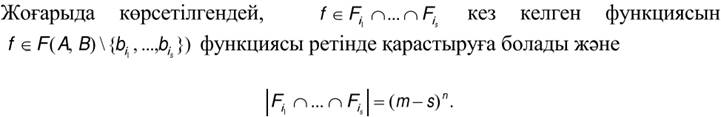
6.Арнайы бинарлы қатынастар. Бинарлы қатынастардың матрицасы 
7.Бинарлы қатынастар. Оларға қолданылатын амалдар.Мысалдар. Бинарлы қатынастардың қасиеттері.
8. Бөліктеу туралы теорема. Мысалдар. 
|
|
|
9. Гамильтондық графтар. Мысалдар 
Мысал. Граф К5 гамильтонды так как , например цикл 1, 2, 3, 4, 5 – гамильтон
10.Графтар түсінігі. Мысалдар 
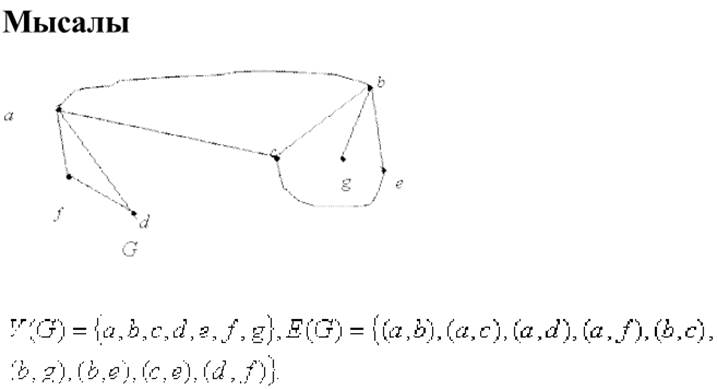
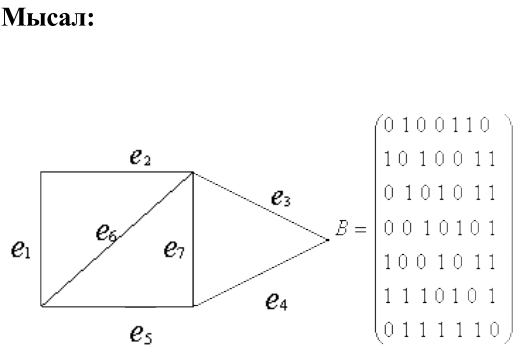
11.Графтарға қатысты матрицалар. 
Мысал 
13.Графтарға қолданатын амалдар. Мысалдар. 
\
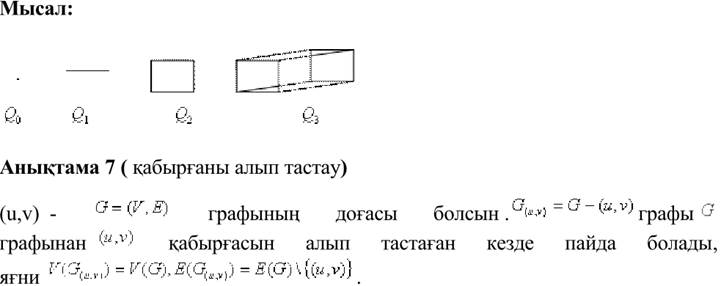
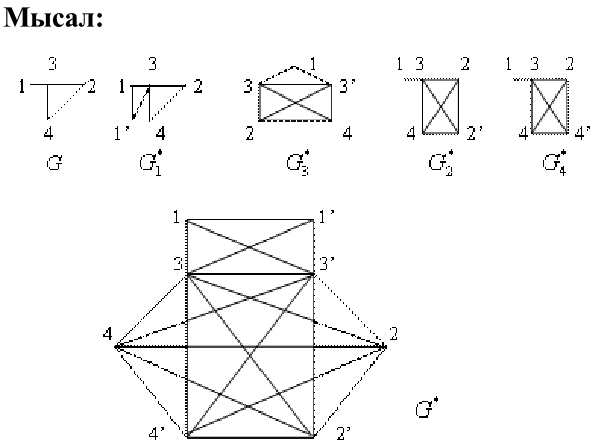
15.Графтардағы арақашықтық. Қасиеттер. 
16.Графтардың планарлығы. Мысалдар. 
17.Графтардың изоморфизмі. Мысалдар 
18.Графтардың хроматикалық саны. Мысалдар. 
19.Дизъюнктивті нормаланған формалар (ДНФ). Әрбір формулаға логикалық эквивалентті ДНФ табылатыны туралы теореманы дәлелдеу.
20.Диофанттық теңдеулер. Диофанттық теңдеулердің шешілу әдістері.
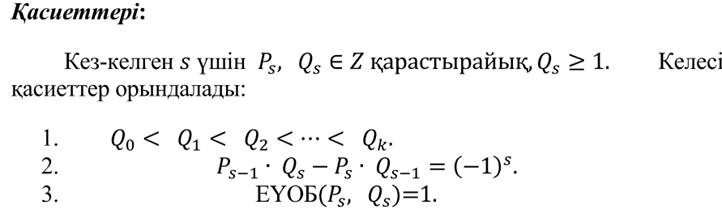
Дирихле ережесі. Мысалдар.
22.Жиындар алгебрасының тепе-теңдіктері.
23.Жиындар. Жиынға қолданылатын амалдар.
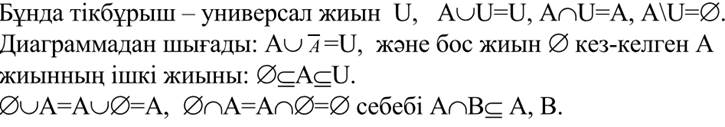
24.Көбейту ережесі.
25.Кіріс және шығыс формуласы.
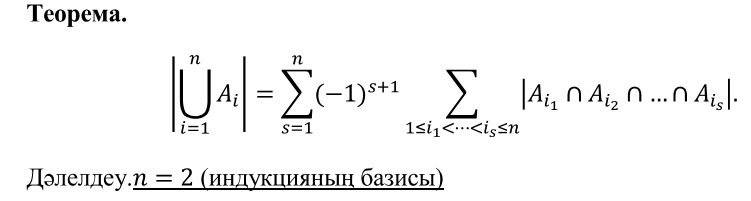
26.Қайшылық түсінігі. Логикалық эквивалентті формулалар. Логикалық эквиваленттіліктер. 
27.Қалындылар класстары. Мысалдар. Қалдықтар туралы қытай теоремасы. 
28.Қатынастар.
29.Қосу ережесі.
30.Математикалық индукция әдісі
31.Мебиус функциясының анықтамасы. Мебиус функциясының мультипликативті болатынын дәлелдеу.
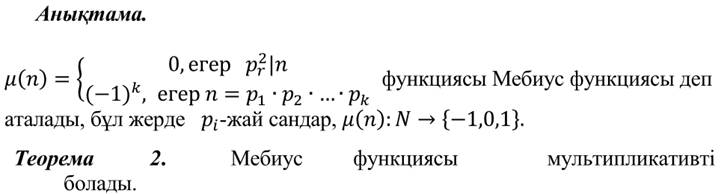
32.Мультипликативті функцияның анықтамасы. Мультипликативті функциялардың қасиеттерін дәлелдеу
33.Өрнектелмейтін және құрама сандар.
34.Пікірлер логикасының тілі. Пікірлер логикасының формулалары және ақиқаттық кестелері.
Рассел парадоксы.
36.Рекуренттік қатынастар.
37.Реттік қатынастар. 
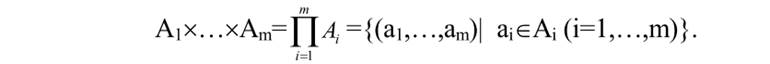
39.Терулер. Орналастырулар. Биномиалдық коэфициенттер.
41.Тудындатушы функцияның анықтамасы. Мысалдар.
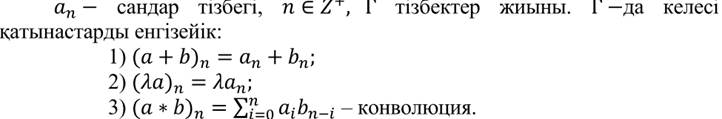
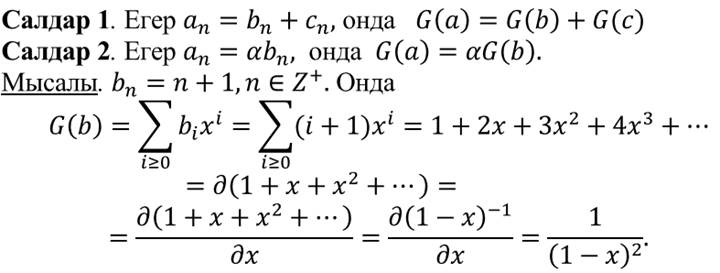
42.Үздіксіз бөлшектер. Жақындайтын бөлшектер.Қасиеттері.
Функциялар.
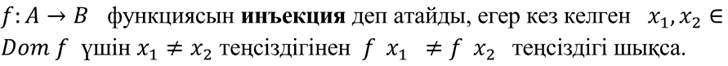
44.Эйлер функциясының анықтамасы. Эйлер функциясының мультипликативті болатынын дәлелдеу.
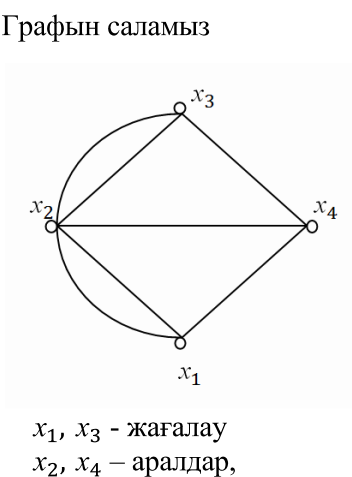
45.Эйлерлік графтар. Қасиеттер. Мысалдар.
Эратосфен елегі.
Дата добавления: 2020-04-08; просмотров: 668; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!